IB PHYSICS SL (Standard level)- 2024 – Practice Questions- All Topics
Topic 1 – Measurements and uncertainties
Topic 1 Weightage : 7 %
All Questions for Topic 1 Fundamental and derived SI units , Significant figures , Orders of magnitude, Estimation , Error bars , Uncertainty of gradient and intercepts
Question
A small ball of mass m is moving in a horizontal circle on the inside surface of a frictionless hemispherical bowl.
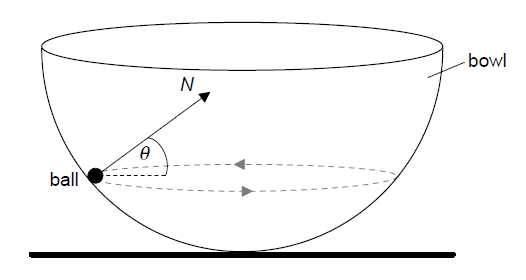
The normal reaction force N makes an angle θ to the horizontal.
State the direction of the resultant force on the ball.
On the diagram, construct an arrow of the correct length to represent the weight of the ball.
Show that the magnitude of the net force F on the ball is given by the following equation.
The radius of the bowl is 8.0 m and θ = 22°. Determine the speed of the ball.
Outline whether this ball can move on a horizontal circular path of radius equal to the radius of the bowl.
A second identical ball is placed at the bottom of the bowl and the first ball is displaced so that its height from the horizontal is equal to 8.0 m.
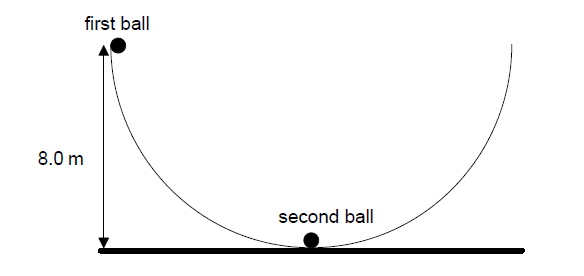
The first ball is released and eventually strikes the second ball. The two balls remain in contact. Determine, in m, the maximum height reached by the two balls.
Answer/Explanation
Markscheme
towards the centre «of the circle» / horizontally to the right
Do not accept towards the centre of the bowl
[1 mark]
downward vertical arrow of any length
arrow of correct length
Judge the length of the vertical arrow by eye. The construction lines are not required. A label is not required
[2 marks]
ALTERNATIVE 1
F = N cos θ
mg = N sin θ
dividing/substituting to get result
ALTERNATIVE 2
right angle triangle drawn with F, N and W/mg labelled
angle correctly labelled and arrows on forces in correct directions
correct use of trigonometry leading to the required relationship
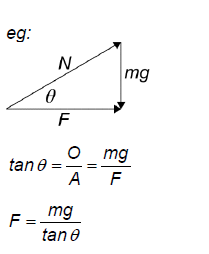

Award [4] for a bald correct answer
Award [3] for an answer of 13.9/14 «ms –1». MP2 omitted
[4 marks]
there is no force to balance the weight/N is horizontal
so no / it is not possible
Must see correct justification to award MP2
[2 marks]

Allow 12.5 from incorrect use of kinematics equations
Award [3] for a bald correct answer
Award [0] for mg(8) = 2mgh leading to h = 4 m if done in one step.
Allow ECF from MP1
Allow ECF from MP2
[3 marks]
Question
A glider is an aircraft with no engine. To be launched, a glider is uniformly accelerated from rest by a cable pulled by a motor that exerts a horizontal force on the glider throughout the launch.
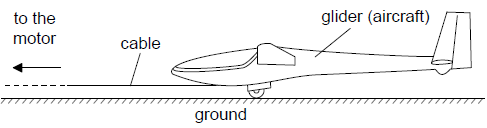
The glider reaches its launch speed of 27.0 m s–1 after accelerating for 11.0 s. Assume that the glider moves horizontally until it leaves the ground. Calculate the total distance travelled by the glider before it leaves the ground.
The glider and pilot have a total mass of 492 kg. During the acceleration the glider is subject to an average resistive force of 160 N. Determine the average tension in the cable as the glider accelerates.
The cable is pulled by an electric motor. The motor has an overall efficiency of 23 %. Determine the average power input to the motor.
The cable is wound onto a cylinder of diameter 1.2 m. Calculate the angular velocity of the cylinder at the instant when the glider has a speed of 27 m s–1. Include an appropriate unit for your answer.
After takeoff the cable is released and the unpowered glider moves horizontally at constant speed. The wings of the glider provide a lift force. The diagram shows the lift force acting on the glider and the direction of motion of the glider.
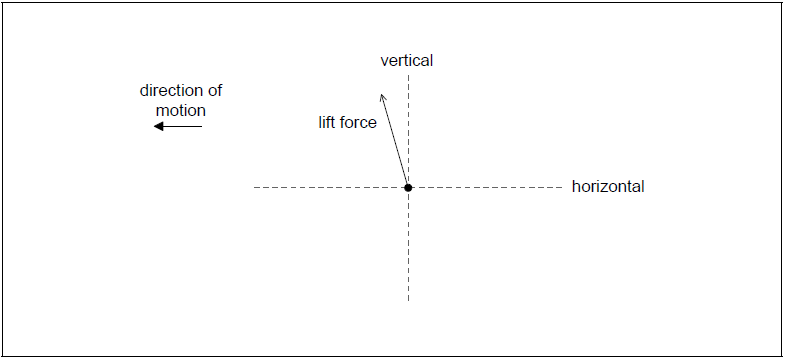
Draw the forces acting on the glider to complete the free-body diagram. The dotted lines show the horizontal and vertical directions.
Explain, using appropriate laws of motion, how the forces acting on the glider maintain it in level flight.
At a particular instant in the flight the glider is losing 1.00 m of vertical height for every 6.00 m that it goes forward horizontally. At this instant, the horizontal speed of the glider is 12.5 m s–1. Calculate the velocity of the glider. Give your answer to an appropriate number of significant figures.
