IB PHYSICS SL (Standard level)- 2024 – Practice Questions- All Topics
Topic 4.2 – Travelling Waves
Topic 4 Weightage : 10 %
All Questions for Topic 4.2 – Travelling waves , Wavelength, frequency, period and wave speed , Transverse and longitudinal waves , The nature of electromagnetic waves , The nature of sound waves
Question
A sound wave has a frequency of 1.0 kHz and a wavelength of 0.33 m. What is the distance travelled by the wave in 2.0 ms and the nature of the wave?
Distance travelled in 2.0 ms | Nature of the wave |
0.17 m | longitudinal |
0.17 m | transverse |
0.66 m | longitudinal |
0.66 m | transverse |
▶️Answer/Explanation
Ans: C
The speed of the sound, distance travelled and the time taken relationship is given as follows.
distance travelled = \(Speed \times time\)
Now for sound wave ,
\(v=n\lambda \) , \(\lambda \)= 0.33 m and \(n\) = 1k Hz
\(\therefore v= 10^3 \times 0.33 = 330 ms^{-1}\)
\(Distance \; travelled = 330 \times 2 \times 10^{-3} =0.66m\)
And Sound wave is longitudinal Wave.
Question
A sound wave has a wavelength of 0.20 m. What is the phase difference between two points along the wave which are 0.85 m apart?
A. zero
B. 45°
C. 90°
D. 180°
▶️Answer/Explanation
Markscheme
C
- Phase difference of 2π radian is equivalent to a path difference λ and a time difference of period T.
- Phase difference =
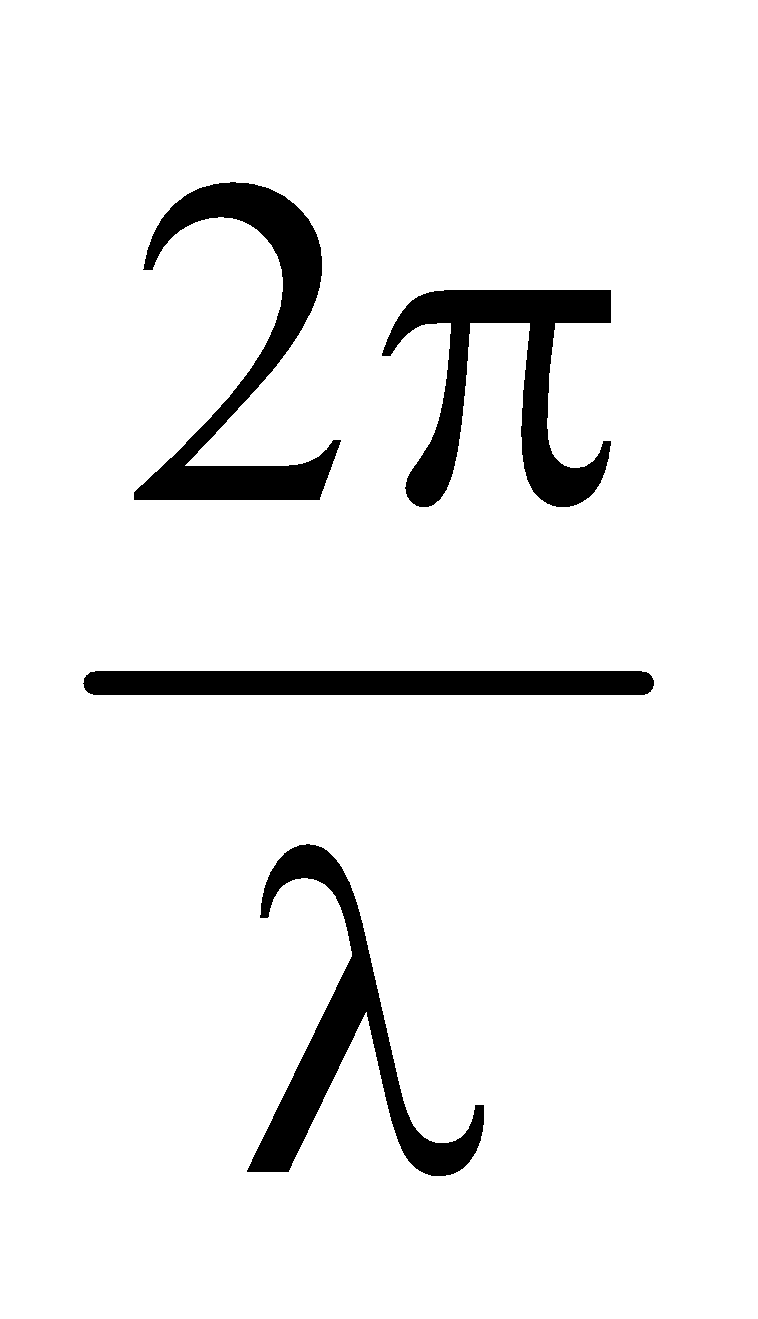× path difference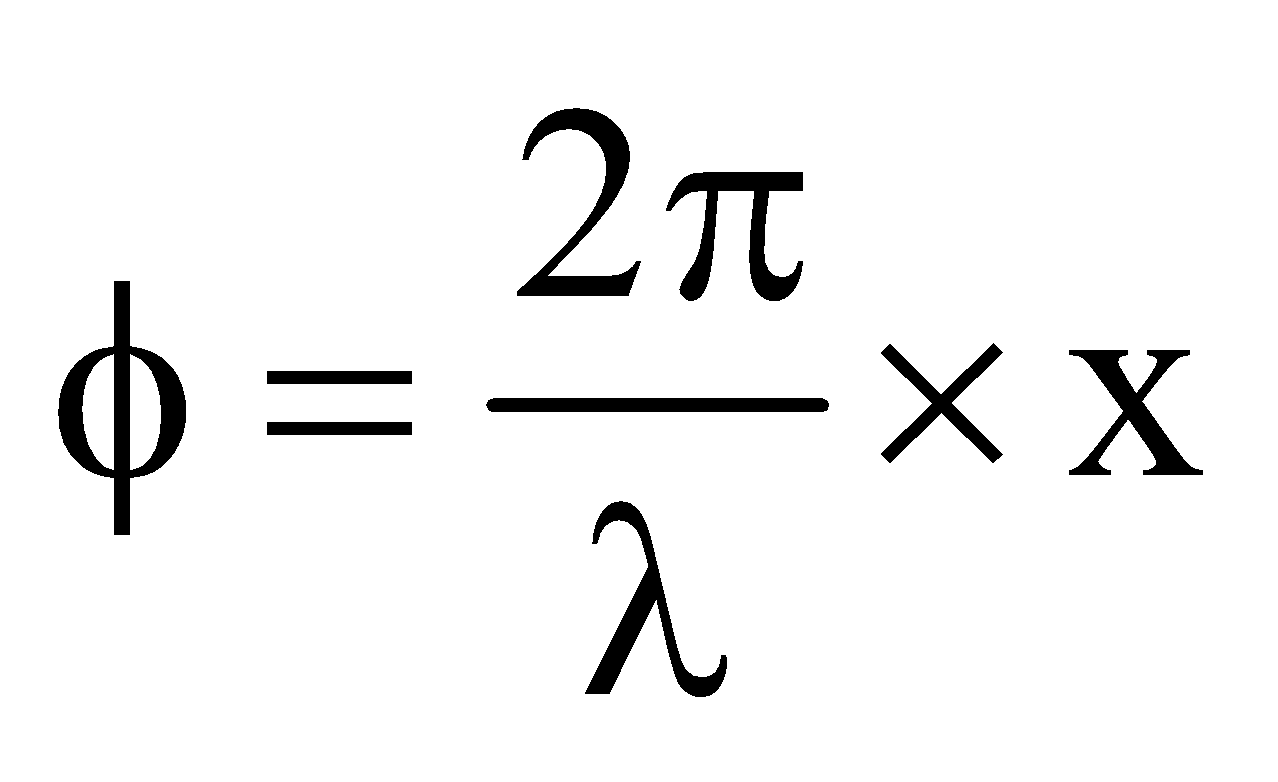 
Hence
\(\phi =\frac{2\pi}{\lambda }\times x\)
\(=\frac{2\pi}{0.2 }\times 0.85 =8.5 \pi =(2n+1)\frac{\pi}{2}=17\times \frac{\pi}{2}\)
After each 2 \(\pi\) cycle phase change become zero .
Hence phase difference \(\frac{\pi}{2}=90^{\circ}\)
Question
What is the phase difference, in rad, between the centre of a compression and the centre of a rarefaction for a longitudinal travelling wave?
A. 0
B. \(\frac{\pi }{2}\)
C. \(\pi \)
D. \(2\pi \)
▶️Answer/Explanation
Markscheme
C
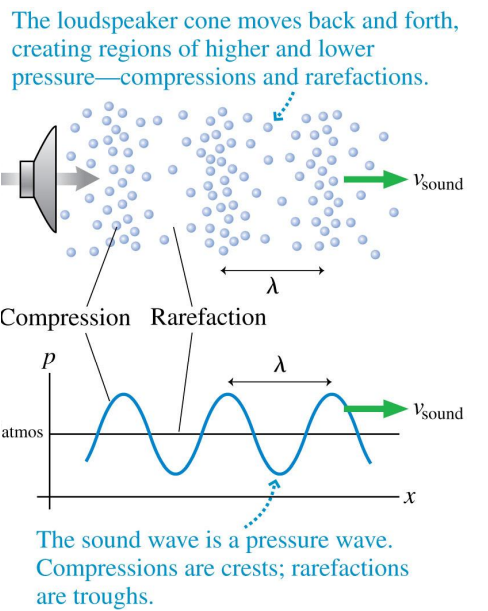
The distance between compression and the next rarefaction of a longitudinal wave is \(\frac{\lambda }{2}\) which is equivalent to \(\pi \) in terms of phase.
Question
The graph shows the variation with distance x of the displacement of the particles of a medium in which a longitudinal wave is travelling from left to right. Displacements to the right of equilibrium positions are positive.
Which point is at the centre of a compression?
- x = 0
- x = 1 m
- x = 2 m
- x = 3 m
▶️Answer/Explanation
Markscheme
B
The graph shows how the displacement of particles vary with distance from the source.
Points A, B, C and D are at specific distances from the source.
From the y-axis, the particles move away from the source when they have a positive value and they move towards the source when they have a negative value.
For a longitudinal wave, the direction of vibration is parallel to the direction of transfer of energy by the wave.
A compression occurs when the particles are close to each other. Let the centre of compression be X. If particles on the left of point X are moving towards the right (towards X), then particles on the right of point X would be moving towards the left (again, towards X). So, particles on each side of the centre of compression (X) are moving towards each other (and towards X).
From distance = 0 towards point A, the particles move away from the source as the displacement is positive.
From point A towards B, the displacement is still positive. So, the particles are still moving away from the source.
So, just before point B the particle is moving away from the source (towards B) as the displacement is positive, and just after point B it is moving towards the source (as the displacement is now negative) and also towards B (as the particle is returning on its path towards the source).
So, B must be the centre of a compression.
Point D is the centre of a rarefaction as just before D, the particles are moving towards the source (and away from D) since the displacement is negative. And just after D, the particles are moving away from the source (and away from D) since the displacement is now positive. So, the particles are moving away from each other and D is at the centre. This is rarefaction.
The other two points are midway between centres of compression and rarefaction.
Question
A girl in a stationary boat observes that 10 wave crests pass the boat every minute. What is the period of the water waves?
A. \(\frac{1}{10}\) min
B. \(\frac{1}{10}\) min–1
C. 10 min
D. 10 min–1
▶️Answer/Explanation
Markscheme
A
The period of a wave is the time for a particle on a medium to make one complete vibrational cycle
Parameters of water waves
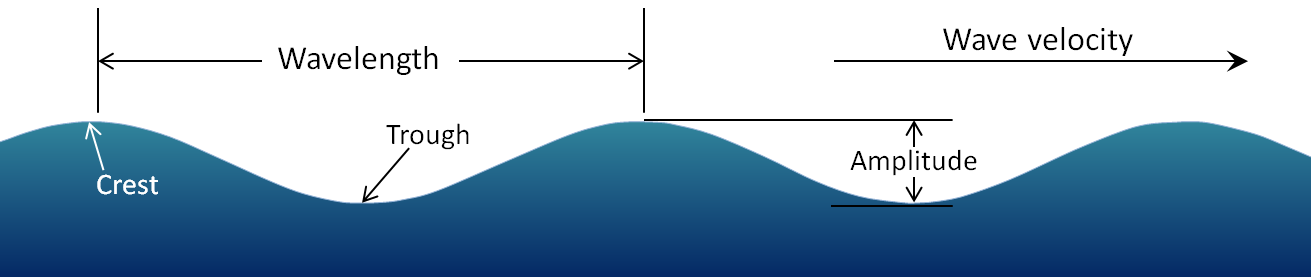
Crest to Crest is one Time period (T)
Hence \(10 \times T = 1\; min\)
or
\(T= \frac{1}{10}\; min\)
Question
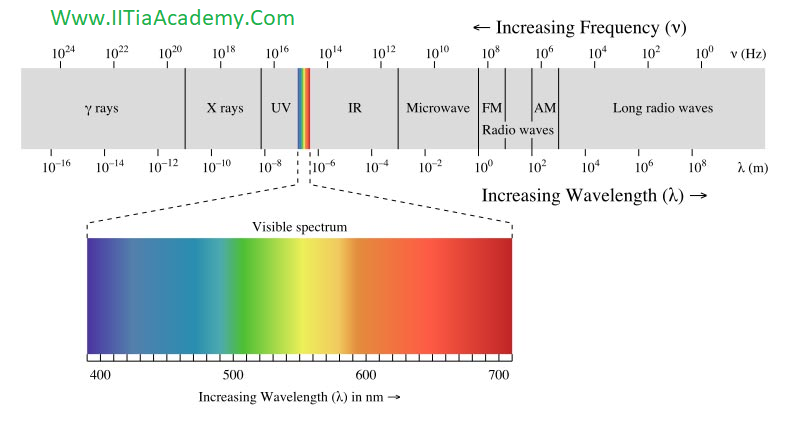
What statement about X-rays and ultraviolet radiation is correct?
A. X-rays travel faster in a vacuum than ultraviolet waves.
B. X-rays have a higher frequency than ultraviolet waves.
C. X-rays cannot be diffracted unlike ultraviolet waves.
D. Microwaves lie between X-rays and ultraviolet in the electromagnetic spectrum.
▶️Answer/Explanation
Markscheme
B
Ultraviolet light is located between X-radiation and visible light. UV has a higher frequency and shorter wavelength than visible light, and it has a lower frequency and longer wavelength than X-radiation. UV with its longer wavelength and less energy is less penetrating than X-ray and is sometimes absorbed by matter.
Electromagnetic Spectrum
Question
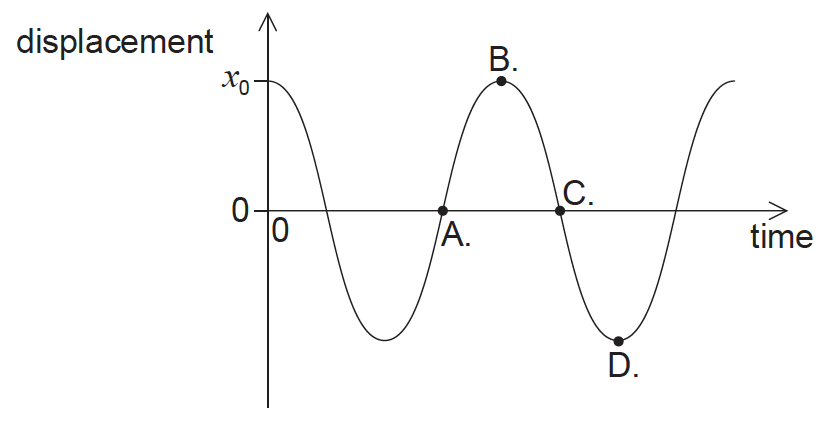
The bob of a pendulum has an initial displacement \(x\)0 to the right. The bob is released and allowed to oscillate. The graph shows how the displacement varies with time. At which point is the velocity of the bob at maximum towards the right?
▶️Answer/Explanation
Markscheme
A
Related Links