IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 5.1 Electric fields
Topic 5 Weightage : 5 %
All Questions for Topic 5.1 – Charge , Electric field , Coulomb’s law , Electric current , Direct current (dc) , Potential difference
Question
An electron is placed at a distance of 0.40 m from a fixed point charge of –6.0 mC.
(a) Show that the electric field strength due to the point charge at the position of the electron is 3.4 × 108 N C–1. [2]
(b) (i) Calculate the magnitude of the initial acceleration of the electron. [2]
(ii) Describe the subsequent motion of the electron
▶️Answer/Explanation
Ans:
a
E = \(\frac{k\times q}{r^2}\)
E = \(\frac{8.99\times 10^9\times 6.0\times 10^{-3}}{0.4^2}\) OR E = 3.37 × 10 8 «NC-1 »
b i
F = q ×E OR F = 1.6 ×10-19 × 3.4 ×108 = 5.4 × 10-11 « N»
a = « \(\frac{5.4\times 10^{-11}}{9.1\times 10^{-31}}\) » 5.9 × 1019 « ms-1»
b ii
the electron moves away from the point charge/to the right «along the line joining them» ✔
decreasing acceleration ✔
increasing speed ✔
Question
A vertical wall carries a uniform positive charge on its surface. This produces a uniform horizontal electric field perpendicular to the wall. A small, positively-charged ball is suspended in equilibrium from the vertical wall by a thread of negligible mas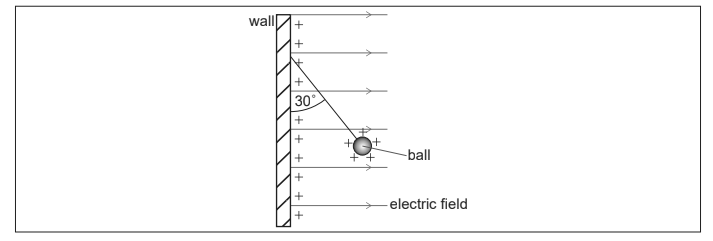 
(a) The charge per unit area on the surface of the wall is σ. It can be shown that the electric field strength E due to the charge on the wall is given by the equation
E =
Demonstrate that the units of the quantities in this equation are consistent. [2]
(b) (i) The thread makes an angle of 30° with the vertical wall. The ball has a mass of 0.025 kg. Determine the horizontal force that acts on the ball. [3]
(ii) The charge on the ball is 1.2 ×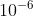 
C. Determine σ. [2]
(c) The thread breaks. Explain the initial subsequent motion of the ball. [3]
(d) The centre of the ball, still carrying a charge of 1.2 × 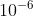C, is now placed 0.40 m from a point charge Q. The charge on the ball acts as a point charge at the centre of the ball. P is the point on the line joining the charges where the electric field strength is zero.
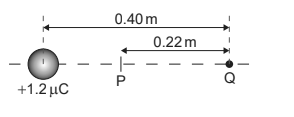
Calculate the charge on Q. State your answer to an appropriate number of significant figures. [3]
Outline, without calculation, whether or not the electric potential at P is zero. [2]
▶️Answer/Explanation
Ans:
a identifies units of σ as C m-2 seen and reduced to N C-1 Accept any analysis (eg dimensional) that yields answer correctly
b i horizontal force F on ball = T sin 30 T = F «=mg tan 30 = 0.025 x 9.8 x tan 30» = 0.14 «N» Allow g= 10 N kg -1 Award for a bald correct answer. Award for an answer of zero, interpreting that the horizontal force refers to the horizontal component of the net force.
b ii E= « » σ = «
» = 2.1 x 10-6 «C m-2» Allow ECF from the calculated F in (b)(i) Award [2] for a bald correct answer.
c horizontal/repulsive force and vertical force/pull of gravity act on the ball so ball has constant acceleration/constant net force motion is in a straight line at 30° to vertical away from wall/along original line of thread
d i «+»1.8 x 10-6 «C» ✓ 2sf Do not award MP2 if charge is negative Any answer given to 2 sig figs scores MP3
d ii work must be done to move a «positive» charge from infinity to P «as both charges are positive» OR reference to both potentials positive and added OR identifies field as gradient of potential and with zero value therefore, point P is at a positive / non-zero potential Award [0] for bald answer that P has non-zero potential
Related Links