IB PHYSICS HL(Higher level) – 2024 – Practice Questions- All Topics
Topic 5.2 Heating effect of electric currents
Topic 5 Weightage : 5%
All Questions for Topic 5.2 – Circuit diagrams , Kirchhoff’s circuit laws , Heating effect of current and its consequences , Resistance expressed as R = V/I , Ohm’s law , Resistivity , Power dissipation
Question
Three identical light bulbs, X, Y and Z, each of resistance 4.0Ω are connected to a cell of emf 12 V. The cell has negligible internal resistance.
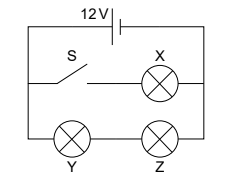
The switch S is initially open. Calculate the total power dissipated in the circuit. [2]
The switch is now closed.
State, without calculation, why the current in the cell will increase. [1]
Deduce the ratio

The cell is used to charge a parallel-plate capacitor in a vacuum. The fully charged capacitor is then connected to an ideal voltmeter.
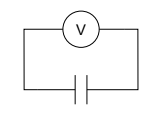
The capacitance of the capacitor is 6.0 μF and the reading of the voltmeter is 12 V.
Calculate the energy stored in the capacitor. [1]
When fully charged the space between the plates of the capacitor is filled with a dielectric with double the permittivity of a vacuum.
Calculate the change in the energy stored in the capacitor. [3]
Suggest, in terms of conservation of energy, the cause for the above change. [1]
▶️Answer/Explanation
Ans:
a
total resistance of circuit is 8.0 «Ω»
P = \(\frac{12^2}{8.0}\) = 18 «W»
b i
«a resistor is now connected in parallel» reducing the total resistance
OR
current through YZ unchanged and additional current flows through X ✔
b ii
evidence in calculation or statement that pd across Y/current in Y is the same as before ✔
so ratio is 1 ✔
c E = « \(\frac{1}{2}\) CV2 = \(\frac{1}{2}\) × 6 × 10-6 ×122 =»4.3 × 10-4 «J»
d i
ALTERNATIVE 1
capacitance doubles and voltage halves since E = \(\frac{1}{2}\) CV2 energy halves
so change is «-» 2.2 ×10-4 «J»
ALTERNATIVE 2
E = \(\frac{1}{2}\) CV2 and Q CV = so E = \(\frac{Q^2}{2C}\)
capacitance doubles and charge unchanged so energy halves
so change is «-» 2.2 × 10-4 «J»
d ii it is the work done when inserting the dielectric into the capacitor
Question
The graph shows how current I varies with potential difference V across a component X.
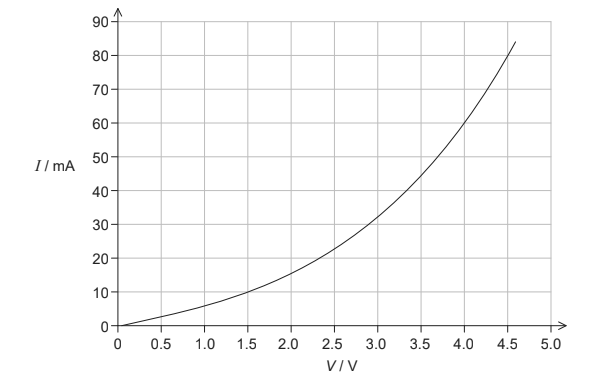
(a) Outline why component X is considered non-ohmic. [1]
(b) Component X and a cell of negligible internal resistance are placed in a circuit.
A variable resistor R is connected in series with component X. The ammeter reads 20 mA.
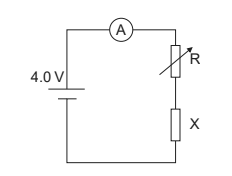
(i) Determine the resistance of the variable resistor. [3]
(ii) Calculate the power dissipated in the circuit. [1]
(c) Component X and the cell are now placed in a potential divider circuit.
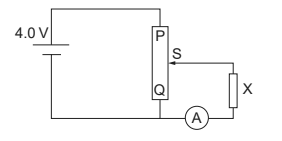
(i) State the range of current that the ammeter can measure as the slider S of the potential divider is moved from Q to P. [1]
(ii) Slider S of the potential divider is positioned so that the ammeter reads 20 mA.
Explain, without further calculation, any difference in the power transferred by the potential divider arrangement over the arrangement in (b). [3]
▶️Answer/Explanation
Ans:
a
current is not «directly» proportional to the potential difference
OR
resistance of X is not constant
OR
resistance of X changes «with current/voltage» ✓
b i
ALTERNATIVE 1
voltage across X = 2.3 «V»
voltage across R « = 4.0 – 2.3 » = 1.7 «V»
resistance of variable resistor « = \(\frac{1.7}{0.020}\) »= 85 « \(\Omega\) »
ALTERNATIVE 2
overall resistance « = \(\frac{4.0}{0.020}\) =200 Ω
resistance of X « = \(\frac{2.3}{0.020}\) »= 115 « \(\Omega\) »
resistance of variable resistor « = 200 – 115 »= 85 «\(\Omega\) »
b ii power «= 4.0 × 0.020 » = 0.080 «W»
c i from 0 to 60 mA
c ii
ALTERNATIVE 1
current from the cell is greater «than 20 mA» ✓
because some of the current must flow through section SQ of the potentiometer ✓
overall power greater «than in part (b)» ✓
ALTERNATIVE 2
total/overall resistance decreases ✓
because SQ and X are in parallel ✓
overall power greater «than in part (b)» ✓
