The equipment shown in the diagram was used by a student to investigate the variation with volume, of the pressure p of air, at constant temperature. The air was trapped in a tube of constant cross-sectional area above a column of oil.
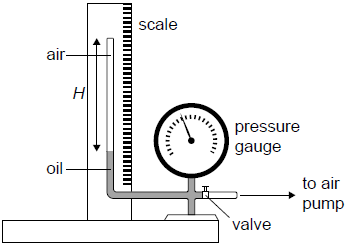
The pump forces oil to move up the tube decreasing the volume of the trapped air.
aThe student measured the height H of the air column and the corresponding air pressure p. After each reduction in the volume the student waited for some time before measuring the pressure. Outline why this was necessary.[1]
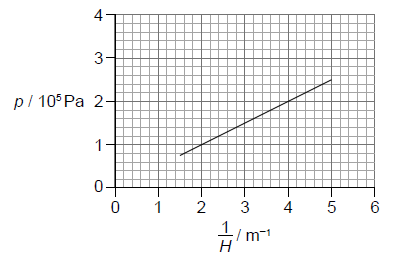
The equation of the line of best fit is \(p = a + \frac{b}{H}\).
Determine the value of b including an appropriate unit.[3]
▶️Answer/Explanation
Markscheme
a
in order to keep the temperature constant
in order to allow the system to reach thermal equilibrium with the surroundings/OWTTE
Accept answers in terms of pressure or volume changes only if clearly related to reaching thermal equilibrium with the surroundings.
[1 mark]
recognizes b as gradient
calculates b in range 4.7 × 104 to 5.3 × 104
Pa\(\,\)m
Award [2 max] if POT error in b.
Allow any correct SI unit, eg kg\(\,\)s–2.
[3 marks]
\(V \propto H\) thus ideal gas law gives \(p \propto \frac{1}{H}\)
so graph should be «a straight line through origin,» as observed
[2 marks]
\(n = \frac{{bA}}{{RT}}\) OR correct substitution of one point from the graph
\(n = \frac{{5 \times {{10}^4} \times 1.3 \times {{10}^{ – 3}}}}{{8.31 \times 300}} = 0.026 \approx 0.03\)
Answer must be to 1 or 2 SF.
Allow ECF from (b).
[2 marks]
very large \(\frac{1}{H}\) means very small volumes / very high pressures
at very small volumes the ideal gas does not apply
OR
at very small volumes some of the assumptions of the kinetic theory of gases do not hold
[2 marks]
In an experiment, data were collected on the variation of specific heat capacity of water with temperature. The graph of the plotted data is shown.
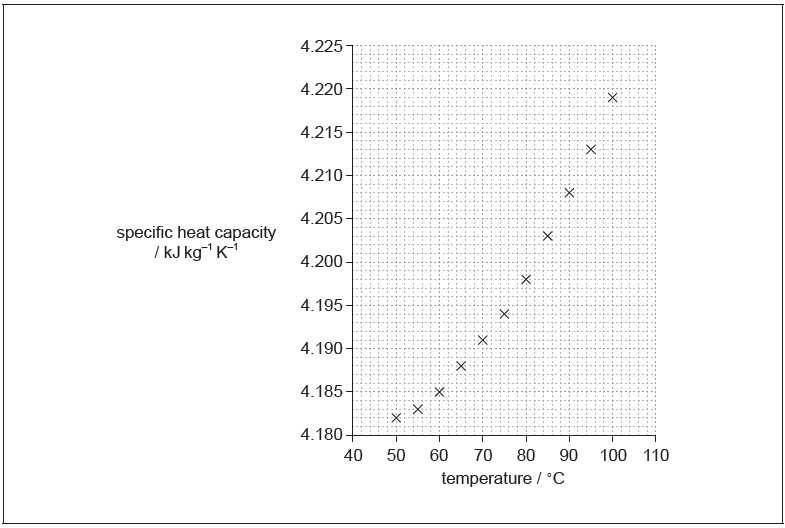
The uncertainty in the values for specific heat capacity is 5%.
Water of mass (100 ± 2) g is heated from (75.0 ± 0.5) °C to (85.0 ± 0.5) °C.
a.Draw the line of best-fit for the data.[1]
▶️Answer/Explanation
Markscheme
a.
single smooth curve passing through all data points
Do not accept straight lines joining the dots
Curve must touch some part of every x
tangent drawn at 80 °C
gradient values separated by minimum of 20 °C
9.0 × 10–4 «kJ kg–1 K–2»
Do not accept tangent unless “ruler” straight.
Tangent line must be touching the curve drawn for MP1 to be awarded.
Accept values between 7.0 × 10–4 and 10 × 10–4.
Accept working in J, giving 0.7 to 1.0
kJ kg−1 K−2
Accept J instead of kJ
Accept °C–2 instead of K−2
Accept °C–1 K–1 instead of K−2
Accept C for °C
«0.1 x 4.198 x 10 =» 4.198 «kJ» or 4198 «J»
Accept values between 4.19 and 4.21
percentage uncertainty in ΔT = 10%
«2% + 5% + 10%» = 17%
absolute uncertainty «0.17 × 4.198 =» 0.7 «kJ» therefore 2 sig figs
OR
absolute uncertainty to more than 1 sig fig and consistent final answer
Allow fractional uncertainties in MP1 and MP2
Watch for ECF from (c)(i)
Watch for ECF from MP1
Watch for ECF from MP2
Do not accept an answer without justification
