IBDP Maths AHL 5.19 Maclaurin series AA HL Paper 1- Exam Style Questions- New Syllabus
Question
(ii) Hence or otherwise, find $\lim_{x \to 0} \frac{f_n(x) – 1}{x^2}$ in terms of $n$.
Most-appropriate topic codes (IB Mathematics Analysis and Approaches 2021):
AHL 5.11: Definite integrals and reduction concepts — parts (a), (b)
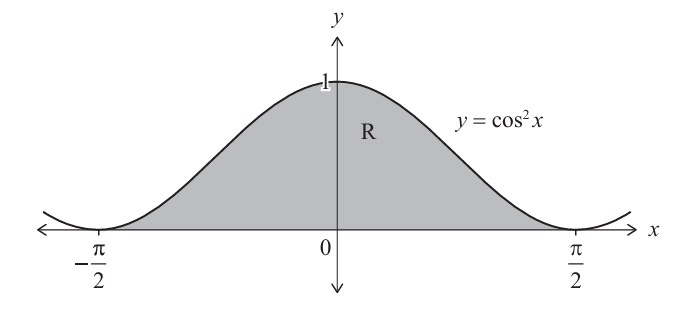
AHL 5.17: Volumes of revolution— part (d)
AHL 5.19: Maclaurin series — part (e)(i)
AHL 5.13: L’Hôpital’s rule and limits— part (e)(ii)
▶️ Answer/Explanation
(a) Integration by parts:
Let \( u = \cos^{n-1}x \), \( dv = \cos x dx \)
Then \( du = -(n-1)\cos^{n-2}x \sin x dx \), \( v = \sin x \)
\(\int \cos^n x dx = \cos^{n-1}x \sin x – \int \sin x \cdot [-(n-1)\cos^{n-2}x \sin x] dx \)
\( = \cos^{n-1}x \sin x + (n-1) \int \cos^{n-2}x \sin^2 x dx \)
Since \( \sin^2 x = 1 – \cos^2 x \):
\( = \cos^{n-1}x \sin x + (n-1) \int \cos^{n-2}x (1 – \cos^2 x) dx \)
\( = \cos^{n-1}x \sin x + (n-1) \int \cos^{n-2}x dx – (n-1) \int \cos^n x dx \)
(b) Rearranging:
From (a): \( \int \cos^n x dx = \cos^{n-1}x \sin x + (n-1) \int \cos^{n-2}x dx – (n-1) \int \cos^n x dx \)
Bring \( (n-1) \int \cos^n x dx \) to LHS:
\( \int \cos^n x dx + (n-1) \int \cos^n x dx = \cos^{n-1}x \sin x + (n-1) \int \cos^{n-2}x dx \)
\( n \int \cos^n x dx = \cos^{n-1}x \sin x + (n-1) \int \cos^{n-2}x dx \)
Divide by \( n \):
\( \int f_n(x) dx = \frac{1}{n} \cos^{n-1}x \sin x + \frac{n-1}{n} \int f_{n-2}(x) dx \)
(c) Applying reduction formula for \( n = 4 \):
\( \int \cos^4 x dx = \frac{1}{4} \cos^3 x \sin x + \frac{3}{4} \int \cos^2 x dx \)
For \( \int \cos^2 x dx \), use formula with \( n = 2 \):
\( \int \cos^2 x dx = \frac{1}{2} \cos x \sin x + \frac{1}{2} \int 1 dx = \frac{1}{2} \cos x \sin x + \frac{1}{2} x \)
Thus:
\( \int \cos^4 x dx = \frac{1}{4} \cos^3 x \sin x + \frac{3}{4} \left( \frac{1}{2} \cos x \sin x + \frac{1}{2} x \right) \)
\( = \frac{1}{4} \cos^3 x \sin x + \frac{3}{8} \cos x \sin x + \frac{3}{8} x + c \)
So \( p = \frac{1}{4}, q = \frac{3}{8}, r = \frac{3}{8} \).
(d) Volume of revolution:
Volume = \( \pi \int_{-\pi/2}^{\pi/2} (\cos^2 x)^2 dx = \pi \int_{-\pi/2}^{\pi/2} \cos^4 x dx \)
Using part (c) without constant:
\( \int_{-\pi/2}^{\pi/2} \cos^4 x dx = \left[ \frac{1}{4} \cos^3 x \sin x + \frac{3}{8} \cos x \sin x + \frac{3}{8} x \right]_{-\pi/2}^{\pi/2} \)
At \( x = \pi/2 \): \( \sin(\pi/2) = 1, \cos(\pi/2) = 0 \) → first two terms zero, value = \( \frac{3}{8} \cdot \frac{\pi}{2} = \frac{3\pi}{16} \)
At \( x = -\pi/2 \): \( \sin(-\pi/2) = -1, \cos(-\pi/2) = 0 \) → first two terms zero, value = \( \frac{3}{8} \cdot (-\frac{\pi}{2}) = -\frac{3\pi}{16} \)
Subtract: \( \frac{3\pi}{16} – (-\frac{3\pi}{16}) = \frac{3\pi}{8} \)
Volume = \( \pi \cdot \frac{3\pi}{8} = \frac{3\pi^2}{8} \)
(e)(i) Maclaurin series:
\( \cos x = 1 – \frac{x^2}{2} + O(x^4) \)
\( f_n(x) = (1 – \frac{x^2}{2} + \dots)^n \)
Up to \( x^2 \) term: \( f_n(x) \approx 1 – \frac{n x^2}{2} \)
Thus: \( f_n(x) = 1 – \frac{n x^2}{2} + O(x^4) \)
(e)(ii) Limit:
\( \lim_{x \to 0} \frac{\cos^n x – 1}{x^2} = \lim_{x \to 0} \frac{1 – \frac{n x^2}{2} – 1 + O(x^4)}{x^2} \)
\( = \lim_{x \to 0} \left( -\frac{n}{2} + O(x^2) \right) = -\frac{n}{2} \)