Question
A particle moves in a straight line. The velocity, v ms–1 , of the particle at time t seconds is given by v (t) = t sint – 3 , for 0 ≤ t ≤ 10.
The following diagram shows the graph of v .
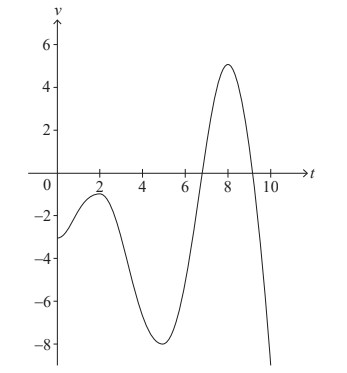
Find the smallest value of t for which the particle is at rest. [2]
Find the total distance travelled by the particle. [2]
Find the acceleration of the particle when t = 7 . [2]
▶️Answer/Explanation
Ans:
(a) recognising v=o t = 6.74416… = 6.74 (sec)
 = 37.0968… = 37.1 (m)
= 37.0968… = 37.1 (m)
(c) recognising acceleration at t = 7 is given by v’ (7) acceleration = 5.93430… = 5.93 (ms-2)
Question
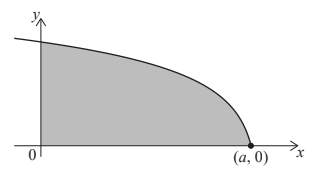
Let f (x) = \(\sqrt{12-2x}\) , x ≤ a . The following diagram shows part of the graph of f .
The shaded region is enclosed by the graph of f , the x-axis and the y-axis.
 x
x
The graph of f intersects the x-axis at the point (a , 0) .
Find the value of a . [2]
Find the volume of the solid formed when the shaded region is revolved 360° about the x-axis. [5]
▶️Answer/Explanation
Ans:
(a)
recognize f (x) = 0
eg \(\sqrt{12-2x}= 0, 2x=12\)
a= 6 (accept x= 6, (6,0))
(b)
attempt to substitute either their limits or the function into volume formula (must involve \(f^{2})\)
eg \(\int_{0}^{6}f^{2}dx , \pi \int (\sqrt{12-2x})^{2}, \pi \int_{0}^{6}\)(12-2x) dx
correct integaration of each term
eg \(12x-x^{2}, 12x-x^{2}\)+c, \(\left [ 12x-x^{2} \right ]_0^6\)
substituting limits into their integrated function and subtracting (in any order)
eg \(\pi (12(6)-(6)^{2})-\pi (0),72\pi -36\pi ,(12(6)-(6)^{2})-(0)\)
volume = \(36\pi \)
Question
a.Find \(\int {\frac{1}{{2x + 3}}} {\rm{d}}x\) .[2]
b.Given that \(\int_0^3 {\frac{1}{{2x + 3}}} {\rm{d}}x = \ln \sqrt P \) , find the value of P.[4]
▶️Answer/Explanation
Markscheme
\(\int {\frac{1}{{2x + 3}}} {\rm{d}}x = \frac{1}{2}\ln (2x + 3) + C\) (accept \(\frac{1}{2}\ln |(2x + 3)| + C\) ) A1A1 N2
[2 marks]
\(\int_0^3 {\frac{1}{{2x + 3}}} {\rm{d}}x = \left[ {\frac{1}{2}\ln (2x + 3)} \right]_0^3\)
evidence of substitution of limits (M1)
e.g.\(\frac{1}{2}\ln 9 – \frac{1}{2}\ln 3\)
evidence of correctly using \(\ln a – \ln b = \ln \frac{a}{b}\) (seen anywhere) (A1)
e.g. \(\frac{1}{2}\ln 3\)
evidence of correctly using \(a\ln b = \ln {b^a}\) (seen anywhere) (A1)
e.g. \(\ln \sqrt {\frac{9}{3}} \)
\(P = 3\) (accept \(\ln \sqrt 3 \) ) A1 N2
[4 marks]
Question
The graph of \(f(x) = \sqrt {16 – 4{x^2}} \) , for \( – 2 \le x \le 2\) , is shown below.
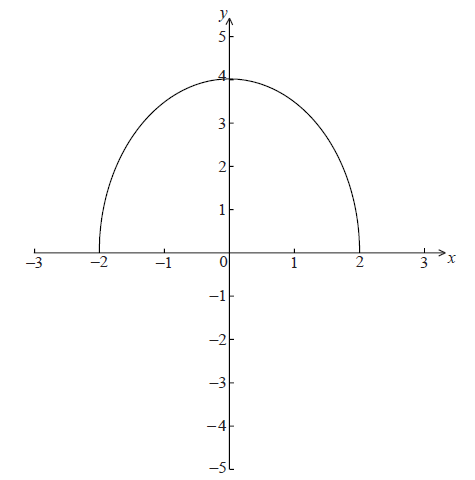
The region enclosed by the curve of f and the x-axis is rotated \(360^\circ \) about the x-axis.
Find the volume of the solid formed.
▶️Answer/Explanation
Markscheme
attempt to set up integral expression M1
e.g. \(\pi {\int {\sqrt {16 – 4{x^2}} } ^2}{\rm{d}}x\) , \(2\pi \int_0^2 {(16 – 4{x^2})} \) , \({\int {\sqrt {16 – 4{x^2}} } ^2}{\rm{d}}x\)
\(\int {16} {\rm{d}}x = 16x\) , \(\int {4{x^2}{\rm{d}}x = } \frac{{4{x^3}}}{3}\) (seen anywhere) A1A1
evidence of substituting limits into the integrand (M1)
e.g. \(\left( {32 – \frac{{32}}{3}} \right) – \left( { – 32 + \frac{{32}}{3}} \right)\) , \(64 – \frac{{64}}{3}\)
volume \(= \frac{{128\pi }}{3}\) A2 N3
[6 marks]
Question
Given that \(\int_0^5 {\frac{2}{{2x + 5}}} {\rm{d}}x = \ln k\) , find the value of k .
▶️Answer/Explanation
Markscheme
correct integration, \(2 \times \frac{1}{2}\ln (2x + 5)\) A1A1
Note: Award A1 for \(2 \times \frac{1}{2}( = 1)\) and A1 for \(\ln (2x + 5)\) .
evidence of substituting limits into integrated function and subtracting (M1)
e.g. \(\ln (2 \times 5 + 5) – \ln (2 \times 0 + 5)\)
correct substitution A1
e.g. \(\ln 15 – \ln 5\)
correct working (A1)
e.g. \(\ln \frac{{15}}{5},\ln 3\)
\(k = 3\) A1 N3
[6 marks]
Question
Let \(\int_\pi ^a {\cos 2x{\text{d}}x} = \frac{1}{2}{\text{, where }}\pi < a < 2\pi \). Find the value of \(a\).
▶️Answer/Explanation
Markscheme
correct integration (ignore absence of limits and “\(+C\)”) (A1)
eg \(\frac{{\sin (2x)}}{2},{\text{ }}\int_\pi ^a {\cos 2x = \left[ {\frac{1}{2}\sin (2x)} \right]_\pi ^a} \)
substituting limits into their integrated function and subtracting (in any order) (M1)
eg \(\frac{1}{2}\sin (2a) – \frac{1}{2}\sin (2\pi ),{\text{ }}\sin (2\pi ) – \sin (2a)\)
\(\sin (2\pi ) = 0\) (A1)
setting their result from an integrated function equal to \(\frac{1}{2}\) M1
eg \(\frac{1}{2}\sin 2a = \frac{1}{2},{\text{ }}\sin (2a) = 1\)
recognizing \({\sin ^{ – 1}}1 = \frac{\pi }{2}\) (A1)
eg \(2a = \frac{\pi }{2},{\text{ }}a = \frac{\pi }{4}\)
correct value (A1)
eg \(\frac{\pi }{2} + 2\pi ,{\text{ }}2a = \frac{{5\pi }}{2},{\text{ }}a = \frac{\pi }{4} + \pi \)
\(a = \frac{{5\pi }}{4}\) A1 N3
[7 marks]
