IB Mathematics AHL 5.17 Coupled differential equations AI HL Paper 2- Exam Style Questions- New Syllabus

(a)
The matrix is \( \begin{pmatrix} -4 & 0 \\ 3 & -2 \end{pmatrix} \).
Characteristic equation: \( \det\begin{pmatrix} -4 – \lambda & 0 \\ 3 & -2 – \lambda \end{pmatrix} = 0 \).
\( (-4 – \lambda)(-2 – \lambda) = 0 \).
So, \( \lambda = -4 \) or \( \lambda = -2 \).
For \( \lambda = -4 \): Solve \( \begin{pmatrix} 0 & 0 \\ 3x – 2y & 2 \end{pmatrix} \), giving \( 3x – 2y = 0 \), so \( x = \frac{2}{3}y \). Eigenvector is \( \begin{pmatrix} 2 \\ 3 \end{pmatrix} \) (or any multiple).
For \( \lambda = -2 \): Solve \( \begin{pmatrix} -2 & 0 \\ 3x – 2y & 0 \end{pmatrix} \), giving \( x = 0 \). Eigenvector is \( \begin{pmatrix} 0 \\ 1 \end{pmatrix} \) (or any multiple).
Explanation:
Eigenvalues are found from the characteristic equation; eigenvectors from the system with \( \lambda \) substituted.
Result:
Eigenvalues: \( \lambda = -4 \), \( \lambda = -2 \); Eigenvectors: \( \begin{pmatrix} 2 \\ 3 \end{pmatrix} \), \( \begin{pmatrix} 0 \\ 1 \end{pmatrix} \)

(b)
General solution: \( x = A e^{-4t} + B e^{-2t} \), \( y = \frac{3}{2} A e^{-4t} + C e^{-2t} \), where \( A, B, C \) are constants.
Explanation:
Use eigenvalues and eigenvectors to form the solution, adjusting for the system.
Result:
\( x = A e^{-4t} + B e^{-2t} \), \( y = \frac{3}{2} A e^{-4t} + C e^{-2t} \)

(c)
Both eigenvalues \( \lambda = -4 \) and \( \lambda = -2 \) are negative. Since \( e^{-4t} \to 0 \) and \( e^{-2t} \to 0 \) as \( t \to \infty \), the equilibrium point \( (0, 0) \) is stable.
Explanation:
Negative eigenvalues indicate a stable node where solutions decay to zero.
Result:
Stable

(d)
\( \frac{dy}{dx} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}} = \frac{3x – 2y}{-4x} \).
(i) At \( (4, 0) \): \( \frac{dy}{dx} = \frac{3 \times 4 – 2 \times 0}{-4 \times 4} = \frac{12}{-16} = -\frac{3}{4} \).
(ii) At \( (-4, 0) \): \( \frac{dy}{dx} = \frac{3 \times -4 – 2 \times 0}{-4 \times -4} = \frac{-12}{16} = -\frac{3}{4} \).
Explanation:
Use the ratio of differential equations to find the slope.
Result:
(i) \( -\frac{3}{4} \), (ii) \( -\frac{3}{4} \)

(e)
Phase portrait: .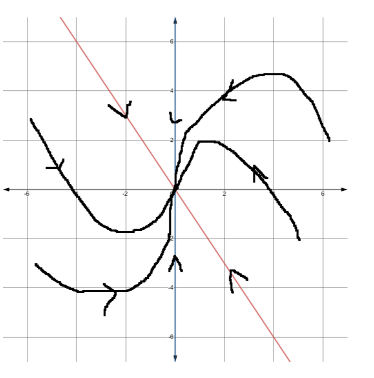
Shows trajectories converging to \( (0, 0) \) for \( -6 \leq x \leq 6 \), \( -6 \leq y \leq 6 \).
Explanation:
Sketch based on stable node behavior with negative eigenvalues.
Result:
Phase portrait as shown