IB MYP 4-5 Chemistry -Redox reactions- Study Notes - New Syllabus
IB MYP 4-5 Chemistry -Redox reactions- Study Notes
Key Concepts
- Redox Reactions (Oxidation and Reduction)
- Oxidation Numbers and Balancing Redox Equations
Redox Reactions (Oxidation and Reduction)
Redox Reactions (Oxidation and Reduction)
A redox reaction is a chemical reaction in which both oxidation and reduction occur simultaneously. One substance loses electrons (is oxidized), while another gains electrons (is reduced).
![]()
Oxidation and Reduction — Basic Definitions
| Process | Electron Definition | Oxygen Definition | Hydrogen Definition |
|---|---|---|---|
| Oxidation | Loss of electrons | Gain of oxygen | Loss of hydrogen |
| Reduction | Gain of electrons | Loss of oxygen | Gain of hydrogen |
Key Idea: Oxidation and reduction always occur together — when one substance loses electrons, another must gain them.
Oxidation and Reduction in Terms of Electrons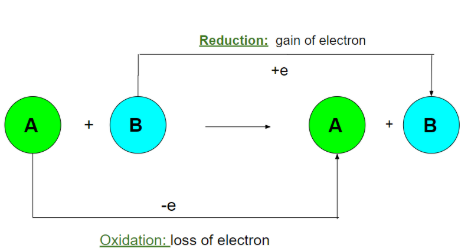
\( \mathrm{Oxidation: \ M \rightarrow M^{n+} + ne^-} \)
\( \mathrm{Reduction: \ X^{n+} + ne^- \rightarrow X} \)
For example:
\( \mathrm{Zn + Cu^{2+} \rightarrow Zn^{2+} + Cu} \)
- \( \mathrm{Zn} \) loses electrons → oxidized (reducing agent)
- \( \mathrm{Cu^{2+}} \) gains electrons → reduced (oxidizing agent)
Oxidizing and Reducing Agents
| Agent Type | Definition | Effect | Example |
|---|---|---|---|
| Oxidizing Agent | Substance that gains electrons and causes oxidation of another | Itself reduced | \( \mathrm{KMnO_4, \ Cl_2, \ HNO_3} \) |
| Reducing Agent | Substance that loses electrons and causes reduction of another | Itself oxidized | \( \mathrm{Zn, \ H_2, \ CO} \) |
Identifying Redox Reactions Using Oxidation Numbers
The oxidation number of an element shows how many electrons it has gained or lost in a compound. A change in oxidation number during a reaction indicates redox activity.
Rules:![]()
- Elements in their free state: oxidation number = 0
- Oxygen: −2 (except in peroxides, where −1)
- Hydrogen: +1 (except in metal hydrides, where −1)
- Sum of oxidation numbers in a compound = 0
- Sum of oxidation numbers in an ion = charge on the ion
Example: \( \mathrm{Zn + 2H^+ \rightarrow Zn^{2+} + H_2} \)
- \( \mathrm{Zn} \): 0 → +2 (oxidized)
- \( \mathrm{H} \): +1 → 0 (reduced)
- Hence, it is a redox reaction.
Common Redox Reactions in Daily Life
- Corrosion: Iron rusting (oxidation by oxygen and moisture)
- Combustion: Burning of fuels (oxidation releasing energy)
- Respiration: Biological oxidation of glucose to release energy
- Photosynthesis: Carbon dioxide reduced to glucose using sunlight
Example
Identify the oxidizing and reducing agents in the reaction \( \mathrm{Zn + 2HCl \rightarrow ZnCl_2 + H_2} \).
▶️ Answer / Explanation
Step 1: \( \mathrm{Zn} \) loses 2 electrons → oxidized (reducing agent).
Step 2: \( \mathrm{2H^+} \) gains 2 electrons → reduced (oxidizing agent).
Final Answer: Oxidizing agent = \( \mathrm{H^+} \); Reducing agent = \( \mathrm{Zn} \).
Example
Determine which element is oxidized and which is reduced in the reaction: \( \mathrm{2Fe^{3+} + Sn^{2+} \rightarrow 2Fe^{2+} + Sn^{4+}} \).
▶️ Answer / Explanation
Step 1: \( \mathrm{Fe^{3+}} \rightarrow \mathrm{Fe^{2+}} \) → gain of electrons → reduced.
Step 2: \( \mathrm{Sn^{2+}} \rightarrow \mathrm{Sn^{4+}} \) → loss of electrons → oxidized.
Final Answer: \( \mathrm{Fe^{3+}} \) is reduced; \( \mathrm{Sn^{2+}} \) is oxidized.
Example
Explain why the reaction \( \mathrm{Cl_2 + 2I^- \rightarrow 2Cl^- + I_2} \) is a redox reaction and identify the agents involved.
▶️ Answer / Explanation
Step 1: \( \mathrm{Cl_2 \rightarrow 2Cl^-} \): chlorine gains electrons → reduced (oxidizing agent).
Step 2: \( \mathrm{2I^- \rightarrow I_2} \): iodide loses electrons → oxidized (reducing agent).
Step 3: Both oxidation and reduction occur simultaneously.
Final Answer: Chlorine acts as oxidizing agent; iodide as reducing agent.
Oxidation Numbers and Balancing Redox Equations
Oxidation Numbers and Balancing Redox Equations
The oxidation number (also called oxidation state) of an element in a compound shows how many electrons an atom has lost, gained, or shared compared to its uncombined state.
Key Idea: Changes in oxidation numbers during a reaction indicate which substances are oxidized and which are reduced.
Rules for Assigning Oxidation Numbers
| Rule | Example |
|---|---|
| 1. The oxidation number of an element in its free state is 0. | \( \mathrm{O_2, H_2, N_2, Cl_2} \Rightarrow 0 \) |
| 2. The oxidation number of a simple ion equals its charge. | \( \mathrm{Na^+ = +1,\ Cl^- = -1} \) |
| 3. Oxygen is usually −2 (except in peroxides where −1). | \( \mathrm{H_2O: O = -2,\ H_2O_2: O = -1} \) |
| 4. Hydrogen is usually +1 (except in metal hydrides, −1). | \( \mathrm{HCl: H = +1,\ NaH: H = -1} \) |
| 5. The sum of oxidation numbers in a neutral compound is 0. | \( \mathrm{H_2O: 2(+1) + (-2) = 0} \) |
| 6. The sum of oxidation numbers in a polyatomic ion equals the ion’s charge. | \( \mathrm{SO_4^{2-}: S + 4(-2) = -2 \Rightarrow S = +6} \) |
Identifying Oxidation and Reduction by Oxidation Numbers
Oxidation: increase in oxidation number (loss of electrons)
![]()
Reduction: decrease in oxidation number (gain of electrons)
![]()
Example: \( \mathrm{Zn + Cu^{2+} \rightarrow Zn^{2+} + Cu} \)
- \( \mathrm{Zn: 0 \rightarrow +2} \) → oxidized (reducing agent)
- \( \mathrm{Cu: +2 \rightarrow 0} \) → reduced (oxidizing agent)
Balancing Redox Equations (Half-Reaction Method)
This method ensures that mass and charge are balanced. It involves separating the reaction into oxidation and reduction half-reactions.
Steps: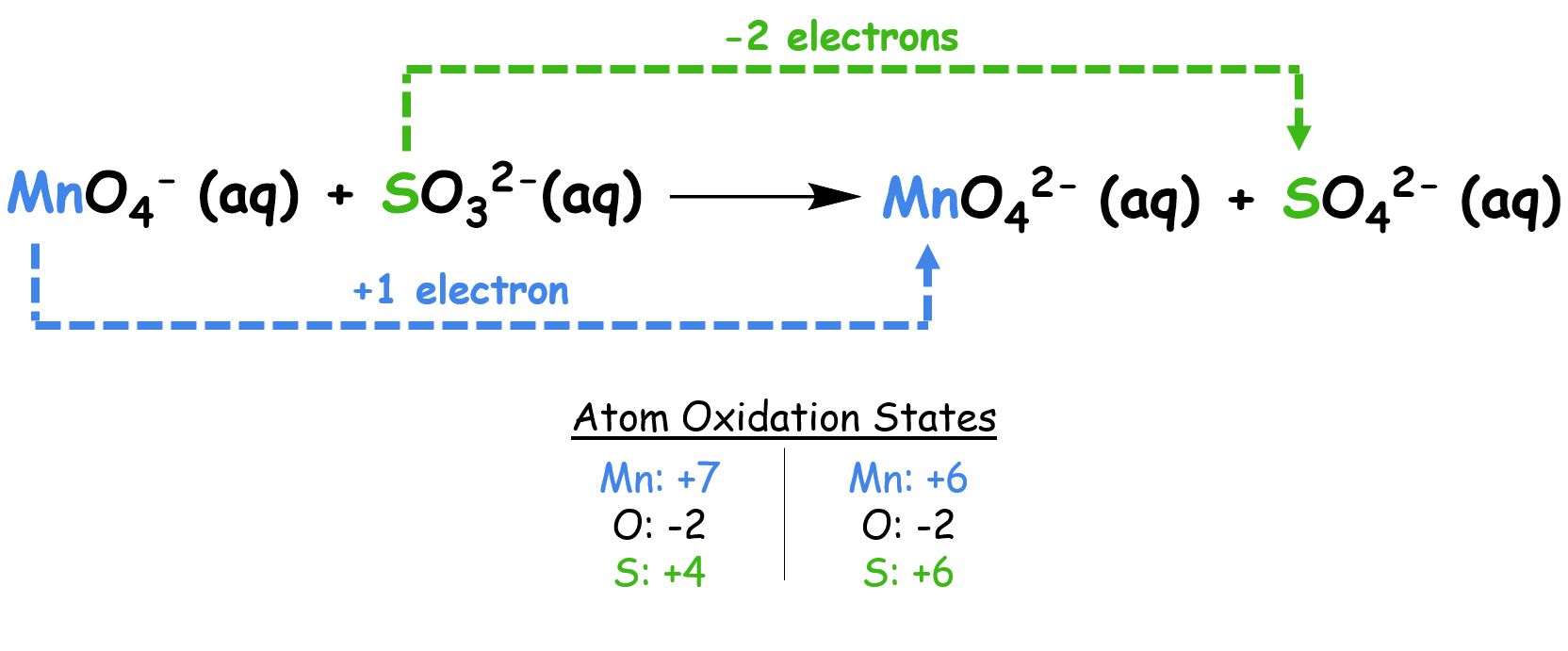
- Write the two half-reactions (oxidation and reduction separately).
- Balance all elements except hydrogen and oxygen.
- Balance oxygen using \( \mathrm{H_2O} \).
- Balance hydrogen using \( \mathrm{H^+} \).
- Balance charge by adding electrons \( \mathrm{(e^-)} \).
- Multiply half-equations so that electrons cancel.
- Add both half-reactions together.
Example of Half-Reaction Method
Reaction: \( \mathrm{Fe^{2+} + MnO_4^- \rightarrow Fe^{3+} + Mn^{2+}} \) (in acidic medium)
Step 1: Split into half-reactions
- Oxidation: \( \mathrm{Fe^{2+} \rightarrow Fe^{3+} + e^-} \)
- Reduction: \( \mathrm{MnO_4^- + 8H^+ + 5e^- \rightarrow Mn^{2+} + 4H_2O} \)
Step 2: Balance electrons
Multiply oxidation half by 5 so that both sides have 5 electrons.
Step 3: Combine both:
\( \mathrm{5Fe^{2+} + MnO_4^- + 8H^+ \rightarrow 5Fe^{3+} + Mn^{2+} + 4H_2O} \)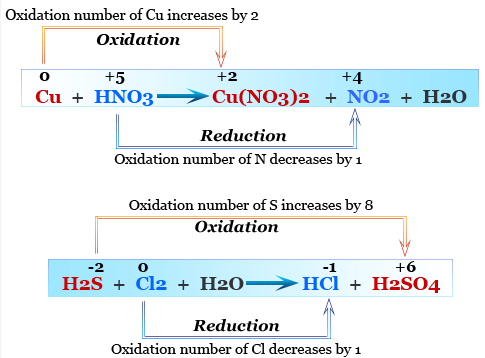
Final Answer: Balanced redox equation in acidic medium.
Oxidation Number Method (Alternative)
Used when balancing simple redox reactions without splitting into half-equations.
- Assign oxidation numbers to all elements.
- Identify which atoms are oxidized and reduced.
- Calculate total increase and decrease in oxidation numbers.
- Balance those changes by adjusting coefficients.
- Balance other atoms (O and H last).
Example
Assign oxidation numbers for all elements in \( \mathrm{H_2SO_4} \) and identify the oxidation number of sulfur.
▶️ Answer / Explanation
Let oxidation number of sulfur = x.
\( \mathrm{2(+1) + x + 4(-2) = 0} \)
→ \( \mathrm{x = +6} \)
Final Answer: Sulfur oxidation number = +6.
Example
Balance the redox reaction: \( \mathrm{Fe^{2+} + Cr_2O_7^{2-} \rightarrow Fe^{3+} + Cr^{3+}} \) in acidic medium.
▶️ Answer / Explanation
Step 1: Half-reactions:
- Oxidation: \( \mathrm{Fe^{2+} \rightarrow Fe^{3+} + e^-} \)
- Reduction: \( \mathrm{Cr_2O_7^{2-} + 14H^+ + 6e^- \rightarrow 2Cr^{3+} + 7H_2O} \)
Step 2: Multiply oxidation by 6:
\( \mathrm{6Fe^{2+} \rightarrow 6Fe^{3+} + 6e^-} \)
Step 3: Combine:
\( \mathrm{6Fe^{2+} + Cr_2O_7^{2-} + 14H^+ \rightarrow 6Fe^{3+} + 2Cr^{3+} + 7H_2O} \)
Final Answer: Balanced redox equation in acidic solution.
Example
Balance the redox reaction \( \mathrm{MnO_4^- + C_2O_4^{2-} \rightarrow Mn^{2+} + CO_2} \) in acidic medium.
▶️ Answer / Explanation
Step 1: Half-reactions:
- Oxidation: \( \mathrm{C_2O_4^{2-} \rightarrow 2CO_2 + 2e^-} \)
- Reduction: \( \mathrm{MnO_4^- + 8H^+ + 5e^- \rightarrow Mn^{2+} + 4H_2O} \)
Step 2: Multiply oxidation half by 5 and reduction half by 2.
Step 3: Combine:
\( \mathrm{2MnO_4^- + 5C_2O_4^{2-} + 16H^+ \rightarrow 2Mn^{2+} + 10CO_2 + 8H_2O} \)
Final Answer: Balanced redox reaction in acidic conditions.
