Question
Let X be normally distributed with mean 100 cm and standard deviation 5 cm.
a.On the diagram below, shade the region representing \({\rm{P}}(X > 105)\) .[2]
b.Given that \({\rm{P}}(X < d) = {\rm{P}}(X > 105)\) , find the value of \(d\) . [2]
c.Given that \({\rm{P}}(X > 105) = 0.16\) (correct to two significant figures), find \({\rm{P}}(d < X < 105)\) . [2]
▶️Answer/Explanation
Markscheme
a.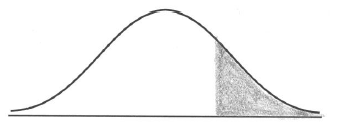 A1A1 N2
A1A1 N2
Note: Award A1 for vertical line to right of mean, A1 for shading to right of their vertical line.
evidence of recognizing symmetry (M1)
e.g. \(105\) is one standard deviation above the mean so \(d\) is one standard deviation below the mean, shading the corresponding part, \(105 – 100 = 100 – d\)
\(d = 95\) A1 N2
[2 marks]
evidence of using complement (M1)
e.g. \(1 – 0.32\) , \(1 – p\)
\({\rm{P}}(d < X < 105) = 0.68\) A1 N2
[2 marks]
Question
The random variable X is normally distributed with mean 1000 and standard deviation 50.
(a) Find (i) \(P(X < 925)\) (ii) \(P(925 < X < 1025)\) (iii) \(P(X > 1025)\)
(b) Sketch a graph representing the information in \((a)\)
(c) Find the standardised values of \(925\) and \(1025\)
(d) Sketch the corresponding graph of standardised values
(e) Find \(E(X^{2})\)
▶️Answer/Explanation
Ans
(a) (i) \(P(X<925)=0.0668\) (ii) \(P(925<X<1025)\) (iii) \(P(X>1025)=0.309\)
(b) 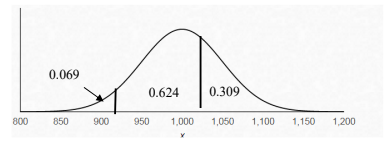
(c) \(-1.5\) and \(0.5\) respectively
(d) similar to the above the vertical boundaries are \(-1.5\) and \(0.5\)
(e) \(E(X^{2})=Var(X)+E(X)^{2}=\sigma ^{2}+\mu ^{2}=50^{2}+1000^{2}=1002500\)
Question
The random variable \(X\) is normally distributed with mean \(1000\) and standard deviation \(50\).
(a) 30% is more than \(a\). Find \(a\)
(b) 57% is less than \(b\). Find \(b\)
(c) 60% is between \(c\) and \(d\), where \(c\) and \(d\) are symmetric about the mean. Find \(c\) and \(d\)
(d) Find the interquartile range.
▶️Answer/Explanation
Ans
\(a =1026\) \(b=1008.8\) \(c=958\) and \(d=1042\) IQR=\(1033.7-966.3=67.4\)
Question
The random variable \(X\) is normally distributed. 17% is less than \(100\) while 57% is less than \(200\). Find the mean and the standard deviation.
▶️Answer/Explanation
Ans
\(Z_{1}=\frac{X-\mu }{\sigma }\Rightarrow \frac{100-\mu }{\sigma}=-0.9542\Rightarrow \mu -0.9542\sigma =100\)
\(Z_{2}=\frac{X-\mu }{\sigma }\Rightarrow \frac{200-\mu }{\sigma}=-0.1764\Rightarrow \mu +0.1764\sigma =200\)
\(\mu =184.4 \sigma =88.45\)
Question
The weight of the population of a particular animal is normally distributed with mean \(300kg\) and standard deviation\(40kg\). Animals above \(350kg\) are considered overweight.
(a) Find the probability that an animal is overweight given that it is more than \(300kg\).
(b) We select \(1000\) animals. Find the expected number of the overweight animals.
(c) We select two animals. Find the probability that
(i) both animals are overweight.
(ii) only one of the animals is overweight.
(iii) at least one of the animals is overweight.
(d) We select eight animals. Find the probability that
(i) half of the animals are overweight.
(ii) at least one of the animals is overweight.
▶️Answer/Explanation
Ans
(a) \(P(X>350|X>300)=\frac{P(X>350)}{P(X>300)}=\frac{0.1056}{0.50}=0.211\)
(b) \(1000\times 0.1056=106\)
(c) We select two animals. Find the probability that
(i) \((0.1056)^{2}=0.0112\)
(ii) \(0.1056\times (1-0.1056)\times 2=0.189\)
(iii) \(0.0112+0.189=0.2\)
(d) Binomial with \(n=8\) and \(p=0.1056\) (i) \(0.00563\) (ii) \(1-0.408=0.592\)
Question
The following diagram shows the probability density function for the random variable \(X\), which is normally distributed with mean \(250\) and standard deviation \(50\).
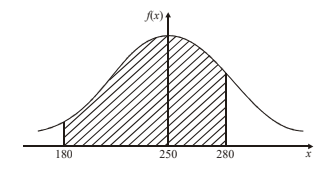
Find the probability represented by the shaded region.
▶️Answer/Explanation
Ans
\(P(180<X<280)=0.645\)
Question
The random variable \(X\) is distributed normally with mean \(30\) and standard deviation \(2\). Find \(p(27\leq X\leq 34)\).
▶️Answer/Explanation
Ans
\(p(27\leq X\leq 34)=0.910(3\ s.f.)(accept\ 0.911)\)
Question
The diameters of discs produced by a machine are normally distributed with a mean of \(10\) cm and standard deviation of \(0.1\) cm. Find the probability of the machine producing a disc with a diameter smaller than \(9.8\) cm.
▶️Answer/Explanation
Ans
Let \(X\) be the random variable “the diameter of the disc,”then \(X\sim N(10,0.1^{2})\).
Using a graphic display calculator, \(P(X<9.8)=0.0228\)
Question
The diameters of discs produced by a machine are normally distributed with a mean of \(10\) cm and standard deviation of \(0.1\) cm. Find the probability of the machine producing a disc with a diameter smaller than \(9.8\) cm.
▶️Answer/Explanation
Ans
Let \(X\) be the random variable “the diameter of the disc,”then \(X\sim N(10,0.1^{2})\).
Using a graphic display calculator, \(P(X<9.8)=0.0228\)
Question
Let \(X\) be a normal random variable with mean \(25\) and variance 4. Find \(P(\left | X-25 \right |<3)\).
▶️Answer/Explanation
Ans
\(P(\left | X-25 \right |<3)=P(22<X<28)\)
standard deviation=\(2\) (need not be seen)
\(P(\left | X-25 \right |<3)=0.866\)
Question
The lengths of a particular species of lizard are normally distributed with a mean length of \(50\) cm and a standard deviation of \(4\) cm. A lizard is chosen at random.
(a) Find the probability that its length is greater than \(45\) cm.
(b) Given that its length is greater than \(45\) cm, find the probability that its length is greater than \(55\) cm.
▶️Answer/Explanation
Ans
(a) \(P(X>45)=P(Z<1.25)\)
=0.894\)
(b) Using conditional probability \(P(X>55|X>45)\)
\(=\frac{P(X>55\cap X>45)}{P(X>45)}\)
\(=\frac{P(X>55)}{P(X>45)}\left ( =\frac{0.1056…}{0.8943…} \right )\)
FT numerator = 1-(their answer to a).
\(=0.118\)
Question
\(Z\) is the standardised normal random variable with mean \(0\) and variance \(1\). Find the value of a such that \(P\left (\left | Z \right |\leq a \right ) =0.75\).
▶️Answer/Explanation
Ans
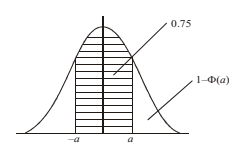
From the diagram using inverse normal \(a = 1.15\)
Question
A certain type of vegetable has a weight which follows a normal distribution with mean \(450\) grams and a standard deviation \(50\) grams.
(a) In a load of \(2000\) of these vegetables, calculate the expected number with a weight greater than \(525\) grams.
(b) Find the upper quartile of the distribution.
▶️Answer/Explanation
Ans
(a) P(weight >\(525\) grams) = \(0.0668\)
Expected number \(\geq 525\) grams=(\(2000\))(\(0.0668\))=\(134\)
(b) Inversed Normal: \(P(X<Q_{3})=0.75\) OR \(P(X>Q_{3})=0.25\)
\(Q_{3}=484\)
Question
A factory has a machine designed to produce \(1\) kg bags of sugar. It is found that the average weight of sugar in the bags is \(1.02\) kg. Assuming that the weights of the bags are normally distributed, find the standard deviation if \(1.7\)% of the bags weigh below \(1\) kg. Give your answer correct to the nearest \(0.1\) gram.
▶️Answer/Explanation
Ans
\(P(Z<z)=0.017\) \(z=-2.12\)
But \(z=\frac{x-\mu }{\sigma }=\frac{1-1.02}{\sigma }\) where \(x=1\)kg
Therefore \(\frac{1-1.02}{\sigma }=-2.12\Leftrightarrow \sigma =0.00943\) kg=\(9.4g\)
Question
The weights in grams of bread loaves sold at a supermarket are normally distributed with mean \(200\) g. The weights of 88% of the loaves are less than \(220\)g. Find the standard deviation.
▶️Answer/Explanation
Ans
For writing \(P(W<220)=0.88\) or sketching an appropriate diagram
\(z=1.17(499…) (accept 1.17 or 1.18)\)
Using \(z=\frac{x-\mu }{\sigma }\)
\(z=\frac{220-200}{\sigma }\)
\(\Rightarrow \sigma =17.0\) (grams) (accept \(16.9\) or \(17.1\))
Question
The speeds of cars at a certain point on a straight road are normally distributed with mean \(μ\) and standard deviation σ. 15 % of the cars travelled at speeds greater than \(90\ km\ h^{-1}\) and \(12\) % of them at speeds less than \(40\ km\) \(h^{-1}\). Find μ and σ.
▶️Answer/Explanation
Ans
\(P(X>90)=0.15 and P(X<40)=0.12\)
\(1.036=\frac{90-\mu }{\sigma }, -1.175=\frac{40-\mu }{\sigma }\)
\(\mu =66.6, \sigma =22.6\)
Question
The random variable X is normally distributed and \(P(X\leq 10)=0.670\), \(P(X\leq 12)=0.0937\).
Find E(X).
▶️Answer/Explanation
Ans
Let \(E(X)=\mu, z_{1}=0.44, z_{2}=1.53\)
\(10=\mu +0.44\sigma\)
\(12=\mu +1.53\sigma\)
\(\mu =\frac{1.53\times 10-0.44\times 12}{1.53-0.44}=>E(X)=9.19\)
Question
A furniture manufacturer makes tables. A table leg is considered to be oversize if its width is greater than \(10.5\) cm and undersize of its width is less than \(9.5\) cm. From past experience it is found that \(2\)% of the table legs that are made are oversize and that \(4\)% of the table legs are undersize. The widths of the table legs are normally distributed with mean \(μ\) cm and standard deviation \(σ\) cm. Find the value of and \(μ\) of \(σ\).
▶️Answer/Explanation
Ans
\(P(X>10.5)=0.02\)
\(\Rightarrow \frac{10.5-\mu }{\sigma }=2.05…\)
\(P(X<9.5)=0.04\)
\(\Rightarrow \frac{9.5-\mu }{\sigma }=-1.75…\)
\(10.5-\mu =2.054\sigma\)
\(9.5-\mu =-1.751\sigma\)
\(\Rightarrow 1=3.805\sigma\)
\(\Rightarrow \sigma =0.263\)
\(\Rightarrow \mu =9.96\)
Question
A random variable \(X\) is normally distributed with mean \(μ\) and standard deviation \(σ\), such that \(P(X> 50.32)=0.119\), and \(P(X< 43.56)=0.305\)
(a) Find \(μ\) and \(\sigma \).
(b) Hence find \(P(\left | X-\mu \right |< 5)\).
▶️Answer/Explanation
Ans
(a) 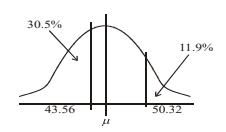
\(z_{1}=1.18 z_{2}=-0.51\)
\(\frac{50.32-\mu }{\sigma }=1.18 and \frac{43.56-\mu }{\sigma }=-0.51\)
Solving simultaneously
\(\Rightarrow 50.32=\mu +1.18\sigma and 43.56=\mu -0.51\sigma\)
\(\Rightarrow 1.69\sigma =6.76\Rightarrow \sigma =4\Rightarrow \mu =45.6\)
(b) \(P(\left | X-\mu \right |<5)=P(40.6<x<50.6)=0.789\)
MAA SL 4.11 NORMAL DISTRIBUTION [concise]-neha
Question
[with GDC]
The random variable \(X\) is normally distributed with \(μ = 100\) and \(σ = 20\), i.e. \(N(100,20^{2})\).
(a) Find the probabilities
(i) \(P(X < 90)\) (ii) \(P(90 < X < 130)\) (iii) \(P(X > 130)\)
(b) Sketch a diagram to represent the information in question (a).
(c) Write down the standardised values of \(90, 100\) and \(130\).
(d) Sketch a diagram, similar that of (b), containing the standardised values above.
▶️Answer/Explanation
Ans
(a) \(P(X < 90) = 0.308\) \(P(90 < X < 130) = 0.625\) \(P(X > 130) = 0.067\)
(b) 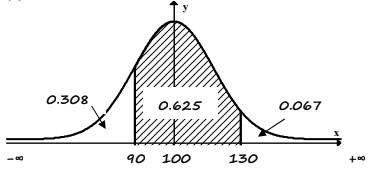
(c) The standardised values are \(-0.5, 0\) and \(1.5\) respectively
(d) 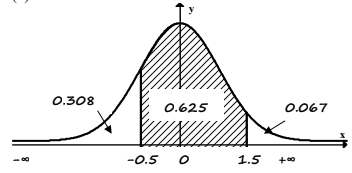
Question
[with GDC]
The random variable \(X\) follows a normal distribution with \(μ = 100\) and \(σ = 20\).
(a) Given that \(P(X < a) = 0.8\) find the value of \(a\).
(b) Given that \(P(X > b) = 0.3\) find the value of \(b\).
(c) Find \(Q_{1}\) and \(Q_{3}\).
▶️Answer/Explanation
Ans
(a) (use tail left, area \(0.8\)) a = \(116.8\)
(b) (use tail right, area \(0.3\)) b=\(110.5\)
(c) (use tail central, area \(0.5\)) \(Q_{1}=86.5\) and \(Q_{3}=113.5\)
Question
[without GDC]
The random variable \(X\) is normally distributed with \(μ = 100\). It given that \(P(X > 130) = 0.2\)
Write down the values of the following probabilities
(a) \(P(X < 130)\)
(b) \(P(X < 70)\)
(c) \(P(100<X < 130)\)
(d) \(P(70<X < 130)\)
▶️Answer/Explanation
Ans
(a) \(P(X < 130)\) = \(0.8\)
(b) \(P(X < 70) = 0.2\)
(c) \(P(100<X < 130) = 0.3\)
(d) \(P(70<X < 130) = 0.6\)
Question
[with GDC]
The random variable \(X\) follows a normal distribution with mean \(μ\) unknown and \(σ = 20\).
Given that \(P(X < 130) = 0.8\) find the value of \(μ\).
▶️Answer/Explanation
Ans
\(\frac{X-\mu }{\sigma }=z\Leftrightarrow \frac{130-\mu }{20}=0.842\)
\(\Leftrightarrow \mu =113.2\)
Question
[with GDC]
For the normally distributed random variable \(X, P(X < 60) = 0.2\) and \(P(X > 130) = 0.1\).
Find the values of \(μ\) and of \(σ\).
▶️Answer/Explanation
Ans
We use \(\frac{X-\mu }{\sigma }\)= \(z\) twice.
\(\frac{60-\mu }{\sigma }=-0.84162\Leftrightarrow 60-\mu =-0.84162\sigma \Leftrightarrow \mu -0.84162\sigma =60\)
\(\frac{130-\mu }{\sigma }=1.28155 \Leftrightarrow 130-\mu =1.28155\sigma \Leftrightarrow \mu +1.28155\sigma =130\)
System gives \(\mu =87.7\) and \(\sigma =33.0\)
Question
[with GDC]
The weight \(X\) of a particular animal is normally distributed with \(μ = 200\) kg and \(σ = 15\)kg.
An animal of this population is overweight if it has weight greater than \(230\) kg
(a) Find the probability than an animal is overweight.
(b) We select \(2\) animals of this population. Find the probabilities that
(i) both animals are overweight (ii) only one animal is overweight.
(c) We select \(7\) animals of this population. Find the probability that exactly two of them are overweight.
▶️Answer/Explanation
Ans
(a) \(P(X > 230)= 0.02275\)
(b) (i) \((0.02275)^{2}=0.000518\) (ii) \((0.02275)\times (1-0.02275)\times 2=0.0445\)
(c) \(Y\) follows \(B (n , p )\) with \(n = 7, p = 0.02275\)
\(P (Y= 2) 0.00969\)
Question
[with GDC]
The mass of packets of a breakfast cereal is normally distributed with a mean of \(750\) g and standard deviation of \(25\) g.
(a) Find the probability that a packet chosen at random has mass
(i) less than \(740\) g; (ii) at least \(780\) g; (iii) between \(740\) g and 780\) g.
(b) Two packets are chosen at random. What is the probability that both packets have a mass which is less than \(740\) g?
(c) The mass of \(70\)% of the packets is more than \(x\) grams. Find the value of \(x\).
▶️Answer/Explanation
Ans
(a) \(M\sim N(750,625)\)
(i) \(P (M < 740 g) = 0.345\)
(ii) \(P (M > 780 g) = 0.115\)
(iii) \(P(740 < M < 780) = 0.540\)
(b) P (both < \(740\)) = \(0.345^{2}=0.119\)
(c) x = \(737\) g
Question
[with GDC]
The heights, \(H\), of the people in a certain town are normally distributed with mean \(170\) cm and standard deviation \(20\) cm.
(a) A person is selected at random. Find the probability that his height is less than \(185\) cm.
(b) Given that \(P(H >d) = 0.6808\), find the value of \(d\).
▶️Answer/Explanation
Ans
(a) \(0.773\)
(b) \(d = 161\)
Question
[with GDC]
The heights of a group of students are normally distributed with a mean of \(160\) cm and a standard deviation of 20 cm.
(a) A student is chosen at random. Find the probability that the student’s height is greater than \(180\) cm.
(b) In this group of students, \(11.9\)% have heights less than \(d\) cm. Find the value of \(d\).
▶️Answer/Explanation
Ans
(a) \(0.159\)
(b) \(d = 136\)
Question
[with GDC]
The weights of a group of children are normally distributed with a mean of \(22.5\) kg and a standard deviation of \(2.2\) kg.
(a) Write down the probability that a child selected at random has a weight more than \(25.8\) kg.
(b) Of the group \(95\)% weigh less than \(k\) kilograms. Find the value of \(k\).
(c) The diagram below shows a normal curve. On the diagram, shade the region that represents the following information:
▶️Answer/Explanation
Ans
(a) \(0.0668\)
(b) \(k = 26.1\) kg
(c) 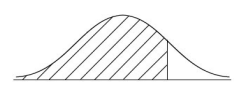
Question
[with GDC]
Intelligence Quotient (IQ) in a certain population is normally distributed with a mean of \(100\) and a standard deviation of \(15\).
(a) What percentage of the population has an IQ between \(90\) and \(125\)?
(b) If two persons are chosen at random from the population, what is the probability that both have an IQ greater than \(125\)?
▶️Answer/Explanation
Ans
(a) P\((90 < X < 125) = 0.701\)
\(70.1\) percent of the population (accept \(70\) percent).
(b) \(P(X\geq 125)=0.0478\)
P(both persons having \(IQ\geq 125) = (0.0478)^{2}=0.00228\)
Question
[with GDC]
The heights of certain plants are normally distributed. The plants are classified into three categories.
The shortest \(12.92\)% are in category A.
The tallest \(10.38\)% are in category C.
All the other plants are in category B with heights between \(r\) cm and \(t\) cm.
(a) Complete the following diagram to represent this information.
(b) Given that the mean height is \(6.84\) cm and the standard deviation \(0.25\) cm, find the value of \(r\) and of \(t\).
▶️Answer/Explanation
Ans
(a) 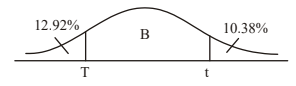
(b) \(r = 6.56\) \(t = 7.16\)
Question
[with GDC]
It is claimed that the masses of a population of lions are normally distributed with a mean mass of \(310\) kg and a standard deviation of \(30\) kg.
(a) Calculate the probability that a lion selected at random will have a mass of \(350\) kg or more.
(b) The probability that the mass of a lion lies between \(a\) and \(b\) is \(0.95\), where \(a\) and \(b\) are symmetric about the mean. Find the value of \(a\) and of \(b\).
▶️Answer/Explanation
Ans
(a) \(P(M \geq 350) = 0.0912\)
(b) 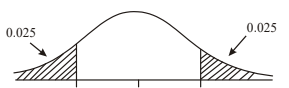
either tail left, tail right for each endpoint or directly tail central with Area = \(0.95\)
\(251 < M < 369\)
Question
[with GDC]
Residents of a small town have savings which are normally distributed with a mean of \($ 3000\) and a standard deviation of \($500\).
(a) What percentage of townspeople have savings greater than \($ 3200\)?
(b) Two townspeople are chosen at random. What is the probability that both of them have savings between \($ 2300\) and \($ 3300\)?
(c) The percentage of townspeople with savings less than d dollars is \(74.22\)%. Find \(d\).
▶️Answer/Explanation
Ans
(a) \(0.345\) (\(34.5\)%)
(b) \(P(2 300 < X < 3 300) =0.645\)
P(both)= (0.645)^{2}=0.416
(c) d = \($ 3 325\) ( \($ 3 330\) to \(3\) s.f.) (Accept $\(3325.07\))
Question
[with GDC]
A company manufactures television sets. They claim that the lifetime of a set is normally distributed with a mean of 80 months and standard deviation of 8 months.
(a) What proportion of television sets break down in less than \(72\) months?
(b) (i) Calculate the proportion of sets with a lifetime between \(72\) and \(90\) months.
(ii) Illustrate this proportion by a sketch of a normal distribution curve.
(c) If a set breaks down in less than \(x\) months, the company replace it free of charge.
They replace \(4\)% of the sets. Find the value of \(x\).
▶️Answer/Explanation
Ans
\(X\sim N (80,8^{2})\)
(a) \(P(X < 72) = 0.159\)
(b) (i) \(P(72 < X < 90) = 0.736\)
(ii) 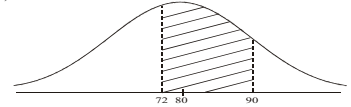
(c) \(x\) =\( 66.0\) months
Question
[without GDC]
A random variable \(X\) is distributed normally with a mean of \(100\) and a variance of \(100\).
(a) Find the value of \(X\) that is \(1.12\) standard deviations above the mean.
(b) Find the value of \(X\) that is \(1.12\) standard deviations below the mean.
▶️Answer/Explanation
Ans
\(\sigma =10, 1.12\times 10=11.2\)
(a) \(100 + 11.2 = 111.2\)
(b) \(100 – 11.2 = 88.8\)
Question
[without GDC]
The heights of trees in a forest are normally distributed with mean height \(17\) metres. One tree is selected at random. The probability that a selected tree has a height greater than \(24\) metres is \(0.06\).
(a) Find the probability that the tree selected has a height less than \(24\) metres.
(b) The probability that the tree has a height less than \(D\) metres is \(0.06\). Find \(D\).
(c) A woodcutter randomly selects \(200\) trees. Find the expected number of trees whose height lies between \(17\) metres and \(24\) metres.
▶️Answer/Explanation
Ans
(a) \(p = 0.94\)
(b) \(D = 10\)
(c) \(P(17 < H < 24) = 0.44\)
\(E(trees) = 200 × 0.44= 88\)
Question
[with GDC]
In a country called Tallopia, the height of adults is normally distributed with a mean of \(187.5\) cm and a standard deviation of \(9.5\) cm.
(a) What percentage of adults in Tallopia have a height greater than \(197\) cm?
(b) A standard doorway in Tallopia is designed so that \(99\)% of adults have a space of at least \(17\) cm over their heads when going through a doorway. Find the height of a standard doorway in Tallopia. Give your answer to the nearest cm.
▶️Answer/Explanation
Ans
(a) \(P (H > 197) = 0.159 = 15.9\)%
(b) \(99\)% of heights under \(209.6 = 210\) cm (\(3\) sf)
Height of standard doorway = \(210 + 17 = 227\) cm
Question
[with GDC]
The heights of boys at a particular school follow a normal distribution with a standard deviation of \(5\) cm. The probability of a boy being shorter than \(153\) cm is \(0.705\).
(a) Calculate the mean height of the boys.
(b) Find the probability of a boy being taller than \(156\) cm.
▶️Answer/Explanation
Ans
(a) \(P(H < 153) = 0.705\)
Standardizing \(\frac{153-\mu }{5}=0.5388…\)
\(\mu =150.30…= 150\) (to \(3\)sf)
(b) \(0.128\)
Question
[with GDC]
The scores of a test given to students are normally distributed with a mean of \(21.80\)% of the students have scores less than \(23.7\).
(a) Find the standard deviation of the scores.
A student is chosen at random. This student has the same probability of having a score less than \(25.4\) as having a score greater than \(b\).
(b) (i) Find the probability the student has a score less than \(25.4\).
(ii) Find the value of \(b\).
▶️Answer/Explanation
Ans
(a) \(0.84…=\frac{23.7-21}{\sigma }\Rightarrow \sigma =3.21\)
(b) (i) \(P(X < 25.4) = 0.915\)
(ii) \(b=21-4.4\Rightarrow b=16.6\)
Question
[with GDC]
The heights of certain flowers follow a normal distribution. It is known that \(20\)% of these flowers have a height less than \(3\)cm and \(10\)% have a height greater than \(8\) cm.
Find the value of the mean \(μ\) and the standard deviation \(σ\).
▶️Answer/Explanation
Ans
\(X\sim N(\mu ,\sigma ^{2})\),
\(\frac{3-\mu }{\sigma }=0.8416, \frac{8-\mu }{\sigma }=1.282\)
\(3-\mu =-0.8416\sigma\)
\(8-\mu =1.282\sigma\)
\(\sigma =2.35, \mu =4.99\)
Question
[with GDC]
The heights of certain flowers follow a normal distribution. It is known that \(20\)% of these flowers have a height less than \(3\)cm and \(10\)% have a height greater than \(8\) cm.
Find the value of the mean \(μ\) and the standard deviation \(σ\).
▶️Answer/Explanation
Ans
\(X\sim N(\mu ,\sigma ^{2})\),
\(\frac{3-\mu }{\sigma }=0.8416, \frac{8-\mu }{\sigma }=1.282\)
\(3-\mu =-0.8416\sigma\)
\(8-\mu =1.282\sigma\)
\(\sigma =2.35, \mu =4.99\)
Question
[with GDC]
The speeds of cars at a certain point on a straight road are normally distributed with mean \(μ\) and standard deviation \(σ\). \(15\) % of the cars travelled at speeds greater than \(90 \ km \ h^{-1}\) and \(12\) % of them at speeds less than \(40\ km\ h^{-1}\). Find \(μ\) and \(σ\).
▶️Answer/Explanation
Ans
\(P(X > 90) = 0.15\) and \(P(X < 40) = 0.12\)
\(1.036=\frac{90-\mu }{\sigma},-1.175=\frac{40-\mu }{\sigma }\)
\(\mu =66.6, \sigma =22.6\)
Question
[with GDC]
A box contains a large number of biscuits. The weights of biscuits are normally distributed with mean \(7\) g and standard deviation \(0.5\) g.
(a) One biscuit is chosen at random from the box. Find the probability that this biscuit
(i) weighs less than \(8\) g; (ii) weighs between \(6\) g and \(8\) g.
(b) Five percent of the biscuits in the box weigh less than \(d\) grams.
(i) Complete the following normal distribution diagram, to represent this information, by indicating \(d\), and shading the appropriate region.
(ii) Find the value of \(d\).
(c) The weights of biscuits in another box are normally distributed with mean \(μ\) and standard deviation \(0.5\) g. It is known that \(20\)% of the biscuits in this second box weigh less than \(5\) g. Find the value of \(μ\).
▶️Answer/Explanation
Ans
\(X\sim N (7,0.5^{2})\)
(a) (i) \(P(X < 8) = 0.977\) (ii) \(P(6 < X < 8) = 0.95\)
(b) (i) 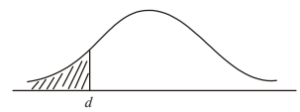
(ii) \(d = 6.18\)
(c) \(Y\sim N(\mu ,0.5^{2}), P(Y<5)=0.2\)
\(\frac{5-\mu }{0.5}=-0.8416 \mu =5.42\)
Question
[with GDC]
The lifespan of a particular species of insect is normally distributed with a mean of \(57\) hours and a standard deviation of \(4.4\) hours.
(a) The probability that the lifespan of an insect of this species lies between \(55\) and \(60\) hours is represented by the shaded area in the following diagram. This diagram represents the standard normal curve.
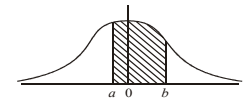
(i) Write down the values of \(a\) and \(b\).
(ii) Find the probability that the lifespan of an insect of this species is
(a) more than \(55\) hours; (b) between \(55\) and \(60\) hours.
(b) \(90\)% of the insects die after \(t\) hours.
(i) Represent this information on a standard normal curve diagram, similar to the one given in part (a), indicating clearly the area representing \(90\)%.
(ii) Find the value of \(t\).
▶️Answer/Explanation
Ans
(a) Let \(X\) be the lifespan in hours, \(X\sim N(57, 4.4^{2})\)
(i) \(a = –0.455\) (\(3\) sf) b = \(0.682\) (\(3\) sf)
(ii) (a) P \((X > 55)\) = \(0.675\) (b) \(P(55\leq X\leq 60)=0.428\) (\(3\) sf)
(b) \(90\)% have died \(\Rightarrow\) shaded area = \(0.9\)
\(t = 62.6\) hours
