Question 1 [Maximum mark: 4]
George goes fishing. From experience he knows that the mean number of fish he catches per hour is 1.1. It is assumed that the number of fish he catches can be modelled by a Poisson distribution.
On a day in which George spends 8 hours fishing, find the probability that he will catch more than 9 fish.
▶️Answer/Explanation
X ~ Po (8.8) Note: Award (M1) for calculating the mean, 8.8, of the distribution P (X >9) = P(X ≥ 10) OR P (X >9) = 1 – P ( X ≤ 9) P (X >9) = 0.386 (0.386260…) Note: Award (M1)(M0)(M1)A0 for finding P (X ≤9) = 0.518 (0.517719…) OR P (X ≤9) = 0.614 (0.613740…)
[MAI 4.12] POISSON DISTRIBUTION-loyola
Question
[Maximum mark: 12]
The random variable X has a Poisson distribution with mean 2.5.
(a) Calculate the following probabilities.
| P(X = 3) | P(3 ≤ X ≤ 5) | ||
| P(X ≤ 3) | P(X ≥ 3) | ||
| P(X < 3) | P(X > 3) |
(b) Calculate the following conditional probabilities
| P(X = 3| X ≥ 3) | |
| P(X ≤ 5| X ≥ 3) | |
| P(X≥ 5| X ≥ 3) | |
| P(X≤ 3| X ≤ 5) |
c) Find the mode of X.
▶️Answer/Explanation
Answer:
(a) 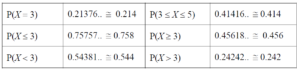
(b) 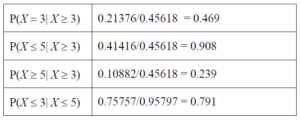
(c) P(X = 2) = 0.257 and P(X = 3) = 0.214, hence mode = 2
Question
[Maximum mark: 10]
The average number of phone calls in a phone centre is 2 phone calls per minute.
Find
(a) The probability of 1 phone call in one minute. [2]
(b) The probability of 2 phone calls in one minute. [2]
(c) The probability of 1 phone call in two minutes. [2]
(d) The probability of 2 phone calls in two minutes. [2]
(e) The probability of no phone calls in half a minute. [2]
▶️Answer/Explanation
Answer:
(a) For m = 2 P(X = 1) = 0.271
(b) For m = 2 P(X = 2) = 0.271
(c) For m = 4 P(X = 1) = 0.0733
(d) For m = 4 P(X = 2) = 0.147
(e) For m = 1 P(X = 0) = 0.368
Question
[Maximum mark: 8]
The average number of phone calls in a phone centre is 1 phone call per two minutes.
Find
(a) The probability of 1 phone call in two minutes. [2]
(b) The probability of 1 phone call in one minute. [2]
(c) The probability of no phone calls in one minute. [2]
(d) The probability of 3 phone calls in four minutes. [2]
▶️Answer/Explanation
Answer:
(a) For m = 1 P(X = 1) = 0.368
(b) For m = 0.5 P(X = 1) = 0.303
(c) For m = 0.5 P(X = 0) = 0.607
(d) For m = 2 P(X = 3) = 0.180
Question
[Maximum mark: 5]
The average number of phone calls in a phone centre is 2 phone calls per minute.
Find
(a) The probability of exactly 3 phone calls in one minute. [1]
(b) The probability of at most 3 phone calls in one minute. [2]
(c) The probability of at least 3 phone calls in one minute. [2]
▶️Answer/Explanation
Answer:
(a) For m = 2 P(X = 3) = 0.180
(b) For m = 2 P(X ≤ 3) = 0.857
(c) For m = 2 P(X ≥ 3) = 0.323
