Question 14. [Maximum mark: 6]
The weights of apples from Tony’s farm follow a normal distribution with mean 158 g and standard deviation 13 g. The apples are sold in bags that contain six apples.
( a ) Find the mean weight of a bag of apples. [2]
(b) Find the standard deviation of the weights of these bags of apples. [2]
(c) Find the probability that a bag selected at random weighs more than 1 kg. [2]
▶️Answer/Explanation
(a) \(158\times 6 = 948 (g) (b) variance 6 \times 13^{2}SD = 31.8 (g (13\sqrt{6}31.8433…..)\) (c) X – N (948,31.8433…)P(X>1000)= 0.0512(0.0512350..)
[MAI 4.11] NORMAL DISTRIBUTION-loyola
Question
[Maximum mark: 7]
The random variable X is normally distributed with μ = 100 and σ = 20, i.e. N(100,202).
(a) Find the probabilities
(i) P(X < 90)
(ii) P(90 < X <130)
(iii) P(X >130) [3]
(b) Sketch a diagram to represent the information in question (a). [2]
(c) 90 is m standard deviations below the mean and 130 is n standard deviations above the mean. Write down the values of m and n. [2]
▶️Answer/Explanation
Answer:
(a) P(X < 90) = 0.308 P(90 < X < 130) = 0.625 P(X > 130) = 0.067
(b)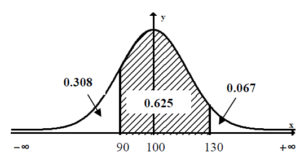
(c) (Standardized values) m = -0.5, n = 1.5
Question
[Maximum mark: 7]
The random variable X follows a normal distribution with μ = 100 and σ = 20.
(a) Given that P(X < a) = 0.8 find the value of a. [2]
(b) Given that P(X > b) = 0.3 find the value of b. [2]
(c) Find Q 1 and Q 3. [3]
▶️Answer/Explanation
Answer:
(a) (use tail left, area 0.8) a = 116.8
(b) (use tail right, area 0.3) b=110.5
(c) (use tail central, area 0.5) Q1 =86.5 and Q3 = 113.5
Question
[Maximum mark: 6]
The random variable X is normally distributed with μ = 100. It given that P(X > 130) = 0.2
Write down the values of the following probabilities
(a) P(X < 130) [1]
(b) P(X < 70) [2]
(c) P(100<X < 130) [1]
(d) P(70<X < 130) [2]
▶️Answer/Explanation
Answer:
(a) P(X < 130) = 0.8
(b) P(X < 70) = 0.2
(c) P(100<X < 130) = 0.3
(d) P(70<X < 130) = 0.6
Question
[Maximum mark: 9]
The mass of packets of a breakfast cereal is normally distributed with a mean of 750 g and standard deviation of 25 g.
(a) Find the probability that a packet chosen at random has mass
(i) less than 740 g; (ii) at least 780 g; (iii) between 740 g and 780 g. [5]
(b) Two packets are chosen at random. What is the probability that both packets
have a mass which is less than 740 g? [2]
(c) The mass of 70% of the packets is more than x grams. Find the value of x. [2]
▶️Answer/Explanation
Answer:
(a) M ~ N (750, 625)
(i) P (M < 740 g) = 0.345
(ii) P (M > 780 g) = 0.115
(iii) P(740 < M < 780) = 0.540
(b) P (both < 740) = 0.3452= 0.119
(c) x = 737 g
