Question
The following Argand diagram shows a circle centre 0 with a radius of 4 units.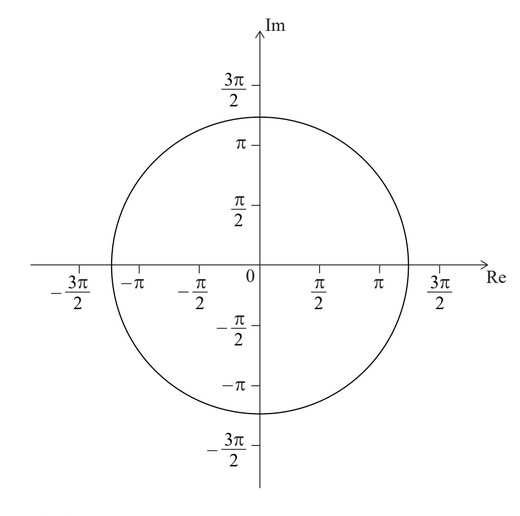
A set of points, \({z_{\theta}}\), on the Argand plane are defined by the equation
\(z_{\theta} =\frac{1}{2} \theta e^{\theta i}\), where \(\theta \geq 0\).
(a) Plot on the Argand diagram the points corresponding to
(i) \(\theta = \frac{\pi}{2}\).
(ii) \(\theta = \pi\)
(ii) \(\theta = \frac{3 \pi}{2}\)
Consider the case where \(|z_{\theta} |=4\).
(b) (i) Find the value of \(\theta\).
(ii) For this value of \(\theta\), plot the approximate position of \(z_{\theta}\) on the Argand diagram.
▶️Answer/Explanation
Ans:
(a)
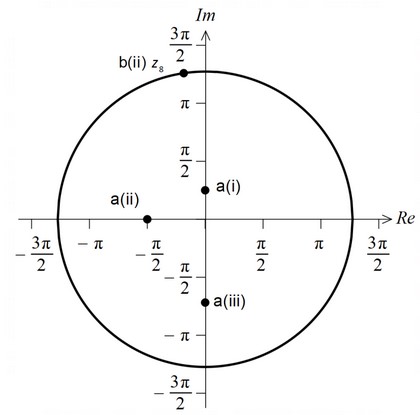
(b) (i) \(\frac{1}{2} \theta = 4\)
\(\Rightarrow \theta = 8\)
(ii) \(z_8\) is shown in the diagram above
Question
Consider \(w = 2\left( {{\text{cos}}\frac{\pi }{3} + {\text{i}}\,{\text{sin}}\frac{\pi }{3}} \right)\)
These four points form the vertices of a quadrilateral, Q.
a.i.Express w2 and w3 in modulus-argument form.[3]
a.ii.Sketch on an Argand diagram the points represented by w0 , w1 , w2 and w3.[2]
b.Show that the area of the quadrilateral Q is \(\frac{{21\sqrt 3 }}{2}\).[3]
c.Let \(z = 2\left( {{\text{cos}}\frac{\pi }{n} + {\text{i}}\,{\text{sin}}\frac{\pi }{n}} \right),\,\,n \in {\mathbb{Z}^ + }\). The points represented on an Argand diagram by \({z^0},\,\,{z^1},\,\,{z^2},\, \ldots \,,\,\,{z^n}\) form the vertices of a polygon \({P_n}\).
Show that the area of the polygon \({P_n}\) can be expressed in the form \(a\left( {{b^n} – 1} \right){\text{sin}}\frac{\pi }{n}\), where \(a,\,\,b\, \in \mathbb{R}\).[6]
▶️Answer/Explanation
Markscheme
\({w^2} = 4\text{cis}\left( {\frac{{2\pi }}{3}} \right){\text{;}}\,\,{w^3} = 8{\text{cis}}\left( \pi \right)\) (M1)A1A1
Note: Accept Euler form.
Note: M1 can be awarded for either both correct moduli or both correct arguments.
Note: Allow multiplication of correct Cartesian form for M1, final answers must be in modulus-argument form.
[3 marks]
A1A1
[2 marks]
use of area = \(\frac{1}{2}ab\,\,{\text{sin}}\,C\) M1
\(\frac{1}{2} \times 1 \times 2 \times {\text{sin}}\frac{\pi }{3} + \frac{1}{2} \times 2 \times 4 \times {\text{sin}}\frac{\pi }{3} + \frac{1}{2} \times 4 \times 8 \times {\text{sin}}\frac{\pi }{3}\) A1A1
Note: Award A1 for \(C = \frac{\pi }{3}\), A1 for correct moduli.
\( = \frac{{21\sqrt 3 }}{2}\) AG
Note: Other methods of splitting the area may receive full marks.
[3 marks]
\(\frac{1}{2} \times {2^0} \times {2^1} \times {\text{sin}}\frac{\pi }{n} + \frac{1}{2} \times {2^1} \times {2^2} \times {\text{sin}}\frac{\pi }{n} + \frac{1}{2} \times {2^2} \times {2^3} \times {\text{sin}}\frac{\pi }{n} + \, \ldots \, + \frac{1}{2} \times {2^{n – 1}} \times {2^n} \times {\text{sin}}\frac{\pi }{n}\) M1A1
Note: Award M1 for powers of 2, A1 for any correct expression including both the first and last term.
\( = {\text{sin}}\frac{\pi }{n} \times \left( {{2^0} + {2^2} + {2^4} + \, \ldots \, + {2^{n – 2}}} \right)\)
identifying a geometric series with common ratio 22(= 4) (M1)A1
\( = \frac{{1 – {2^{2n}}}}{{1 – 4}} \times {\text{sin}}\frac{\pi }{n}\) M1
Note: Award M1 for use of formula for sum of geometric series.
\( = \frac{1}{3}\left( {{4^n} – 1} \right){\text{sin}}\frac{\pi }{n}\) A1
[6 marks]
Question
If \({z_1} = a + a\sqrt 3 i\) and \({z_2} = 1 – i\), where a is a real constant, express \({z_1}\) and \({z_2}\) in the form \(r\,{\text{cis}}\,\theta \), and hence find an expression for \({\left( {\frac{{{z_1}}}{{{z_2}}}} \right)^6}\) in terms of a and i.
▶️Answer/Explanation
Markscheme
\({z_1} = 2a{\text{cis}}\left( {\frac{\pi }{3}} \right){\text{, }}{z_2} = \sqrt 2 {\text{ cis}}\left( { – \frac{\pi }{4}} \right)\) M1 A1 A1
EITHER
\({\left( {\frac{{{z_1}}}{{{z_2}}}} \right)^6} = \frac{{{2^6}{a^6}{\text{cis(0)}}}}{{{{\sqrt 2 }^6}{\text{cis}}\left( {\frac{\pi }{2}} \right)}}\left( { = 8{a^6}{\text{cis}}\left( { – \frac{\pi }{2}} \right)} \right)\) M1 A1 A1
OR
\({\left( {\frac{{{z_1}}}{{{z_2}}}} \right)^6} = {\left( {\frac{{2a}}{{\sqrt 2 }}{\text{cis}}\left( {\frac{{7\pi }}{{12}}} \right)} \right)^6}\) M1 A1
\( = 8{a^6}{\text{cis}}\left( { – \frac{\pi }{2}} \right)\) A1
THEN
\( = – 8{a^6}{\text{i}}\) A1
Note: Accept equivalent angles, in radians or degrees.
Accept alternate answers without cis e.g. \({\text{ = }}\frac{{8{a^6}}}{{\text{i}}}\)
[7 marks]
Question
Given the complex numbers \({z_1} = 1 + 3{\text{i}}\) and \({z_2} = – 1 – {\text{i}}\).
a.Write down the exact values of \(\left| {{z_1}} \right|\) and \(\arg ({z_2})\).[2]
b.Find the minimum value of \(\left| {{z_1} + \alpha{z_2}} \right|\), where \(\alpha \in \mathbb{R}\).[5]
▶️Answer/Explanation
Markscheme
\(\left| {{z_1}} \right| = \sqrt {10} ;{\text{ }}\arg ({z_2}) = – \frac{{3\pi }}{4}{\text{ }}\left( {{\text{accept }}\frac{{5\pi }}{4}} \right)\) A1A1
[2 marks]
\(\left| {{z_1} + \alpha{z_2}} \right| = \sqrt {{{(1 – \alpha )}^2} + {{(3 – \alpha )}^2}} \) or the squared modulus (M1)(A1)
attempt to minimise \(2{\alpha ^2} – 8\alpha + 10\) or their quadratic or its half or its square root M1
obtain \(\alpha = 2\) at minimum (A1)
state \(\sqrt 2 \) as final answer A1
[5 marks]
