IB Mathematics AHL 2.8 Transformations of graphs AI HL Paper 1- Exam Style Questions- New Syllabus
The following diagram shows the graph of \( y = \arctan(2x + 1 + \frac{\pi}{4}) \) for \( x \in \mathbb{R} \) with asymptotes at \( y = -\frac{\pi}{4} \) and \( y = \frac{3\pi}{4} \).
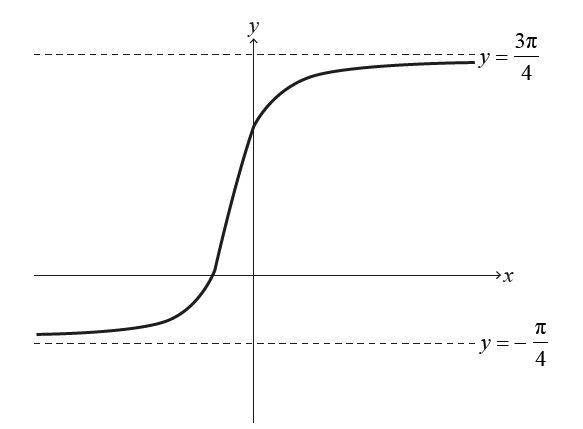
(a) Describe a sequence of transformations that transforms the graph of \( y = \arctan x \) to the graph of \( y = \arctan(2x + 1 + \frac{\pi}{4}) \) for \( x \in \mathbb{R} \).
(b) Show that \( \arctan p + \arctan q = \arctan \left( \frac{p + q}{1 – p q} \right) \) where \( p, q > 0 \) and \( p q < 1 \).
(c) Verify that \( \arctan(2x + 1) = \arctan \left( \frac{x}{x + 1} \right) + \frac{\pi}{4} \) for \( x \in \mathbb{R} \), \( x > 0 \).
(d) Using mathematical induction and the result from part (b), prove that \( \sum_{r=1}^{n} \arctan \left( \frac{1}{2r^2} \right) = \arctan \left( \frac{n}{n + 1} \right) \) for \( n \in \mathbb{Z}^+ \).
▶️ Answer/Explanation
(a)
Transform \( y = \arctan x \) to \( y = \arctan(x + 1) \): translation of 1 unit left (A1)
Then to \( y = \arctan(2x + 1) \): horizontal stretch by scale factor \( \frac{1}{2} \) (A1)
Then to \( y = \arctan(2x + 1 + \frac{\pi}{4}) \): vertical translation \( \frac{\pi}{4} \) units up (A1)
Result: Translation 1 unit left, horizontal stretch by \( \frac{1}{2} \), vertical translation \( \frac{\pi}{4} \) up [3]
(b)
Take tangent of both sides: \( \tan(\arctan p + \arctan q) = \tan \left( \arctan \left( \frac{p + q}{1 – p \times q} \right) \right) \) (M1)
Left: \( \tan(\arctan p + \arctan q) = \frac{\tan(\arctan p) + \tan(\arctan q)}{1 – \tan(\arctan p) \times \tan(\arctan q)} = \frac{p + q}{1 – p \times q} \) (A1)
Right: \( \tan \left( \arctan \left( \frac{p + q}{1 – p \times q} \right) \right) = \frac{p + q}{1 – p \times q} \) (A1)
Since both sides equal, identity holds for \( p, q > 0 \), \( p \times q < 1 \) (A1)
Result: \( \arctan p + \arctan q = \arctan \left( \frac{p + q}{1 – p \times q} \right) \) [4]
(c)
Right: \( \arctan \left( \frac{x}{x + 1} \right) + \frac{\pi}{4} = \arctan \left( \frac{x}{x + 1} \right) + \arctan 1 \) (M1)
Use (b): \( \arctan \left( \frac{x}{x + 1} \right) + \arctan 1 = \arctan \left( \frac{\frac{x}{x + 1} + 1}{1 – \frac{x}{x + 1} \times 1} \right) = \arctan \left( \frac{\frac{x + x + 1}{x + 1}}{\frac{x + 1 – x}{x + 1}} \right) \) (A1)
Simplify: \( \arctan \left( \frac{2x + 1}{1} \right) = \arctan(2x + 1) \) (A1)
Result: Left = \( \arctan(2x + 1) \), verified [3]
(d)
Prove \( \sum_{r=1}^{n} \arctan \left( \frac{1}{2r^2} \right) = \arctan \left( \frac{n}{n + 1} \right) \) by induction.
Base case (\( n = 1 \)): \( \arctan \left( \frac{1}{2} \right) = \arctan \left( \frac{1}{2} \right) \), true (A1)
Assume true for \( n = k \): \( \sum_{r=1}^{k} \arctan \left( \frac{1}{2r^2} \right) = \arctan \left( \frac{k}{k + 1} \right) \) (M1)
Prove for \( n = k + 1 \): \( \sum_{r=1}^{k+1} \arctan \left( \frac{1}{2r^2} \right) = \arctan \left( \frac{k}{k + 1} \right) + \arctan \left( \frac{1}{2(k + 1)^2} \right) \) (M1)
Use (b): \( \arctan \left( \frac{\frac{k}{k + 1} + \frac{1}{2(k + 1)^2}}{1 – \frac{k}{k + 1} \times \frac{1}{2(k + 1)^2}} \right) = \arctan \left( \frac{2k(k + 1)^2 + 1}{2(k + 1)^3 – k} \right) \) (A1)
Simplify: \( \frac{(k + 1)(2k^2 + 2k + 1)}{(k + 2)(2k^2 + 2k + 1)} = \frac{k + 1}{k + 2} \), so \( \arctan \left( \frac{k + 1}{k + 2} \right) \) (A1)
By induction, true for all \( n \in \mathbb{Z}^+ \) (A1)
Result: \( \sum_{r=1}^{n} \arctan \left( \frac{1}{2r^2} \right) = \arctan \left( \frac{n}{n + 1} \right) \) [6]
