Question
The graphs of y = 6 – x and \(y=1.5x^2 – 2.5x + 3\) intersect at (2, 4) and (-1, 7), as shown the following diagrams.
In diagram 1, the region enclosed by the line y = 6-x, x = -1, x = 2 and the x-axis has been shaded.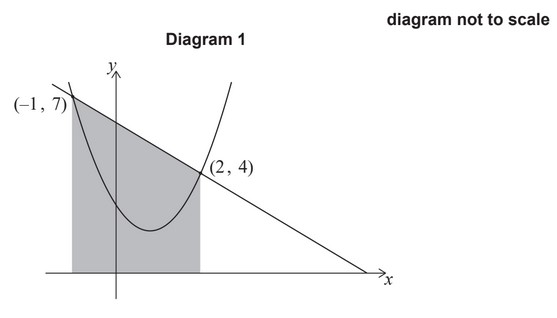
(a) Calculate the area of the shaded region in diagram 1.
In diagram 2, the region enclosed by the curve \(y = 1.5x^2 – 2.5x + 3\), and teh lines x = -1, x = 2 and the x-axis has been shaded.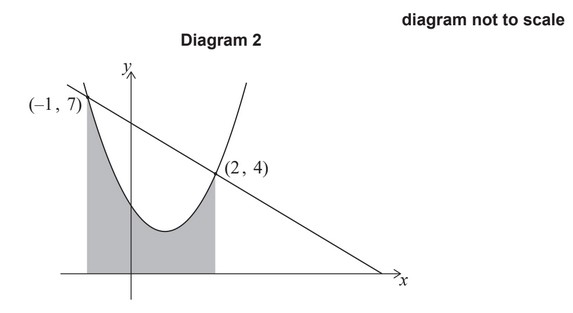
(b) (i) Write down an integral for the area of the shaded region in diagram 2.
(ii) Calculate the area of this region.
(c) Hence, determine the area enclosed between y = 6 -x and \(y = 1.5x^2 – 2.5x + 3\).
▶️Answer/Explanation
Ans:
(a) EITHER
attempt to substitute 3, 4 and 7 into area of a trapezoid formula
\((A+)\frac{1}{2} (7+4)(3)\)
OR
given area expressed as an integral
\((A=)\int_{-1}^{2}(6-x)dx\)
OR
attempt to sum area of rectangle and area of triangle
\((A=) 4 \times 3 + \frac{1}{2} (3)(3)\)
THEN
16.5 (square units)
(b) (i) \((A=)\int_{-1}^{2} 1.5x^2 – 2.5x + 3dx\)
(ii) 9.75 (square units)
(c) 16.5 – 9.75
6.75 (square units)
Question
(a) (i) Expand \((\frac{1}{u} + 1)^2\).
(ii) Find \(\int (\frac{1}{x+2}+1)^2 dx\).
The region bounded by \(y = \frac{1}{(x+2)}+1\), x = 0, x = 2 and the x-axis is rotated through \(2\pi\) about the x-axis to form a solid.
(b) Find the volume of the solid formed. Give your answer in the fomr \(\frac{\pi}{4}(a+b In (c))\), where \(a, b , c\epsilon \mathbb{Z}\).
▶️Answer/Explanation
Ans:
(a) (i) \(\frac{1}{u^2}+\frac{2}{u}+1\)
(ii) \(\int (\frac{1}{(x+2)}+1)^2dx
=\int (\frac{1}{(x+2)^2}+\frac{2}{x+2}+1)dx OR \int (\frac{1}{u^2}+\frac{2}{u})du
=-\frac{1}{(x+2)} + 2 In |x+2| + x(+c)\)
Question
A particle moves in a straight line. The velocity, v ms–1 , of the particle at time t seconds is given by v (t) = t sint – 3 , for 0 ≤ t ≤ 10.
The following diagram shows the graph of v .
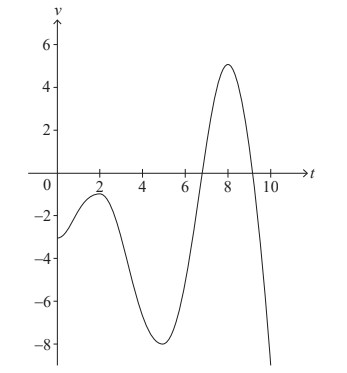
Find the smallest value of t for which the particle is at rest. [2]
Find the total distance travelled by the particle. [2]
Find the acceleration of the particle when t = 7 . [2]
▶️Answer/Explanation
Ans:
(a) recognising v=o t = 6.74416… = 6.74 (sec)
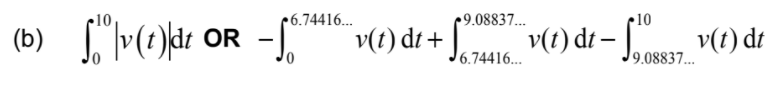= 37.0968… = 37.1 (m)
(c) recognising acceleration at t = 7 is given by v’ (7) acceleration = 5.93430… = 5.93 (ms-2)
Question
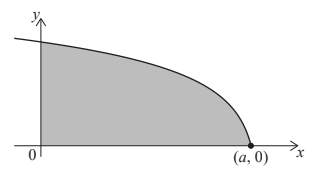
Let f (x) = \(\sqrt{12-2x}\) , x ≤ a . The following diagram shows part of the graph of f .
The shaded region is enclosed by the graph of f , the x-axis and the y-axis.
x
The graph of f intersects the x-axis at the point (a , 0) .
Find the value of a . [2]
Find the volume of the solid formed when the shaded region is revolved 360° about the x-axis. [5]
▶️Answer/Explanation
Ans:
(a)
recognize f (x) = 0
eg \(\sqrt{12-2x}= 0, 2x=12\)
a= 6 (accept x= 6, (6,0))
(b)
attempt to substitute either their limits or the function into volume formula (must involve \(f^{2})\)
eg \(\int_{0}^{6}f^{2}dx , \pi \int (\sqrt{12-2x})^{2}, \pi \int_{0}^{6}\)(12-2x) dx
correct integaration of each term
eg \(12x-x^{2}, 12x-x^{2}\)+c, \(\left [ 12x-x^{2} \right ]_0^6\)
substituting limits into their integrated function and subtracting (in any order)
eg \(\pi (12(6)-(6)^{2})-\pi (0),72\pi -36\pi ,(12(6)-(6)^{2})-(0)\)
volume = \(36\pi \)
Question
a.Find \(\int {\frac{1}{{2x + 3}}} {\rm{d}}x\) .[2]
b.Given that \(\int_0^3 {\frac{1}{{2x + 3}}} {\rm{d}}x = \ln \sqrt P \) , find the value of P.[4]
▶️Answer/Explanation
Markscheme
\(\int {\frac{1}{{2x + 3}}} {\rm{d}}x = \frac{1}{2}\ln (2x + 3) + C\) (accept \(\frac{1}{2}\ln |(2x + 3)| + C\) ) A1A1 N2
[2 marks]
\(\int_0^3 {\frac{1}{{2x + 3}}} {\rm{d}}x = \left[ {\frac{1}{2}\ln (2x + 3)} \right]_0^3\)
evidence of substitution of limits (M1)
e.g.\(\frac{1}{2}\ln 9 – \frac{1}{2}\ln 3\)
evidence of correctly using \(\ln a – \ln b = \ln \frac{a}{b}\) (seen anywhere) (A1)
e.g. \(\frac{1}{2}\ln 3\)
evidence of correctly using \(a\ln b = \ln {b^a}\) (seen anywhere) (A1)
e.g. \(\ln \sqrt {\frac{9}{3}} \)
\(P = 3\) (accept \(\ln \sqrt 3 \) ) A1 N2
[4 marks]