Question
The position vector of a particle, P, relative to a fixed origin O at time t is given by
\(\overrightarrow{OP} = \binom{sin(t^2)}{cos(t^2)}\).
(a) Find the velocity vector of P.
(b) Show that the acceleration vector of P is never parallel to the position vector of P.
▶️Answer/Explanation
Ans:
(a) attempt at chain rule
\(\begin{pmatrix}
v=\frac{dOP}{dt}
\end{pmatrix}\begin{pmatrix}
2t cos t^2\\
-2t sin t^2
\end{pmatrix}\)
(b) attempt at product rule
\(a=\begin{pmatrix}
2 cos t^2 – 4t^2 sin t^2\\
-2 sin t^2 – 4t^2 cos t^2
\end{pmatrix}\)
METHOD 1
let \(S= sin t^2\) and \(C = cos t^2\)
finding cos \(\theta \) using
\(a. \overrightarrow{OP} = 2SC – 4t^2 S^2 – 2SC – 4t^2C^2 = – 4t^2\)
\(|\overrightarrow{OP}| = 1\)
\(|a| = \sqrt{(2C-4t^2S)^2 + (-2S – 4t^2 C)^2}\)
\(=\sqrt{4 + 16t^4}> 4t^2\)
it \(\theta\) is the angle between them, then
\(cos \theta = -\frac{4t^2}{\sqrt{4+16t^4}}\)
so -1 < cos \(\theta\) < 0 therefore the vectors are never parallel
METHOD 2
solve
\(\begin{pmatrix}
2cos t^2 – 4t^2 sin t^2\\ -2 sin t^2 – 4t^2 cos t^2
\end{pmatrix} = k \binom{sin t^2}{cos t^2}\)
then
\((k=) \frac{2cos t^2 – 4t^2 sin t^2}{sin t^2} = \frac{-2 sin t^2 – 4t^2 cos t^2}{cos t^2}\)
\(2cos^2 t^2 – 4t^2 cos t^2 sin t^2 = -2 sin^2 t^2 – 4t^2 cos t^2 sin t^2\)
\(2cos^2 t^2 + 2 sin^2 t^2 =0\)
2 = 0
this is never true so the two vectors are never parallel
MEHTOD 3
embedding vectors in a 3d space and taking the cross product.
\(\begin{pmatrix}
sin t^2\\ cos t^2
\\ 0
\end{pmatrix} \times \begin{pmatrix}
2 cos t^2-4t^2 sin t^2\\-2 sin t^2 – 4t^2 cos t^2
\\ 0
\end{pmatrix} = \begin{pmatrix}
0\\0
\\ -2sin^2t^2 – 4t^2 cos t^2 sin t^2 – 2 cos^2 t^2 + 4t^2 cos t^2 sin t^2
\end{pmatrix}\)
\(=\begin{pmatrix}
0\\0
\\ -2
\end{pmatrix}\)
since the cross product is never zero, the two vectors are never parallel
Question
5. A ball is dropped from a height of 1.8 metres and bounces on the ground. The maximum
height reached by the ball, after each bounce, is 85% of the previous maximum height.
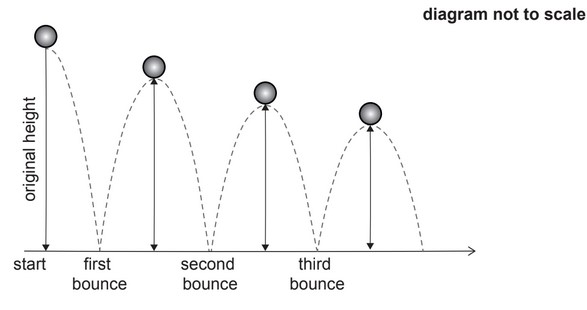
(a) Show that the maximum height reached by the ball after it has bounced for the sixth
time is 68cm, to the nearest cm.
(b) Find the number of times, after the first bounce, that the maximum height reached is
greater than 10cm.
(c) Find the total vertical distance travelled by the ball from the point at which it is dropped
until the fourth bounce.
▶️Answer/Explanation
Ans:
(a) use of geometric sequence with r = 0.85
EITHER
\((0.85)^6(1.8)\) OR 0.678869… OR \((0.85)^5 (1.53)\)
= 0.68m
= 68 cm
OR
\((0.85)^6(180)\) OR \((0.85)^5(153)\)
= 68 cm
(b) EITHER
\((0.85)^n (1.8) > 0.1\) OR \((0.85)^{n-1}(1.53)>0.1\)
17
OR
\((0.85)^{17}(1.8 = 0.114m\) and \((0.85)^{18}(1.8)=0.0966m\)
17
OR
solving \((0.85)^n(1.8)=0.1\) to find n = 17.8
17
(c) EITHER
distance (in one direction) travelled between first and fourth bounce
\(=\frac{(1.8 \times 0.86)(1-0.85^3)}{1-0.85}(=3.935925)\)
recognizing distances are travelled twice except first distance
1.8 + 2 (3.935925)
= 9.67 m (9.67185…m)
OR
distance (in one direction) travelled between drop and fourth bounce
\(=\frac{(1.8)(1-0.85^4)}{1-0.85}(=5.735925)\)
recognizing distances are travelled twice except first distance
2(5.735925)-1.8
= 9.67m (9.67185…m)
OR
distance (in one direction) travelled between first and fourth bounce
\((0.85)(1.8)+(0.85)^2(1.8) (=3.935925…)\)
recognizing distances are travelled twice except first distance
\(1.8+2(0.85)(1.8)+2(0.85)^2(1.8)+2(0.85)^3(1.8)\)
= 9.67m (9.67185…m)
Question
The acceleration, a ms-2 , of a particle moving in a horizontal line at time t seconds, t ≥ 0 , is given by a = – (1+v) where v ms-1 is the particle’s velocity and v > -1.
At t = 0 , the particle is at a fixed origin O and has initial velocity v0 ms-1 .
(a) By solving an appropriate differential equation, show that the particle’s velocity at time t is given by v ( t ) = (1 + v0) e-t – 1 . [6]
(b) Initially at O, the particle moves in the positive direction until it reaches its maximum displacement from O. The particle then returns to O.
Let s metres represent the particle’s displacement from O and smax its maximum displacement from O.
(i) Show that the time T taken for the particle to reach smax satisfies the equation eT = 1 + v0 .
(ii) By solving an appropriate differential equation and using the result from part (b) (i), find an expression for smax in terms of v0 . [7]
Let v (T – k) represent the particle’s velocity k seconds before it reaches smax , where v (T – k) = (1 + v0) e-(T – k) – 1 .
(c) By using the result to part (b) (i), show that v (T – k) = ek – 1 . [2]
Similarly, let v (T + k) represent the particle’s velocity k seconds after it reaches smax .
(d) Deduce a similar expression for v (T + k) in terms of k . [2]
(e) Hence, show that v (T – k) + v (T + k) ≥ 0 . [3]
▶️Answer/Explanation
Ans:
(a) Since $a=\frac{\text{d}v}{\text{d}t}$, and $a=-\left(1+v\right)$, we have
$$\begin{eqnarray}
\frac{\text{d}v}{\text{d}t} = -1-v \nonumber \\
\frac{\text{d}v}{\text{d}t}+v = -1.
\end{eqnarray}$$
Let $\text{I}\left(x\right)=\text{e}^{\int 1 \text{d}t}=\text{e}^t$.<br>
Then, we have
$$\begin{eqnarray}
\frac{\text{d}}{\text{d}t}\left(v\text{e}^t\right) = -\text{e}^t \nonumber \\
v\text{e}^t = -\int\text{e}^t \text{d}t \nonumber \\
v\text{e}^t = -\text{e}^t+c \nonumber \\
v = c\text{e}^{-t}-1.
\end{eqnarray}$$
Since $v=v_0$ when $t=0$, we have $c=1+v_0$, i.e., $v=\left(1+v_0\right)\text{e}^{-t}-1$.<br>
(b)(i) At $s_{\text{max}}$, $t=T$, i.e., we have
$$\begin{eqnarray}
v\left(T\right) = 0 \nonumber \\
\left(1+v_0\right)\text{e}^{-T}-1 = 0 \nonumber \\
\left(1+v_0\right)\text{e}^{-T} = 1 \nonumber \\
1+v_0 = \text{e}^T.
\end{eqnarray}$$
(b)(ii) Since $\frac{\text{d}s}{\text{d}t}=\left(1+v_0\right)\text{e}^{-t}-1$, integrating both sides with respect to $t$, we have
$$\begin{eqnarray}
s &=& \int\left(1+v_0\right)\text{e}^{-t}-1\text{d}t \nonumber \\
&=& -\left(1+v_0\right)\text{e}^{-t}-t+c.
\end{eqnarray}$$
When $t=0$, $s=0$, i.e.,
$$\begin{eqnarray}
0 = -\left(1+v_0\right)+c \nonumber \\
c = \left(1+v_0\right).
\end{eqnarray}$$
Thus, $s=\left(1+v_0\right)-\left(1+v_0\right)\text{e}^{-t}-t$.<br>
Since from (b)(i) we have $1+v_0=\text{e}^T$, $T=\ln\left(1+v_0\right)$, i.e., $s_{\text{max}}=v_0-\ln \left(1+v_0\right)$.<br>
(c) Since $\text{e}^T=1+v_0$, we have $\left(1+v_0\right)\text{e}^{-T}=1$, i.e.,
$$\begin{eqnarray}
v\left(T-k\right) &=& \left(1+v_0\right)\text{e}^{-\left(T-k\right)}-1 \nonumber \\
&=& \left(1+v_0\right)\text{e}^{-T}\text{e}^k-1 \nonumber \\
&=& \text{e}^k-1.
\end{eqnarray}$$
(d) Similarly, as in (c),
$$\begin{eqnarray}
v\left(T+k\right) &=& \left(1+v_0\right)\text{e}^{-\left(T+k\right)}-1 \nonumber \\
&=& \left(1+v_0\right)\text{e}^{-T}\text{e}^{-k}-1 \nonumber \\
&=& \text{e}^{-k}-1.
\end{eqnarray}$$
(e)
$$\begin{eqnarray}
v\left(T-k\right)+v\left(T+k\right) &=& \text{e}^k-1+\text{e}^{-k}-1 \nonumber \\
&=& \text{e}^k+\text{e}^{-k}-2 \nonumber \\
&=& \frac{\text{e}^{2k}-2\text{e}^k+1}{\text{e}^k} \nonumber \\
&=& \frac{\left(\text{e}^k-1\right)^2}{\text{e}^k} \geq 0.
\end{eqnarray}$$
Question
A particle P moves in a straight line with displacement relative to origin given by
\[s = 2\sin (\pi t) + \sin (2\pi t),{\text{ }}t \geqslant 0,\]
where t is the time in seconds and the displacement is measured in centimetres.
(i) Write down the period of the function s.
(ii) Find expressions for the velocity, v, and the acceleration, a, of P.
(iii) Determine all the solutions of the equation v = 0 for \(0 \leqslant t \leqslant 4\).[10]
b.Consider the function
\[f(x) = A\sin (ax) + B\sin (bx),{\text{ }}A,{\text{ }}a,{\text{ }}B,{\text{ }}b,{\text{ }}x \in \mathbb{R}.\]
Use mathematical induction to prove that the\({(2n)^{{\text{th}}}}\) derivative of f is given by \(({f^{(2n)}}(x) = {( – 1)^n}\left( {A{a^{2n}}\sin (ax) + B{b^{2n}}\sin (bx)} \right)\), for all \(n \in {\mathbb{Z}^ + }\).[8]
▶️Answer/Explanation
Markscheme
(i) the period is 2 A1
(ii) \(v = \frac{{{\text{d}}s}}{{{\text{d}}t}} = 2\pi \cos (\pi t) + 2\pi \cos (2\pi t)\) (M1)A1
\(a = \frac{{{\text{d}}v}}{{{\text{d}}t}} = – 2{\pi ^2}\sin (\pi t) – 4{\pi ^2}\sin (2\pi t)\) (M1)A1
(iii) \(v = 0\)
\(2\pi \left( {\cos (\pi t) + \cos (2\pi t)} \right) = 0\)
EITHER
\(\cos (\pi t) + 2{\cos ^2}(\pi t) – 1 = 0\) M1
\(\left( {2\cos (\pi t) – 1} \right)\left( {\cos (\pi t) + 1} \right) = 0\) (A1)
\(\cos (\pi t) = \frac{1}{2}{\text{ or }}\cos (\pi t) = – 1\) A1
\(t = \frac{1}{3},{\text{ }}t = 1\) A1
\(t = \frac{5}{3},{\text{ }}t = \frac{7}{3},{\text{ }}t = \frac{{11}}{3},{\text{ }}t = 3\) A1
OR
\(2\cos \left( {\frac{{\pi t}}{2}} \right)\cos \left( {\frac{{3\pi t}}{2}} \right) = 0\) M1
\(\cos \left( {\frac{{\pi t}}{2}} \right) = 0{\text{ or }}\cos \left( {\frac{{3\pi t}}{2}} \right) = 0\) A1A1
\(t = \frac{1}{3},{\text{ 1}}\) A1
\(t = \frac{5}{3},{\text{ }}\frac{7}{3},{\text{ }}3,{\text{ }}\frac{{11}}{3}\) A1
[10 marks]
\(P(n):{f^{(2n)}}(x) = {( – 1)^n}\left( {A{a^{2n}}\sin (ax) + B{b^{2n}}\sin (bx)} \right)\)
\(P(1):f”(x) = {\left( {Aa\cos (ax) + Bb\cos (bx)} \right)^\prime }\) M1
\( = – A{a^2}\sin (ax) – B{b^2}\sin (bx)\)
\( = – 1\left( {A{a^2}\sin (ax) + B{b^2}\sin (bx)} \right)\) A1
\(\therefore P(1)\) true
assume that
\(P(k):{f^{(2k)}}(x) = {( – 1)^k}\left( {A{a^{2k}}\sin (ax) + B{b^{2k}}\sin (bx)} \right)\) is true M1
consider \(P(k + 1)\)
\({f^{(2k + 1)}}(x) = {( – 1)^k}\left( {A{a^{2k + 1}}\cos (ax) + B{b^{2k + 1}}\cos (bx)} \right)\) M1A1
\({f^{(2k + 2)}}(x) = {( – 1)^k}\left( { – A{a^{2k + 2}}\sin (ax) – B{b^{2k + 2}}\sin (bx)} \right)\) A1
\( = {( – 1)^{k + 1}}\left( {A{a^{2k + 2}}\sin (ax) + B{b^{2k + 2}}\sin (bx)} \right)\) A1
\(P(k)\) true implies \(P(k + 1)\) true, \(P(1)\) true so \(P(n)\) true \(\forall n \in {\mathbb{Z}^ + }\) R1
Note: Award the final R1 only if the previous three M marks have been awarded.
[8 marks]
Examiners report
In (a), only a few candidates gave the correct period but the expressions for velocity and acceleration were correctly obtained by most candidates. In (a)(iii), many candidates manipulated the equation v = 0 correctly to give the two possible values for \(\cos (\pi t)\) but then failed to find all the possible values of t.
Solutions to (b) were disappointing in general with few candidates giving a correct solution.
Question
A body is moving in a straight line. When it is \(s\) metres from a fixed point O on the line its velocity, \(v\), is given by \(v = – \frac{1}{{{s^2}}},{\text{ }}s > 0\).
Find the acceleration of the body when it is 50 cm from O.
▶️Answer/Explanation
Markscheme
\(\frac{{{\text{d}}v}}{{{\text{d}}s}} = 2{s^{ – 3}}\) M1A1
Note: Award M1 for \(2{s^{ – 3}}\) and A1 for the whole expression.
\(a = v\frac{{{\text{d}}v}}{{{\text{d}}s}}\) (M1)
\(a = – \frac{1}{{{s^2}}} \times \frac{2}{{{s^3}}}\left( { = – \frac{2}{{{s^5}}}} \right)\) (A1)
when \(s = \frac{1}{2},{\text{ }}a = – \frac{2}{{{{(0.5)}^5}}}{\text{ }}( = – 64){\text{ (m}}{{\text{s}}^{ – 2}})\) M1A1
Note: M1 is for the substitution of 0.5 into their equation for acceleration.
Award M1A0 if \(s = 50\) is substituted into the correct equation.
[6 marks]
