IB Mathematics AHL 5.16 first order differential equations AI HL Paper 1- Exam Style Questions- New Syllabus
Question
\(\frac{dx}{dt} = 3x – 2y\)
\(\frac{dy}{dt} = 4x – y\)
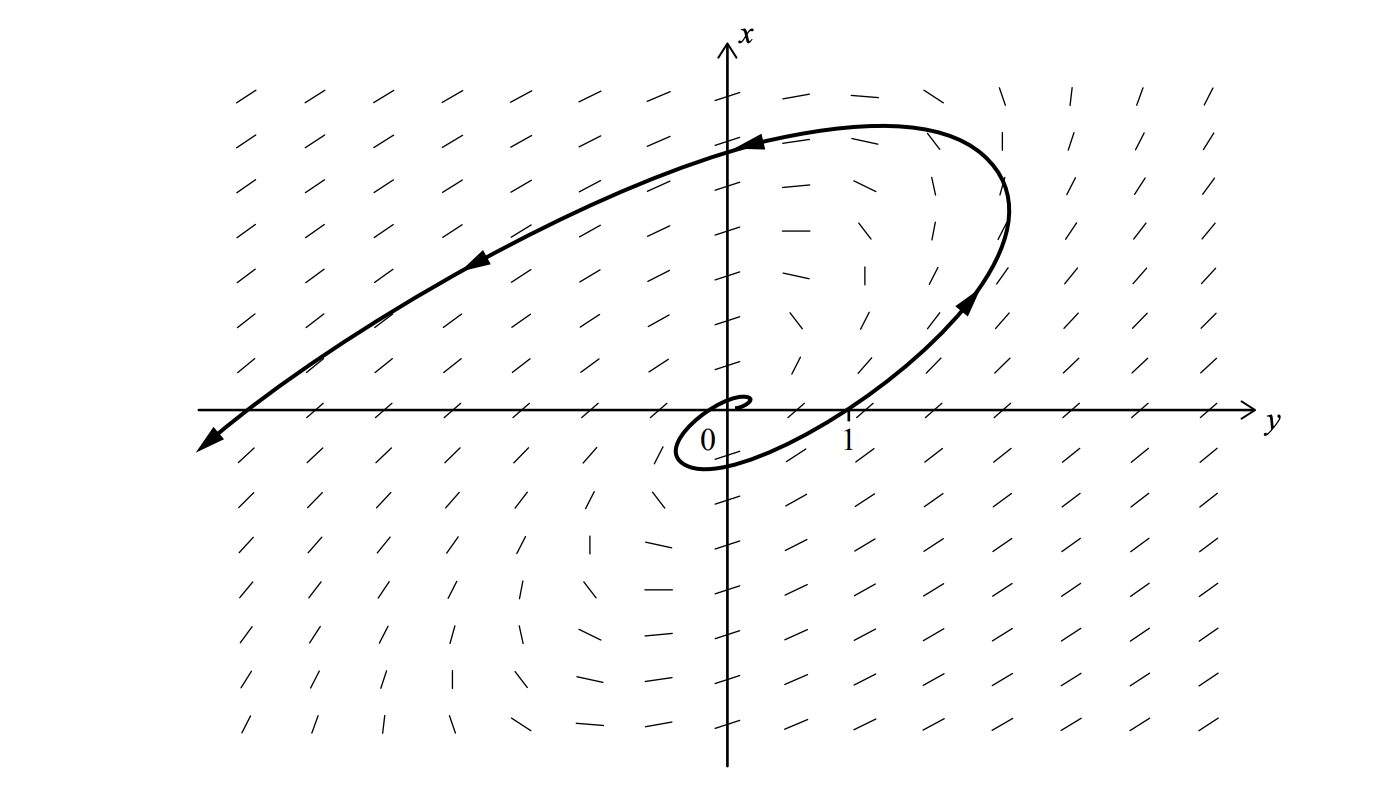
(a) Based on the characteristics of the phase portrait, identify which of the following could be an eigenvalue for this system.
- A. \(1\)
- B. \(2i\)
- C. \(1+2i\)
- D. \(-1+2i\)
Most-appropriate topic codes:
• AHL 5.16: Numerical solution of the coupled system by Euler’s method — part (b)
▶️ Answer/Explanation
(a)
The phase portrait displays a trajectory spiraling away from the origin (a spiral source). This behavior indicates that the system’s eigenvalues must be complex with a positive real part. Therefore, the correct option is C (\(1+2i\)).
(b)
We apply Euler’s method for coupled systems using the initial conditions \(t_0=5, x_0=1, y_0=0\) and step size \(h=0.1\). The iterative formulas are:
\(x_{n+1} = x_n + 0.1(3x_n – 2y_n)\)
\(y_{n+1} = y_n + 0.1(4x_n – y_n)\)
| \(n\) | \(t\) | \(x\) | \(y\) |
|---|---|---|---|
| \(0\) | \(5\) | \(1\) | \(0\) |
| \(1\) | \(5.1\) | \(1.3\) | \(0.4\) |
| \(2\) | \(5.2\) | \(1.61\) | \(0.88\) |
| \(3\) | \(5.3\) | \(1.917\) | \(1.436\) |
| \(4\) | \(5.4\) | \(2.2049\) | \(2.0592\) |
For the final step to \(t=5.5\):
\(x = 2.2049 + 0.1(3(2.2049) – 2(2.0592)) \approx 2.45453\dots\)
\(y = 2.0592 + 0.1(4(2.2049) – 2.0592) \approx 2.73524\dots\)
Estimated values at \(t=5.5\):
\(x \approx 2.45\)
\(y \approx 2.74\)
