Question
The wind chill index W is a measure of the temperature, in \(^∘C\), felt when taking into account the effect of the wind.
When Frieda arrives at the top of a hill, the relationship between the wind chill index and the speed of the wind v in kilometres per hour \((km h^{-1}\)) is given by equation
\(W = 19.34 – 7.405 v^{0.16}\)
(a) Find an expression for \(\frac{dW}{dv}\).
When Frieda arrives at the top of a hill, the speed of the wind is 10 kilometres per hour and increasing at a rate of \(5kmh^{-1} minute^{-1}\).
(b) Find the rate of change of W at this time.
▶️Answer/Explanation
Ans:
(a) use of power rule
\(\frac{dW}{dv} = -1848v^{-0.84}\) OR \(-1.18v^{-0.84}\)
(b) \(\frac{dv}{dt}=5\)
\(\frac{dW}{dt}=\frac{dv}{dt} \times \frac{dW}{dv}\)
\((\frac{dW}{dt}=-5 \times 1.1848v^{-0.84}\))
when v = 10
\(\frac{dW}{dt} = -5 \times 1.1848 \times 10^{-0.84}\)
– 0.856 (-0.856278…) \(^oC min^{-1}\)
Question
Consider the curve \(y = 2x(4- e^x)\).
(a) Find
(i) \(\frac{dy}{dx}\).
(ii) \(\frac{d^2y}{dx^2}\).
The curve has a point of inflexion at (a, b).
(b) Find the value of a.
▶️Answer/Explanation
Ans:
(a) (i) use of product
\(\frac{dy}{dx}=2(4-e^x)+2x(-e^x)\)
\(=8 – 2e^x – 2xe^x\)
(ii) use of product rule
\(\frac{d^2y}{dx^2}=-2e^x – 2e^x – 2xe^x\)
\(=-4e^x – 2xe^x\)
\(=-2(2+x)e^x\)
(b) \(-2(2+a)e^a = 0\) OR sketch \(\frac{d^2y}{dx^2}\) with x-intercept indicated
OR finding the local maximum of \(\frac{dy}{dx}\) at (-2, 8.27)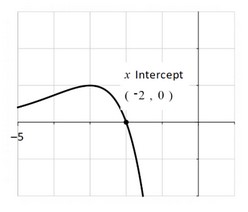
(a=) -2
Question
Consider the curve \(y = 2x(4- e^x)\).
(a) Find
(i) \(\frac{dy}{dx}\).
(ii) \(\frac{d^2y}{dx^2}\).
The curve has a point of inflexion at (a, b).
(b) Find the value of a.
▶️Answer/Explanation
Ans:
(a) (i) use of product
\(\frac{dy}{dx}=2(4-e^x)+2x(-e^x)\)
\(=8 – 2e^x – 2xe^x\)
(ii) use of product rule
\(\frac{d^2y}{dx^2}=-2e^x – 2e^x – 2xe^x\)
\(=-4e^x – 2xe^x\)
\(=-2(2+x)e^x\)
(b) \(-2(2+a)e^a = 0\) OR sketch \(\frac{d^2y}{dx^2}\) with x-intercept indicated
OR finding the local maximum of \(\frac{dy}{dx}\) at (-2, 8.27)
(a=) -2
Question
Consider the function \(f(x) = \frac{{\ln x}}{x}\) , \(0 < x < {{\text{e}}^2}\) .
a.(i) Solve the equation \(f'(x) = 0\) .
(ii) Hence show the graph of \(f\) has a local maximum.
(iii) Write down the range of the function \(f\) .[5]
b.Show that there is a point of inflexion on the graph and determine its coordinates.[5]
c.Sketch the graph of \(y = f(x)\) , indicating clearly the asymptote, x-intercept and the local maximum.[3]
d.Now consider the functions \(g(x) = \frac{{\ln \left| x \right|}}{x}\) and \(h(x) = \frac{{\ln \left| x \right|}}{{\left| x \right|}}\) , where \(0 < x < {{\text{e}}^2}\) .
(i) Sketch the graph of \(y = g(x)\) .
(ii) Write down the range of \(g\) .
(iii) Find the values of \(x\) such that \(h(x) > g(x)\) .[6]
▶️Answer/Explanation
Markscheme
(i) \(f'(x) = \frac{{x\frac{1}{x} – \ln x}}{{{x^2}}}\) M1A1
\( = \frac{{1 – \ln x}}{{{x^2}}}\)
so \(f'(x) = 0\) when \(\ln x = 1\), i.e. \(x = {\text{e}}\) A1
(ii) \(f'(x) > 0\) when \(x < {\text{e}}\) and \(f'(x) < 0\) when \(x > {\text{e}}\) R1
hence local maximum AG
Note: Accept argument using correct second derivative.
(iii) \(y \leqslant \frac{1}{{\text{e}}}\) A1
[5 marks]
\(f”(x) = \frac{{{x^2}\frac{{ – 1}}{x} – \left( {1 – \ln x} \right)2x}}{{{x^4}}}\) M1
\( = \frac{{ – x – 2x + 2x\ln x}}{{{x^4}}}\)
\( = \frac{{ – 3 + 2\ln x}}{{{x^3}}}\) A1
Note: May be seen in part (a).
\(f”(x) = 0\) (M1)
\({ – 3 + 2\ln x = 0}\)
\(x = {{\text{e}}^{\frac{3}{2}}}\)
since \(f”(x) < 0\) when \(x < {{\text{e}}^{\frac{3}{2}}}\) and \(f”(x) > 0\) when \(x > {{\text{e}}^{\frac{3}{2}}}\) R1
then point of inflexion \(\left( {{{\text{e}}^{\frac{3}{2}}},\frac{3}{{2{{\text{e}}^{\frac{3}{2}}}}}} \right)\) A1
[5 marks]
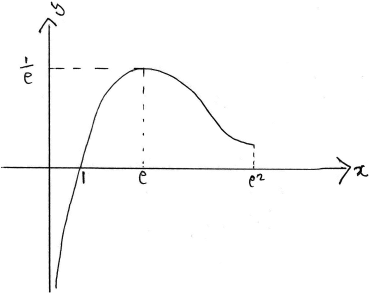A1A1A1
Note: Award A1 for the maximum and intercept, A1 for a vertical asymptote and A1 for shape (including turning concave up).
[3 marks]
(i)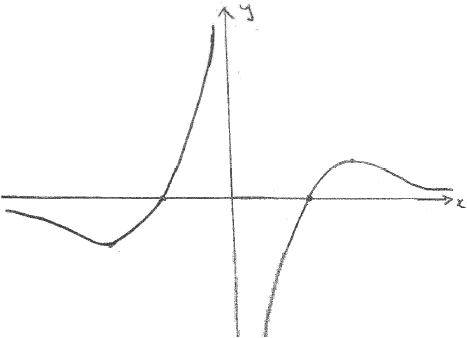
A1A1
Note: Award A1 for each correct branch.
(ii) all real values A1
(iii)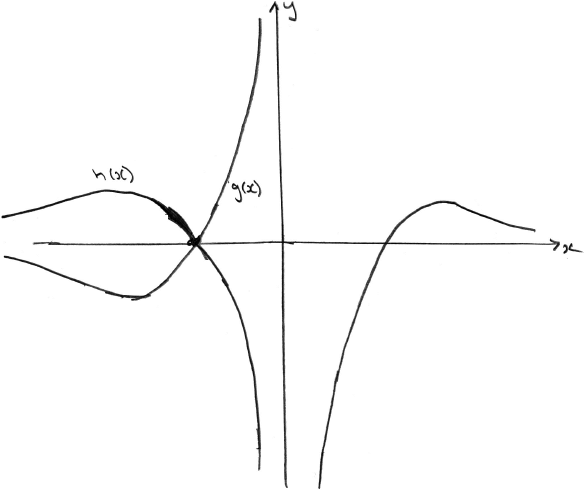
(M1)(A1)
Note: Award (M1)(A1) for sketching the graph of h, ignoring any graph of g.
\( – {{\text{e}}^2} < x < – 1\) (accept \(x < – 1\) ) A1
[6 marks]
Examiners report
Most candidates attempted parts (a), (b) and (c) and scored well, although many did not gain the reasoning marks for the justification of the existence of local maximum and inflexion point. The graph sketching was poorly done. A wide selection of range shapes were seen, in some cases showing little understanding of the relation between the derivatives of the function and its graph and difficulties with transformation of graphs. In some cases candidates sketched graphs consistent with their previous calculations but failed to label them properly.
Most candidates attempted parts (a), (b) and (c) and scored well, although many did not gain the reasoning marks for the justification of the existence of local maximum and inflexion point. The graph sketching was poorly done. A wide selection of range shapes were seen, in some cases showing little understanding of the relation between the derivatives of the function and its graph and difficulties with transformation of graphs. In some cases candidates sketched graphs consistent with their previous calculations but failed to label them properly.
Most candidates attempted parts (a), (b) and (c) and scored well, although many did not gain the reasoning marks for the justification of the existence of local maximum and inflexion point. The graph sketching was poorly done. A wide selection of range shapes were seen, in some cases showing little understanding of the relation between the derivatives of the function and its graph and difficulties with transformation of graphs. In some cases candidates sketched graphs consistent with their previous calculations but failed to label them properly.
Most candidates attempted parts (a), (b) and (c) and scored well, although many did not gain the reasoning marks for the justification of the existence of local maximum and inflexion point. The graph sketching was poorly done. A wide selection of range shapes were seen, in some cases showing little understanding of the relation between the derivatives of the function and its graph and difficulties with transformation of graphs. In some cases candidates sketched graphs consistent with their previous calculations but failed to label them properly.
Question
The diagram below shows a circular lake with centre O, diameter AB and radius 2 km.
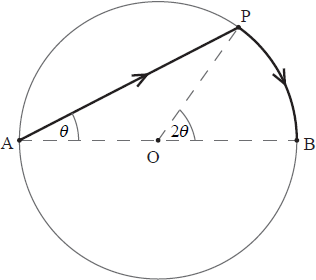
Jorg needs to get from A to B as quickly as possible. He considers rowing to point P and then walking to point B. He can row at \(3{\text{ km}}\,{{\text{h}}^{ – 1}}\) and walk at \(6{\text{ km}}\,{{\text{h}}^{ – 1}}\). Let \({\rm{P\hat AB}} = \theta \) radians, and t be the time in hours taken by Jorg to travel from A to B.
a.Show that \(t = \frac{2}{3}(2\cos \theta + \theta )\).[3]
b.Find the value of \(\theta \) for which \(\frac{{{\text{d}}t}}{{{\text{d}}\theta }} = 0\).[2]
c.What route should Jorg take to travel from A to B in the least amount of time?
Give reasons for your answer.[3]
▶️Answer/Explanation
Markscheme
angle APB is a right angle
\( \Rightarrow \cos \theta = \frac{{{\text{AP}}}}{4} \Rightarrow {\text{AP}} = 4\cos \theta \) A1
Note: Allow correct use of cosine rule.
\({\text{arc PB}} = 2 \times 2\theta = 4\theta \) A1
\(t = \frac{{{\text{AP}}}}{3} + \frac{{{\text{PB}}}}{6}\) M1
Note: Allow use of their AP and their PB for the M1.
\( \Rightarrow t = \frac{{4\cos \theta }}{3} + \frac{{4\theta }}{6} = \frac{{4\cos \theta }}{3} + \frac{{2\theta }}{3} = \frac{2}{3}(2\cos \theta + \theta )\) AG
[3 marks]
\(\frac{{{\text{d}}t}}{{{\text{d}}\theta }} = \frac{2}{3}( – 2\sin \theta + 1)\) A1
\(\frac{2}{3}( – 2\sin \theta + 1) = 0 \Rightarrow \sin \theta = \frac{1}{2} \Rightarrow \theta = \frac{\pi }{6}\) (or 30 degrees) A1
[2 marks]
\(\frac{{{{\text{d}}^2}t}}{{{\text{d}}{\theta ^2}}} = – \frac{4}{3}\cos \theta < 0\,\,\,\,\left( {{\text{at }}\theta = \frac{\pi }{6}} \right)\) M1
\( \Rightarrow t\) is maximized at \(\theta = \frac{\pi }{6}\) R1
time needed to walk along arc AB is \(\frac{{2\pi }}{6}{\text{ (}} \approx {\text{1 hour)}}\)
time needed to row from A to B is \(\frac{4}{3}{\text{ (}} \approx {\text{1.33 hour)}}\)
hence, time is minimized in walking from A to B R1
[3 marks]
Examiners report
The fairly easy trigonometry challenged a large number of candidates.
Part (b) was very well done.
Satisfactory answers were very rarely seen for (c). Very few candidates realised that a minimum can occur at the beginning or end of an interval.