Question
Five pipes labelled, “6 metres in length”, were delivered to a building site. The contractor measured each pipe to check its length (in metres) and recorded the following;
5.96, 5.95, 6.02, 5.95, 5.99.
(i) Find the mean of the contractor’s measurements.
(ii) Calculate the percentage error between the mean and the stated, approximate length of 6 metres.[3]
Calculate \(\sqrt {{{3.87}^5} – {{8.73}^{ – 0.5}}} \), giving your answer
(i) correct to the nearest integer,
(ii) in the form \(a \times 10^k\), where 1 ≤ a < 10, \(k \in {\mathbb{Z}}\) .[3]
Answer/Explanation
Markscheme
(i) Mean = (5.96 + 5.95 + 6.02 + 5.95 + 5.99) / 5 = 5.974 (5.97) (A1)
(ii) \({\text{% error}} = \frac{{error}}{{actualvalue}} \times 100\% \)
\( = \frac{{6 – 5.974}}{{5.974}} \times 100\% = 0.435\% \) (M1)(A1)(ft)
(M1) for correctly substituted formula.
Allow 0.503% as follow through from 5.97
Note: An answer of 0.433% is incorrect. (C3)[3 marks]
number is 29.45728613
(i) Nearest integer = 29 (A1)
(ii) Standard form = 2.95 × 101 (accept 2.9 × 101) (A1)(ft)(A1)
Award (A1) for each correct term
Award (A1)(A0) for 2.95 × 10 (C3)[3 marks]
Question
Calculate \(\frac{{77.2 \times {3^3}}}{{3.60 \times {2^2}}}\).[1]
Express your answer to part (a) in the form \(a \times 10^k\), where \(1 \leqslant a < 10\) and \(k \in {\mathbb{Z}}\).[2]
Juan estimates the length of a carpet to be 12 metres and the width to be 8 metres. He then estimates the area of the carpet.
(i) Write down his estimated area of the carpet.
When the carpet is accurately measured it is found to have an area of 90 square metres.
(ii) Calculate the percentage error made by Juan.[3]
Answer/Explanation
Markscheme
\(144.75\left( { = \frac{{579}}{4}} \right)\) (A1)
accept 145 (C1)[1 mark]
\(1.4475 \times 10^2\) (A1)(ft)(A1)(ft)
accept \(1.45 \times 10^2\) (C2)[2 marks]
Unit penalty (UP) is applicable in question part (c)(i) only.
(UP) (i) Area = 96 m2 (A1)
(ii) \(\% {\text{ error}} = \frac{{(96 – 90)}}{{90}} \times 100\) (M1)
\( = \frac{{6 \times 100}}{{90}}\)
\(\frac{{20}}{3}\% \) or 6.67 % (A1)(ft) (C3)[3 marks]
Question
The following diagram shows a rectangle with sides of length 9.5 ×102 m and 1.6 ×103 m.
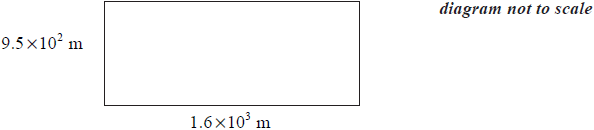
Write down the area of the rectangle in the form a × 10k, where 1 ≤ a < 10, k ∈ \(\mathbb{Z}\).[3]
Helen’s estimate of the area of the rectangle is \(1\,600\,000{\text{ }}{{\text{m}}^2}\).
Find the percentage error in Helen’s estimate.[3]
Answer/Explanation
Markscheme
UP applies in part (a).
\(9.5 \times 10^2 \times 1.6 \times 10^3\) (M1)
(UP) \( = 1.52 \times {10^6}{\text{ }}{{\text{m}}^2}\) (A1)(A1) (C3)
Notes: Award (M1) for multiplication of the two numbers.
Award (A1) for \(1.52\), (A1) for \(10^6\).[3 marks]
\(\frac{{1600000 – 1520000}}{{1520000}} \times 100\) (M1)(A1)(ft)
Note: Award (M1) for substitution in formula, (A1)(ft) for their correct substitution.
= 5.26 % (percent sign not required). (A1)(ft) (C3)
Note: Accept positive or negative answer.[3 marks]
Question
Consider c = 5200 and d = 0.0000037.
Write down the value of r = c × d.[1]
Write down your value of r in the form a × 10k, where 1 ≤ a < 10 and \(k \in \mathbb{Z}\).[2]
Consider the following statements about c, d and r. Only three of these statements are true.
Circle the true statements.
 [3]
[3]
Answer/Explanation
Markscheme
r = 0.01924 (A1) (C1)
Note: Accept 0.0192 and 0.019[1 mark]
r = 1.924 × 10−2 (A1)(ft)(A1)(ft) (C2)
Notes: Award (A1) for 1.924, (A1) for 10−2. Accept 1.92 and 1.9. Follow through from their part (a).[2 marks]
(A1)(A1)(A1) (C3)
Notes: Award (A1) for each true statement circled. Do not follow through from part (a). Award (A1)(A1)(A0) if 1 extra term seen. Award (A1)(A0)(A0) if 2 extra terms seen. Award (A0)(A0)(A0) if all terms circled. Accept other indications of the correct statements i.e. highlighted or ticks.[3 marks]
