Question
Find the set of values of x for which \(\left| {0.1{x^2} – 2x + 3} \right| < {\log _{10}}x\) .
▶️Answer/Explanation
Markscheme
Attempting to solve \(\left| {0.1{x^2} – 2x + 3} \right| = {\log _{10}}x\) numerically or graphically. (M1)
x = 1.52, 1.79 (A1)(A1)
x = 17.6, 19.1 (A1)
\((1.52 < x < 1.79) \cup (17.6 < x < 19.1)\) A1A1 N2
[6 marks]
Examiners report
This question was generally not well done. A number of candidates attempted an ‘ill-fated’ algebraic approach. Most candidates who used their GDC were able to correctly locate one inequality. The few successful candidates were able to employ a suitable window or suitable window(s) to correctly locate both inequalities.
Question
(a) Sketch the curve \(y = \left| {\ln x} \right| – \left| {\cos x} \right| – 0.1\) , \(0 < x < 4\) showing clearly the coordinates of the points of intersection with the x-axis and the coordinates of any local maxima and minima.
(b) Find the values of x for which \(\left| {\ln x} \right| > \left| {\cos x} \right| + 0.1\), \(0 < x < 4\) .
▶️Answer/Explanation
Markscheme
(a)
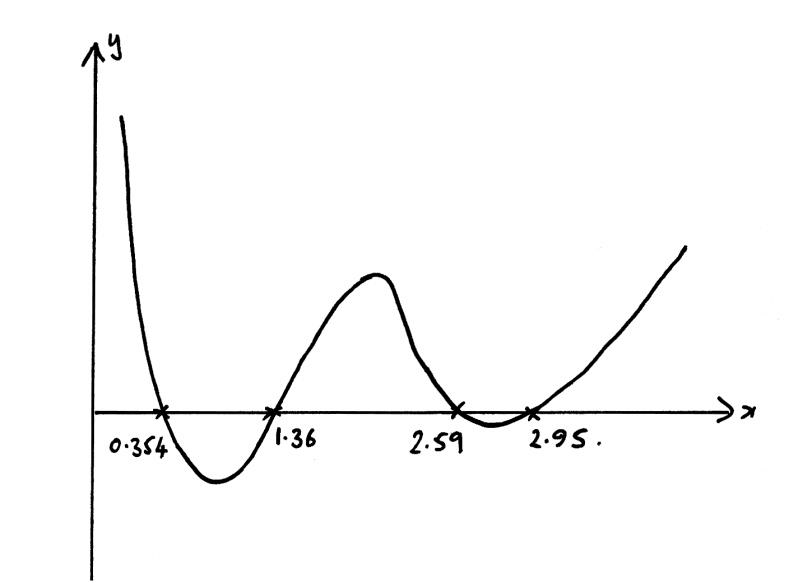A1
Note: Award A1 for shape.
x-intercepts 0.354, 1.36, 2.59, 2.95 A2
Note: Award A1 for three correct, A0 otherwise.
maximum = (1.57, 0.352) = \(\left( {\frac{\pi }{2},0.352} \right)\) A1
minimum = (1, – 0.640) and (2.77, – 0.0129) A1
(b) \(0 < x < 0.354,{\text{ }}1.36 < x < 2.59,{\text{ }}2.95 < x < 4\) A2
Note: Award A1 if two correct regions given.
[7 marks]
Examiners report
Solutions to this question were extremely disappointing with many candidates doing the sketch in degree mode instead of radian mode. The two adjacent intercepts at 2.59 and 2.95 were often missed due to an unsatisfactory window. Some sketches were so small that a magnifying glass was required to read some of the numbers; candidates would be well advised to draw sketches large enough to be easily read.
Question
Let \(f(x) = \frac{{1 – x}}{{1 + x}}\) and \(g(x) = \sqrt {x + 1} \), \(x > – 1\).
Find the set of values of \(x\) for which \(f'(x) \leqslant f(x) \leqslant g(x)\) .
▶️Answer/Explanation
Markscheme
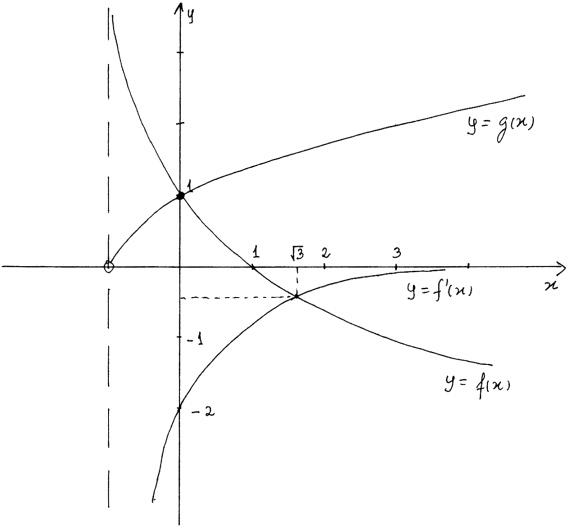
\(f'(x) = \frac{{ – 2}}{{{{\left( {1 + x} \right)}^2}}}\) M1A1
Note: Alternatively, award M1A1 for correct sketch of the derivative.
find at least one point of intersection of graphs (M1)
\(y = f(x)\) and \(y = f'(x)\) for \(x = \sqrt 3 \) or \(1.73\) (A1)
\(y = f(x)\) and \(y = g(x)\) for \(x = 0\) (A1)
forming inequality \(0 \leqslant x \leqslant \sqrt 3 \) (or \(0 \leqslant x \leqslant 1.73\)) A1A1 N4
Note: Award A1 for correct limits and A1 for correct inequalities.
[7 marks]
Examiners report
Most students were able to find the derived function correctly, although attempts to solve the inequality algebraically were often unsuccessful. This was a question where students prepared in good use of GDC were able to easily obtain good marks.
Question
Let \(f(x) = \frac{{4 – {x^2}}}{{4 – \sqrt x }}\).
(a) State the largest possible domain for f.
(b) Solve the inequality \(f(x) \geqslant 1\).
▶️Answer/Explanation
Markscheme
(a) \(x \geqslant 0\) and \(x \ne 16\) A1A1
(b)
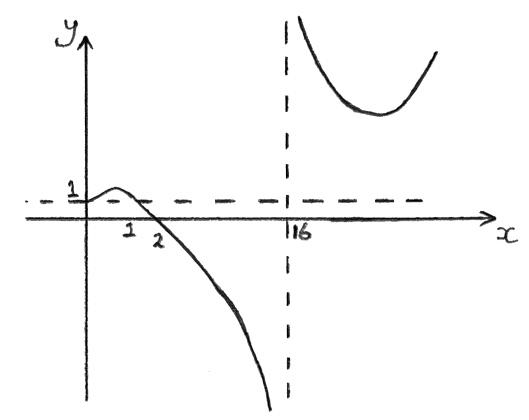graph not to scale
finding crossing points (M1)
e.g. \(4 – {x^2} = 4 – \sqrt x \)
x = 0 or x = 1 (A1)
\(0 \leqslant x \leqslant 1\) or \(x > 16\) A1A1
Note: Award M1A1A1A0 for solving the inequality only for the case \(x < 16\).
[6 marks]
Examiners report
Most students were able to obtain partial marks, but there were very few completely correct answers.