Home / Concept of a vector AA HL Paper 3

IB Mathematics AHL 3.12 Concept of a vector AA HL Paper 3- Exam Style Questions

IB DP Math AA HL Papers 3 -All Topics

Question

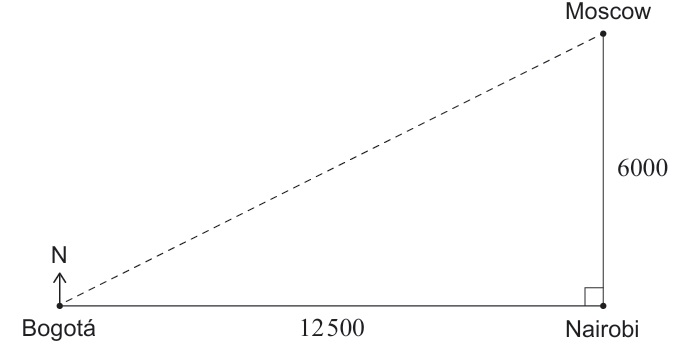
This problem evaluates the spatial relationships between three global cities by comparing calculations performed on a \(2\)-D Euclidean plane versus a \(3\)-D spherical model.

In the Euclidean (flat) model, the locations are defined as follows:

  • Nairobi is situated \(6000\) km directly south of Moscow.
  • Bogotá is situated \(12\,500\) km directly west of Nairobi.
 
 
(a) (i) Calculate the direct distance between Bogotá and Moscow using this \(2\)-D representation.
(a) (ii) Determine the bearing of Moscow from Bogotá in degrees.
For the following sections, the Earth is represented as a sphere with a radius of \(6000\) km. A Cartesian coordinate system \((x, y, z)\) is established with the origin at the center of the Earth. The North Pole \(P\) is located on the positive \(z\)-axis, and Nairobi \(N\) is located on the equator along the positive \(y\)-axis.
 
 
The position vectors are given by: \( \mathbf{p} = \overrightarrow{OP} = \begin{pmatrix}0\\0\\6\end{pmatrix} \) and \( \mathbf{n} = \overrightarrow{ON} = \begin{pmatrix}0\\6\\0\end{pmatrix}. \)
(b) (i) Find the angle between vectors \(\mathbf{p}\) and \(\mathbf{n}\) using the scalar product.
(b) (ii) Show that the great-circle distance (arc length) between \(P\) and \(N\) is exactly \(3000\pi\) km.
A third location \(A\) on the equator has the position vector \(\mathbf{a} = \begin{pmatrix}6\\0\\0\end{pmatrix}\). Points \(P, N,\) and \(A\) define a spherical triangle connected by arcs of great circles. The interior angle at vertex \(A\) is defined as the angle between the normal vectors \(\mathbf{a} \times \mathbf{p}\) and \(\mathbf{a} \times \mathbf{n}\).
 
 
(c) (i) Compute the vector product \(\mathbf{a} \times \mathbf{p}\).
(c) (ii) Verify that the interior angle at vertex \(A\) in this triangle is \(90^\circ\).
Moscow \(M\) is assigned the position vector \( \mathbf{m} = \overrightarrow{OM} = \begin{pmatrix}0\\6\cos\theta\\6\sin\theta\end{pmatrix}. \) The shortest surface distance between Moscow and Nairobi is measured to be \(6000\) km.
 
 
 
(d) Demonstrate that \(\theta \approx 57.3^\circ\) to three significant figures.
Bogotá \(B\) is located west of Nairobi with position vector \( \mathbf{b} = \overrightarrow{OB} = \begin{pmatrix}6\sin120^\circ\\6\cos120^\circ\\0\end{pmatrix}. \)
(e) Calculate the shortest surface distance between Bogotá and Moscow on this spherical model.
The spherical bearing from \(B\) to \(M\) is the angle at vertex \(B\) in the spherical triangle formed by \(B, M,\) and \(P\). Given that \( \mathbf{b} \times \mathbf{p} = \begin{pmatrix}36\cos120^\circ\\ -36\sin120^\circ\\ 0\end{pmatrix} \):
(f) Determine the bearing from Bogotá to Moscow using the vector method established in part (c).

Most‑appropriate topic codes (IB Mathematics AA AHL):

• AHL 3.12: Vector representation in three dimensions; magnitude of a vector; unit vectors; position vectors.
• AHL 3.13: Scalar product of two vectors; properties of the scalar product; angle between two vectors.
• AHL 3.16: Vector product of two vectors; properties of the vector product; geometric interpretation.
▶️ Answer/Explanation

(a) (i)
Distance = \(\sqrt{6000^2 + 12500^2}\)
Distance = \(\sqrt{36,000,000 + 156,250,000} = \sqrt{192,250,000}\)
Distance \(\approx 13865.4\) km
Answer: 13900 km (to 3 significant figures).

(a) (ii)
Let Moscow be at (0, 6000) and Nairobi at (0, 0). Bogotá is at (-12500, 0).
The angle \(\alpha\) from the North-South line satisfies \(\tan \alpha = \frac{12500}{6000}\).
\(\alpha = \arctan(2.0833…) \approx 64.36^\circ\).
Bearing = 064.4°.

(b) (i)
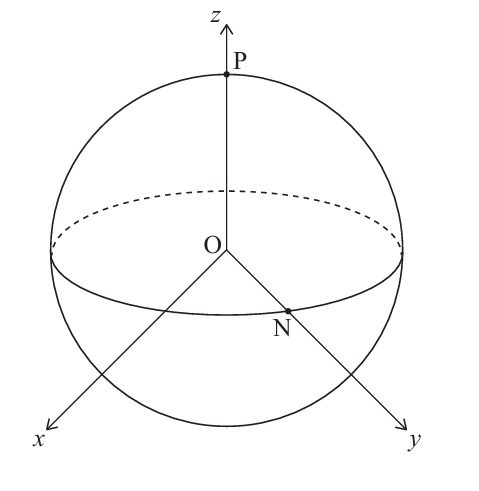
Using \(\mathbf{p} \cdot \mathbf{n} = |\mathbf{p}| |\mathbf{n}| \cos \theta\):
\(\begin{pmatrix} 0 \\ 0 \\ 6 \end{pmatrix} \cdot \begin{pmatrix} 0 \\ 6 \\ 0 \end{pmatrix} = (0)(0) + (0)(6) + (6)(0) = 0\).
\(36 \cos \theta = 0 \implies \cos \theta = 0\).
Angle = 90° (or \(\pi/2\) radians).

(b) (ii)
Distance = \(r \theta\).
Distance = \(6000 \times \frac{\pi}{2} = 3000\pi\) km.

(c) (i)
\(\mathbf{a} \times \mathbf{p} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 6 & 0 & 0 \\ 0 & 0 & 6 \end{vmatrix} = \mathbf{i}(0-0) – \mathbf{j}(36-0) + \mathbf{k}(0-0) = \begin{pmatrix} 0 \\ -36 \\ 0 \end{pmatrix}\).

(c) (ii)
\(\mathbf{a} \times \mathbf{n} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 6 & 0 & 0 \\ 0 & 6 & 0 \end{vmatrix} = \mathbf{i}(0-0) – \mathbf{j}(0-0) + \mathbf{k}(36-0) = \begin{pmatrix} 0 \\ 0 \\ 36 \end{pmatrix}\).
Let \(\phi\) be the angle at vertex A.
\(\cos \phi = \frac{(\mathbf{a} \times \mathbf{p}) \cdot (\mathbf{a} \times \mathbf{n})}{|\mathbf{a} \times \mathbf{p}| |\mathbf{a} \times \mathbf{n}|} = \frac{0 + 0 + 0}{36 \times 36} = 0\).
\(\phi = 90^\circ\).

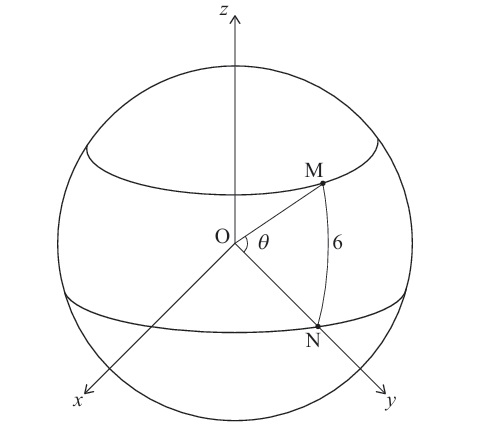
(d)
Arc length MN = 6000 km.
Angle between \(\mathbf{m}\) and \(\mathbf{n}\) is \(\theta_{MN} = \frac{\text{Arc}}{\text{Radius}} = \frac{6000}{6000} = 1\) radian.
Using \(\mathbf{m} \cdot \mathbf{n} = |\mathbf{m}| |\mathbf{n}| \cos \theta_{MN}\):
\(\begin{pmatrix} 0 \\ 6\cos\theta \\ 6\sin\theta \end{pmatrix} \cdot \begin{pmatrix} 0 \\ 6 \\ 0 \end{pmatrix} = 36\cos\theta_{MN}\).
\(36\cos\theta = 36\cos(1)\).
\(\theta = 1\) radian \(\approx 57.2958^\circ\).
\(\theta = 57.3^\circ\) (to 3 s.f.).

(e)
The angle \(\psi\) between \(\mathbf{b}\) and \(\mathbf{m}\) is found via \(\mathbf{b} \cdot \mathbf{m}\):
\(\mathbf{b} \cdot \mathbf{m} = (6\sin 120^\circ)(0) + (6\cos 120^\circ)(6\cos \theta) + (0)(6\sin \theta)\).
\(\mathbf{b} \cdot \mathbf{m} = 36(-\frac{1}{2})\cos(1) \approx -18(0.5403…) \approx -9.7254\).
\(\cos \psi = \frac{-9.7254}{36} \approx -0.27015\).
\(\psi = \arccos(-0.27015) \approx 1.844\) radians.
Distance = \(6000 \times 1.844 \approx 11064\) km.
Answer: 11100 km (to 3 s.f.).

(f)
Bearing is the angle between \(\mathbf{b} \times \mathbf{p}\) and \(\mathbf{b} \times \mathbf{m}\).
\(\mathbf{b} \times \mathbf{p} = \begin{pmatrix} -18 \\ -18\sqrt{3} \\ 0 \end{pmatrix}\).
\(\mathbf{b} \times \mathbf{m} = \begin{pmatrix} (6\cos 120^\circ)(6\sin\theta) – 0 \\ 0 – (6\sin 120^\circ)(6\sin\theta) \\ (6\sin 120^\circ)(6\cos\theta) – 0 \end{pmatrix} = \begin{pmatrix} -18\sin 1 \\ -18\sqrt{3}\sin 1 \\ 18\sqrt{3}\cos 1 \end{pmatrix}\).
Dot product \(= (-18)(-18\sin 1) + (-18\sqrt{3})(-18\sqrt{3}\sin 1) + 0 = 324\sin 1 + 972\sin 1 = 1296\sin 1 \approx 1090.5\).
\(|\mathbf{b} \times \mathbf{p}| = 36\).
\(|\mathbf{b} \times \mathbf{m}| = \sqrt{(-18\sin 1)^2 + (-18\sqrt{3}\sin 1)^2 + (18\sqrt{3}\cos 1)^2} \approx 34.66\).
\(\cos(\text{bearing}) = \frac{1090.5}{36 \times 34.66} \approx 0.874 \implies \text{Bearing} \approx 29.1^\circ\).
Answer: 029.1°.

More MAA HL Paper 3 Questions
Scroll to Top