Question
An infinite geometric series has first term u1 = a and second term u2 = \(\frac{1}{4}\)a2– 3a , where a > 0 .
Find the common ratio in terms of a . [2]
Find the values of a for which the sum to infinity of the series exists. [3]
Find the value of a when S∞ = 76. [3]
Answer/Explanation
Ans

Question
The first three terms of a geometric sequence are \(\ln {x^{16}}\), \(\ln {x^8}\), \(\ln {x^4}\), for \(x > 0\).
Find the common ratio.
Solve \(\sum\limits_{k = 1}^\infty {{2^{5 – k}}\ln x = 64} \).
Answer/Explanation
Markscheme
correct use \(\log {x^n} = n\log x\) A1
eg\(\,\,\,\,\,\)\(16\ln x\)
valid approach to find \(r\) (M1)
eg\(\,\,\,\,\,\)\(\frac{{{u_{n + 1}}}}{{{u_n}}},{\text{ }}\frac{{\ln {x^8}}}{{\ln {x^{16}}}},{\text{ }}\frac{{4\ln x}}{{8\ln x}},{\text{ }}\ln {x^4} = \ln {x^{16}} \times {r^2}\)
\(r = \frac{1}{2}\) A1 N2
[3 marks]
recognizing a sum (finite or infinite) (M1)
eg\(\,\,\,\,\,\)\({2^4}\ln x + {2^3}\ln x,{\text{ }}\frac{a}{{1 – r}},{\text{ }}{S_\infty },{\text{ }}16\ln x + \ldots \)
valid approach (seen anywhere) (M1)
eg\(\,\,\,\,\,\)recognizing GP is the same as part (a), using their \(r\) value from part (a), \(r = \frac{1}{2}\)
correct substitution into infinite sum (only if \(\left| r \right|\) is a constant and less than 1) A1
eg\(\,\,\,\,\,\)\(\frac{{{2^4}\ln x}}{{1 – \frac{1}{2}}},{\text{ }}\frac{{\ln {x^{16}}}}{{\frac{1}{2}}},{\text{ }}32\ln x\)
correct working (A1)
eg\(\,\,\,\,\,\)\(\ln x = 2\)
\(x = {{\text{e}}^2}\) A1 N3
[5 marks]
Question
The first three terms of a infinite geometric sequence are \(m – 1,{\text{ 6, }}m + 4\), where \(m \in \mathbb{Z}\).
Write down an expression for the common ratio, \(r\).
Hence, show that \(m\) satisfies the equation \({m^2} + 3m – 40 = 0\).
Find the two possible values of \(m\).
Find the possible values of \(r\).
The sequence has a finite sum.
State which value of \(r\) leads to this sum and justify your answer.
The sequence has a finite sum.
Calculate the sum of the sequence.
Answer/Explanation
Markscheme
correct expression for \(r\) A1 N1
eg \(r = \frac{6}{{m – 1}},{\text{ }}\frac{{m + 4}}{6}\)
[2 marks]
correct equation A1
eg \(\frac{6}{{m – 1}} = \frac{{m + 4}}{6},{\text{ }}\frac{6}{{m + 4}} = \frac{{m – 1}}{6}\)
correct working (A1)
eg \((m + 4)(m – 1) = 36\)
correct working A1
eg \({m^2} – m + 4m – 4 = 36,{\text{ }}{m^2} + 3m – 4 = 36\)
\({m^2} + 3m – 40 = 0\) AG N0
[2 marks]
valid attempt to solve (M1)
eg \((m + 8)(m – 5) = 0,{\text{ }}m = \frac{{ – 3 \pm \sqrt {9 + 4 \times 40} }}{2}\)
\(m = – 8,{\text{ }}m = 5\) A1A1 N3
[3 marks]
attempt to substitute any value of \(m\) to find \(r\) (M1)
eg \(\frac{6}{{ – 8 – 1}},{\text{ }}\frac{{5 + 4}}{6}\)
\(r = \frac{3}{2},{\text{ }}r = – \frac{2}{3}\) A1A1 N3
[3 marks]
\(r = – \frac{2}{3}\) (may be seen in justification) A1
valid reason R1 N0
eg \(\left| r \right| < 1,{\text{ }} – 1 < \frac{{ – 2}}{3} < 1\)
Notes: Award R1 for \(\left| r \right| < 1\) only if A1 awarded.
[2 marks]
finding the first term of the sequence which has \(\left| r \right| < 1\) (A1)
eg \( – 8 – 1,{\text{ }}6 \div \frac{{ – 2}}{3}\)
\({u_1} = – 9\) (may be seen in formula) (A1)
correct substitution of \({u_1}\) and their \(r\) into \(\frac{{{u_1}}}{{1 – r}}\), as long as \(\left| r \right| < 1\) A1
eg \({S_\infty } = \frac{{ – 9}}{{1 – \left( { – \frac{2}{3}} \right)}},{\text{ }}\frac{{ – 9}}{{\frac{5}{3}}}\)
\({S_\infty } = – \frac{{27}}{5}{\text{ }}( = – 5.4)\) A1 N3
[4 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
Question
The following diagram shows [AB], with length 2 cm. The line is divided into an infinite number of line segments. The diagram shows the first three segments.

The length of the line segments are \(p{\text{ cm}},{\text{ }}{p^2}{\text{ cm}},{\text{ }}{p^3}{\text{ cm}},{\text{ }} \ldots \), where \(0 < p < 1\).
Show that \(p = \frac{2}{3}\).
The following diagram shows [CD], with length \(b{\text{ cm}}\), where \(b > 1\). Squares with side lengths \(k{\text{ cm}},{\text{ }}{k^2}{\text{ cm}},{\text{ }}{k^3}{\text{ cm}},{\text{ }} \ldots \), where \(0 < k < 1\), are drawn along [CD]. This process is carried on indefinitely. The diagram shows the first three squares.
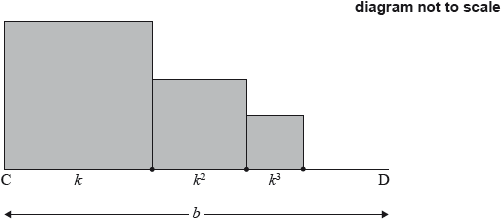
The total sum of the areas of all the squares is \(\frac{9}{{16}}\). Find the value of \(b\).
Answer/Explanation
Markscheme
infinite sum of segments is 2 (seen anywhere) (A1)
eg\(\,\,\,\,\,\)\(p + {p^2} + {p^3} + \ldots = 2,{\text{ }}\frac{{{u_1}}}{{1 – r}} = 2\)
recognizing GP (M1)
eg\(\,\,\,\,\,\)ratio is \(p,{\text{ }}\frac{{{u_1}}}{{1 – r}},{\text{ }}{u_n} = {u_1} \times {r^{n – 1}},{\text{ }}\frac{{{u_1}({r^n} – 1)}}{{r – 1}}\)
correct substitution into \({S_\infty }\) formula (may be seen in equation) A1
eg\(\,\,\,\,\,\)\(\frac{p}{{1 – p}}\)
correct equation (A1)
eg\(\,\,\,\,\,\)\(\frac{p}{{1 – p}} = 2,{\text{ }}p = 2 – 2p\)
correct working leading to answer A1
eg\(\,\,\,\,\,\)\(3p = 2,{\text{ }}2 – 3p = 0\)
\(p = \frac{2}{3}{\text{ (cm)}}\) AG N0
[5 marks]
recognizing infinite geometric series with squares (M1)
eg\(\,\,\,\,\,\)\({k^2} + {k^4} + {k^6} + \ldots ,{\text{ }}\frac{{{k^2}}}{{1 – {k^2}}}\)
correct substitution into \({S_\infty } = \frac{9}{{16}}\) (must substitute into formula) (A2)
eg\(\,\,\,\,\,\)\(\frac{{{k^2}}}{{1 – {k^2}}} = \frac{9}{{16}}\)
correct working (A1)
eg\(\,\,\,\,\,\)\(16{k^2} = 9 – 9{k^2},{\text{ }}25{k^2} = 9,{\text{ }}{k^2} = \frac{9}{{25}}\)
\(k = \frac{3}{5}\) (seen anywhere) A1
valid approach with segments and CD (may be seen earlier) (M1)
eg\(\,\,\,\,\,\)\(r = k,{\text{ }}{S_\infty } = b\)
correct expression for \(b\) in terms of \(k\) (may be seen earlier) (A1)
eg\(\,\,\,\,\,\)\(b = \frac{k}{{1 – k}},{\text{ }}b = \sum\limits_{n = 1}^\infty {{k^n},{\text{ }}b = k + {k^2} + {k^3} + \ldots } \)
substituting their value of \(k\) into their formula for \(b\) (M1)
eg\(\,\,\,\,\,\)\(\frac{{\frac{3}{5}}}{{1 – \frac{3}{5}}},{\text{ }}\frac{{\left( {\frac{3}{5}} \right)}}{{\left( {\frac{2}{5}} \right)}}\)
\(b = \frac{3}{2}\) A1 N3
[9 marks]
