IBDP Maths SL 2.1 equation of a straight line AA HL Paper 2- Exam Style Questions- New Syllabus
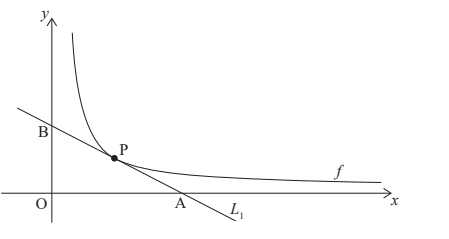
The following diagram shows part of the graph of \( f(x) = \frac{k}{x} \), for \( x > 0 \), \( k > 0 \).
Let \( P \), \( \left(p, \frac{k}{p}\right) \) be any point on the graph of \( f \). Line \( L_1 \) is the tangent to the graph of \( f \) at \( P \).
(a)
(i) Find \( f'(p) \) in terms of \( k \) and \( p \). [2 marks]
(ii) Show that the equation of \( L_1 \) is \( kx + p^2 y – 2pk = 0 \). [4 marks]
Line \( L_1 \) intersects the \( x \)-axis at point \( A(2p, 0) \) and the \( y \)-axis at point \( B \).
(b) Find the area of triangle \( AOB \) in terms of \( k \). [5 marks]
The graph of \( f \) is translated by \( \begin{pmatrix} 4 \\ 3 \end{pmatrix} \) to give the graph of \( g \).
In the following diagram:
- point \( Q \) lies on the graph of \( g \)
- points \( C \), \( D \), and \( E \) lie on the vertical asymptote of \( g \)
- points \( D \) and \( F \) lie on the horizontal asymptote of \( g \)
- point \( G \) lies on the \( x \)-axis such that \( FG \) is parallel to \( DC \).
Line \( L_2 \) is the tangent to the graph of \( g \) at \( Q \), and passes through \( E \) and \( F \).
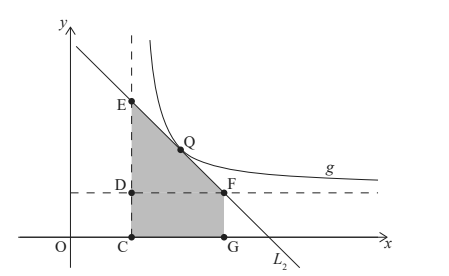
(c) Given that triangle \( EDF \) and rectangle \( CDFG \) have equal areas, find the gradient of \( L_2 \) in terms of \( p \). [6 marks]
▶️ Answer/Explanation
(a)
(i)
\( f'(x) = -k x^{-2} \)
\( f'(p) = -k p^{-2} = -\frac{k}{p^2} \). A1
[2 marks]
(ii)
Attempt to use point and gradient to find equation of \( L_1 \). M1
e.g., \( y – \frac{k}{p} = -k p^{-2} (x – p) \), or \( \frac{k}{p} = -\frac{k}{p^2} p + b \)
Correct working leading to answer:
e.g., \( p^2 y – k p = -k x + k p \), or \( y – \frac{k}{p} = -\frac{k}{p^2} x + \frac{2k}{p} \). M1
\( k x + p^2 y – 2p k = 0 \). A1
[4 marks]
(b)
METHOD 1
Area of a triangle. M1
Recognizing \( x = 0 \) at \( B \). M1
Correct working to find \( y \)-coordinate of \( B \):
\( p^2 y – 2p k = 0 \implies y = \frac{2k}{p} \) (may be seen in area formula). A1
Correct substitution to find area of triangle:
e.g., \( \frac{1}{2} (2p) \left( \frac{2k}{p} \right) \), or \( p \times \frac{2k}{p} \). M1
Area of triangle \( AOB = 2k \). A1
METHOD 2
Integration, recognizing to integrate \( L_1 \) between 0 and \( 2p \). M1
e.g., \( \int_0^{2p} L_1 \, dx \), or \( \int_0^{2p} \left( -\frac{k}{p^2} x + \frac{2k}{p} \right) \, dx \)
Correct integration of both terms:
e.g., \( -\frac{k x^2}{2 p^2} + \frac{2k x}{p} \). M1
Substituting limits into integrated function and subtracting:
e.g., \( \left( -\frac{k (2p)^2}{2 p^2} + \frac{2k (2p)}{p} \right) – (0) \), or \( -\frac{4k p^2}{2 p^2} + \frac{4k p}{p} \). M1
Correct working: e.g., \( -2k + 4k \). A1
Area of triangle \( AOB = 2k \). A1
[5 marks]
(c)
Recognizing use of transformation. M1
e.g., area of triangle \( AOB = \) area of triangle \( DEF \), \( g(x) = \frac{k}{x – 4} + 3 \), gradient of \( L_2 = \) gradient of \( L_1 \), \( D(4, 3) \), \( 2p + 4 \), one correct shift.
Correct working:
e.g., area of triangle \( DEF = 2k \), \( CD = 3 \), \( DF = 2p \), \( CG = 2p \), \( E \left( 4, \frac{2k}{p} + 3 \right) \). A1
Area of rectangle \( CDFG = 2k \). A1
Valid approach:
e.g., \( \frac{ED \times DF}{2} = CD \times DF \), or \( 2p \cdot 3 = 2k \), or \( ED = CD \), or \( \int_4^{2p + 4} L_2 \, dx = 4k \). M1
Correct working:
e.g., \( ED = 6 \), \( E(4, 9) \), \( k = 3p \), gradient = \( \frac{3 – \left( \frac{2k}{p} + 3 \right)}{(2p + 4) – 4} \), or \( \frac{-6}{\frac{2k}{3}} \), or \( -\frac{9}{k} \). M1
e.g., \( \frac{-6}{2p} \), or \( \frac{9 – 3}{(2p + 4) – 4} \), or \( -\frac{3p}{p^2} \), or \( \frac{3 – \left( \frac{2(3p)}{p} + 3 \right)}{(2p + 4) – 4} \), or \( -\frac{9}{3p} \). A1
Gradient of \( L_2 \) is \( -\frac{3}{p} = -3 p^{-1} \). A1
[6 marks]
