Question
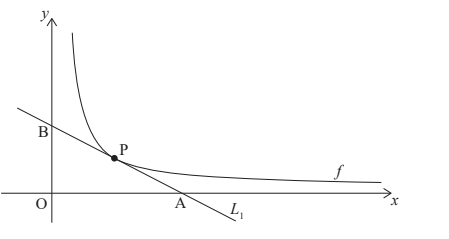
The following diagram shows part of the graph of f (x) = \(\frac{k}{x}\), for x > 0, k > 0.
Let P, \(p(p,\frac{k}{p})\) be any point on the graph of f . Line L1 is the tangent to the graph of f at P.
 x
x(i) Find f ′( p) in terms of k and p .
(ii) Show that the equation of L1 is kx + p2y – 2pk = 0. [4]
Line L1 intersects the x-axis at point A(2p , 0) and the y-axis at point B.
Find the area of triangle AOB in terms of k . [5]
The graph of f is translated by \((_{3}^{4})\) to give the graph of g .
In the following diagram:
point Q lies on the graph of g
points C, D and E lie on the vertical asymptote of g
points D and F lie on the horizontal asymptote of g
point G lies on the x-axis such that FG is parallel to DC.
Line L2 is the tangent to the graph of g at Q, and passes through E and F.
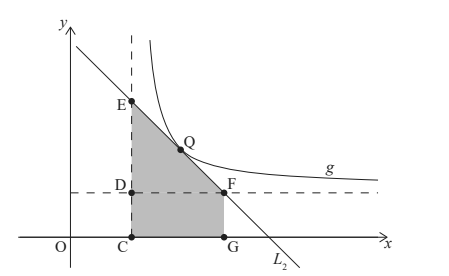
Given that triangle EDF and rectangle CDFG have equal areas, find the gradient of L2 in terms of p . [6]
▶️Answer/Explanation
Ans:
(a)
(i)
f'(x)= \(-kx^{-2}\)
\(f'(p)= -kp^{-2} (= – \frac{k}{p^{2}})\)
(ii)
attempt to use point and gradient to find equation of L1
eg y- \(\frac{k}{p}= – kp^{-2}(x-p), \frac{k}{p}= -\frac{k}{p^{2}}(p)\)+b
correct working leading to answer
eg \(p^{2}y-kp = -kx+kp, y -\frac{k}{p} =-\frac{k}{p^{2}}x+ \frac{k}{p}y=-\frac{k}{p^{2}}x+\frac{2k}{p}\)
\(kx+p^{2}\)y-2pk=0
(b)
METHOD 1
– area of a triangle
recognizing x = 0 at B
correct working to find y -coordinate of B
\(p^{2}y-2pk=0\)
y -coordinate of B at y = \(\frac{2k}{p}\)(may be seen in area formula)
correct substitution to find area of triangle
eg \(\frac{1}{2}(2p)(\frac{2k}{p}),p \times (\frac{2k}{p})\)
area of triangle AOB = 2k
METHOD 2 –
integration recognizing to integrate L1 between 0 and 2p
eg \(\int_{0}^{2p}L_{1}dx, \int_{0}^{2p} – \frac{k}{p^{2}}x+ \frac{2k}{p}\)
correct integration of both terms
eg \(-\frac{kx^{2}}{2p^{2}}+\frac{2kx}{p},-\frac{k}{2p^{2}}x^{2}+\frac{2k}{p}x+c\),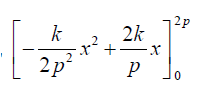
substituting limits into their integrated function and subtracting (in either order)
eg \(-\frac{k(2p^{2})}{2p^{2}}+\frac{2k(2p)}{p}-(0),-\frac{4kp^{2}}{2p^{2}}+\frac{4kp}{p}\)
correct working
eg -2k+4k
area of triangle AOB = 2K
(c)
recognizing use of transformation
eg area of triangle AOB = area of triangle DEF, g(x)= \(\frac{k}{x-4}+3\)
gradient of \(L_{2}\)= gradient of \(L_{1} ,D(4,3)\),2p+4, one correct shift
correct working
eg area of tringle DEF = 2k, CD = 3, DF= 2P, CG= 2P, E(4,\(\frac{2k}{p}+3)\)
area of rectangle CDFG = 2k
valid approach
eg \(\frac{ED\times DF}{2}\)=\(CD\times DF 2P.3= 2K ,ED =CD \), \(\int_{4}^{2P+4}L_{2}\)dx= 4k
correct working
eg ED = 6, E(4,9),K= 3p, gradient = \(\frac{3-(\frac{2k}{p}+3)}{(2p+4)-4},\frac{-6}{\frac{2k}{3}},-\frac{9}{k}\)
eg \(\frac{-6}{2p},\frac{9-3}{4-(2p+4)},-\frac{3p}{p^2},\frac{3-(\frac{2(3p)}{p}+3)}{(2p+4)-4}, – \frac{9}{3p}\)
gradient of
\(L_{2}is – \frac{3}{p}(=-3p^{-1})\)
Question
P (4, 1) and Q (0, –5) are points on the coordinate plane.
Determine the
a.(i) coordinates of M, the midpoint of P and Q.
(ii) gradient of the line drawn through P and Q.
(iii) gradient of the line drawn through M, perpendicular to PQ.[4]
Find k.[2]
▶️Answer/Explanation
Markscheme
a.(i) (2, – 2) parentheses not required. (A1)
(ii) gradient of PQ \( = \left( {\frac{{ – 5 – 1}}{{0 – 4}}} \right) = \frac{6}{4} = \frac{3}{2}(1.5)\) (M1)(A1)
(M1) for gradient formula with correct substitution
Award (A1) for \(y = \frac{3}{2}x – 5\) with no other working
(iii) gradient of perpendicular is \( – \frac{2}{3}\) (A1)(ft) (C4)[4 marks]
\(\left( {\frac{{k + 2}}{{0 – 2}}} \right) = – \frac{2}{3}\), \(k = – \frac{2}{3}\) or \(y = – \frac{2}{3}x + c\), \(c = – \frac{2}{3}\therefore k = – \frac{2}{3}\) (M1)(A1)(ft)
Allow (\(0, – \frac{2}{3}\))
(M1) is for equating gradients or substituting gradient into \(y = mx + c\) (C2)[2 marks]
Question
A store sells bread and milk. On Tuesday, 8 loaves of bread and 5 litres of milk were sold for $21.40. On Thursday, 6 loaves of bread and 9 litres of milk were sold for $23.40.
If \(b =\) the price of a loaf of bread and \(m =\) the price of one litre of milk, Tuesday’s sales can be written as \(8b + 5m = 21.40\).
a.Using simplest terms, write an equation in b and m for Thursday’s sales.[2]
b.Find b and m.[2]
c.Draw a sketch, in the space provided, to show how the prices can be found graphically.
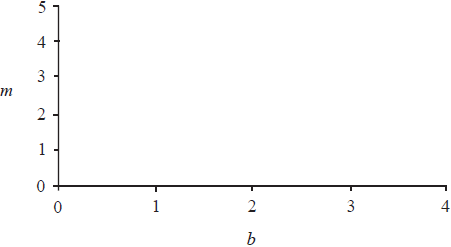 [2]
[2]
▶️Answer/Explanation
Markscheme
Thursday’s sales, \(6b + 9m = 23.40\) (A1)
\(2b + 3m = 7.80\) (A1) (C2)[2 marks]
\(m = 1.40\) (accept 1.4) (A1)(ft)
\(b = 1.80\) (accept 1.8) (A1)(ft)
Award (A1)(d) for a reasonable attempt to solve by hand and answer incorrect. (C2)[2 marks]
 (A1)(A1)(ft)
(A1)(A1)(ft)
(A1) each for two reasonable straight lines. The intersection point must be approximately correct to earn both marks, otherwise penalise at least one line.
Note: The follow through mark is for candidate’s line from (a). (C2)[2 marks]
