Question
Let \(f\) be a quadratic function. Part of the graph of \(f\) is shown below.
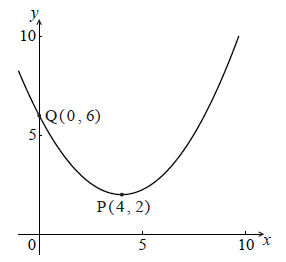
The vertex is at P(\(4\), \(2\)) and the y-intercept is at Q(\(0\), \(6\)) .
a.Write down the equation of the axis of symmetry.[1]
b.The function f can be written in the form \(f(x) = a{(x – h)^2} + k\) .
Write down the value of h and of k .[2]
c.The function f can be written in the form \(f(x) = a{(x – h)^2} + k\) .
Find a .[3]
▶️Answer/Explanation
Markscheme
a.\(x = 4\) (must be an equation) A1 N1
[1 mark]
\(h = 4\) , \(k = 2\) A1A1 N2
[2 marks]
attempt to substitute coordinates of any point on the graph into f (M1)
e.g. \(f(0) = 6\) , \(6 = a{(0 – 4)^2} + 2\) , \(f(4) = 2\)
correct equation (do not accept an equation that results from \(f(4) = 2\) ) (A1)
e.g. \(6 = a{( – 4)^2} + 2\) , \(6 = 16a + 2\)
\(a = \frac{4}{{16}}\left( { = \frac{1}{4}} \right)\) A1 N2
[3 marks]
Question
Let \(f(x) = \sin x + \frac{1}{2}{x^2} – 2x\) , for \(0 \le x \le \pi \) .
Let \(g\) be a quadratic function such that \(g(0) = 5\) . The line \(x = 2\) is the axis of symmetry of the graph of \(g\) .
The function \(g\) can be expressed in the form \(g(x) = a{(x – h)^2} + 3\) .
a.Find \(f'(x)\) .[3]
(ii) Find the value of \(a\) .[4]
d.Find the value of \(x\) for which the tangent to the graph of \(f\) is parallel to the tangent to the graph of \(g\) . [6]
▶️Answer/Explanation
Markscheme
a.\(f'(x) = \cos x + x – 2\) A1A1A1 N3
Note: Award A1 for each term.
[3 marks]
recognizing \(g(0) = 5\) gives the point (\(0\), \(5\)) (R1)
recognize symmetry (M1)
eg vertex, sketch
\(g(4) = 5\) A1 N3
[3 marks]
(i) \(h = 2\) A1 N1
(ii) substituting into \(g(x) = a{(x – 2)^2} + 3\) (not the vertex) (M1)
eg \(5 = a{(0 – 2)^2} + 3\) , \(5 = a{(4 – 2)^2} + 3\)
working towards solution (A1)
eg \(5 = 4a + 3\) , \(4a = 2\)
\(a = \frac{1}{2}\) A1 N2
[4 marks]
\(g(x) = \frac{1}{2}{(x – 2)^2} + 3 = \frac{1}{2}{x^2} – 2x + 5\)
correct derivative of \(g\) A1A1
eg \(2 \times \frac{1}{2}(x – 2)\) , \(x – 2\)
evidence of equating both derivatives (M1)
eg \(f’ = g’\)
correct equation (A1)
eg \(\cos x + x – 2 = x – 2\)
working towards a solution (A1)
eg \(\cos x = 0\) , combining like terms
\(x = \frac{\pi }{2}\) A1 N0
Note: Do not award final A1 if additional values are given.
[6 marks]
Question
Let \(f(x) = a{(x – h)^2} + k\). The vertex of the graph of \(f\) is at \((2, 3)\) and the graph passes through \((1, 7)\).
a.Write down the value of \(h\) and of \(k\). [2]
b.Find the value of \(a\).[3]
▶️Answer/Explanation
Markscheme
a.\(h = 2,{\text{ }}k = 3\) A1A1 N2
[2 marks]
attempt to substitute \((1,7)\) in any order into their \(f(x)\) (M1)
eg \(7 = a{(1 – 2)^2} + 3{\text{, }}7 = a{(1 – 3)^2} + 2{\text{, }}1 = a{(7 – 2)^2} + 3\)
correct equation (A1)
eg \(7 = a + 3\)
a = 4 A1 N2
[3 marks]
Question
The function f is given by
\(f(x)=\frac{2x+1}{x-3},x∈\mathbb{R}, x≠3\).
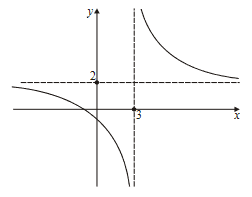
(a) (i) Show that y = 2 is an asymptote of the graph of y = f(x).
(ii) Find the vertical asymptote of the graph .
(iii) Write down the coordinates of the point P at which the asymptotes intersect.
(b) Find the points of intersection of the graph and the axes.
(c) Hence sketch the graph of y = f(x), showing the asymptotes by dotted lines.
▶️Answer/Explanation
Ans
(a) \(f(x)=\frac{2x+1}{x-2}=2+\frac{7}{x-3}\) or \(f(x)=\frac{2x+1}{x-3}=\frac{2+\frac{1}{x}}{1-\frac{3}{x}}\)
Therefore as |x|→∞ f(x) \(\Rightarrow \) y = 2 is an asymptote
OR \(\begin{matrix}
lim\\ x\rightarrow \infty\end{matrix} \frac{2x+1}{x-3}=2 \Rightarrow y = 2\) is an asymptote
(ii) Asymptote at x = 3
(iii) P(3,2)
(b) \(f(x)=0\Rightarrow x=-\frac{1}{2}(-\frac{1}{2},0)\) \(x=0 \Rightarrow f(x) = -\frac{1}{3}(0,-\frac{1}{3})\)
(c)