Question
Consider the function defined by f ( x ) = \(\frac{kx-5}{x-k}\), where x ∈ \(\mathbb{R}\) \ {k} and k2 ≠5 .
State the equation of the vertical asymptote on the graph of y = f ( x ) . [1]
State the equation of the horizontal asymptote on the graph of y = f ( x ) . [1]
Use an algebraic method to determine whether f is a self-inverse function. [4] Consider the case where k = 3 .
Sketch the graph of y = f ( x ) , stating clearly the equations of any asymptotes and the coordinates of any points of intersections with the coordinate axes. [3]
The region bounded by the x-axis, the curve y = f ( x ) , and the lines x = 5 and x = 7 is rotated through 2π about the x-axis. Find the volume of the solid generated, giving your answer in the form π ( a + b ln 2 ) , where a , b ∈ \(\mathbb{Z}\). [6]
▶️Answer/Explanation
Ans:
(a) x = k
(b) y = k
(c)
METHOD 1
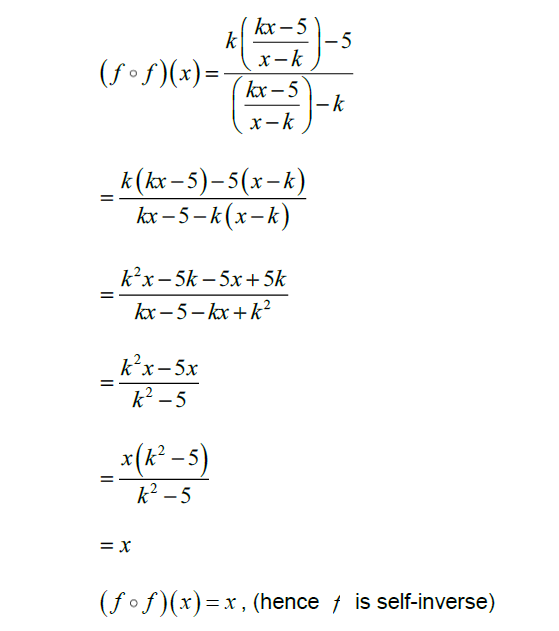
METHOD 2
(d)
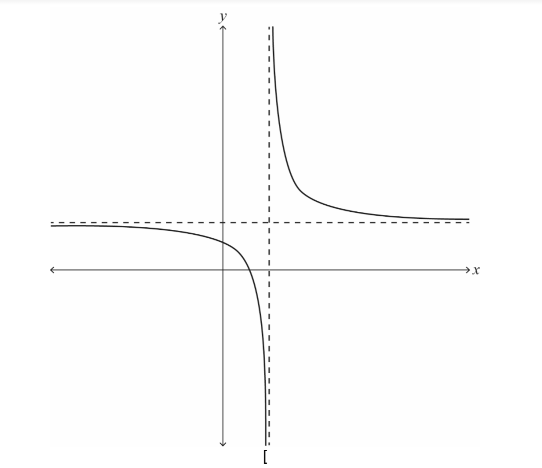
attempt to draw both branches of a rectangular hyperbola x=3 and y=3
(0,\(\frac{5}{3})and (\frac{5}{3}\),0)
(e)
METHOD 1
volume = \(\pi \int_{5}^{7}(\frac{3x-5}{x-3})^{2}\)dx
EITHER
attempt to express \(\frac{3x-5}{x-3} \)in the form \(p+ \frac{q}{x-3}\)
\(\frac{3x-5}{x-3}=3+\frac{4}{x-3}\)
OR attempt to expand
\((\frac{3x-5}{x-3})^{2}or (3x-5)^{2}\)and divide out
\((\frac{3x-5}{x-3})^{2} = 9+ \frac{24x-56}{(x-3)^{2}}\)
THEN
\((\frac{3x-5}{x-3})^{2}= 9+\frac{24}{x-3}+\frac{16}{(x-3)^{2}}\)
volume = \(\pi \int_{5}^{7}(9+\frac{24}{x-3}+\frac{16}{(x-3)^{2}})\)dx = \(\pi [9x+24ln(x-3)-\frac{16}{x-3}]^{7}_{5} =π [(63+ 24ln 4 − 4) − (45 + 24ln 2 −8)]=\pi (22+24ln2)\)
Question
The function f is defined by \(f(x) = \frac{{2x – 1}}{{x + 2}}\), with domain \(D = \{ x: – 1 \leqslant x \leqslant 8\} \).
a.Express \(f(x)\) in the form \(A + \frac{B}{{x + 2}}\), where \(A\) and \(B \in \mathbb{Z}\).[2]
(ii) Sketch the graph of \(y = f(x)\), showing the points of intersection with both axes.
(iii) On the same diagram, sketch the graph of \(y = f'(x)\).[8]
(ii) Find all solutions of the equation \(f(|x|) = – \frac{1}{4}\).[7]
▶️Answer/Explanation
Markscheme
by division or otherwise
\(f(x) = 2 – \frac{5}{{x + 2}}\) A1A1
[2 marks]
\(f'(x) = \frac{5}{{{{(x + 2)}^2}}}\) A1
> 0 as \({(x + 2)^2} > 0\) (on D) R1AG
Note: Do not penalise candidates who use the original form of the function to compute its derivative.
[2 marks]
\(S = \left[ { – 3,\frac{3}{2}} \right]\) A2
Note: Award A1A0 for the correct endpoints and an open interval.
[2 marks]
(i) EITHER
rearrange \(y = f(x)\) to make x the subject M1
obtain one-line equation, e.g. \(2x – 1 = xy + 2y\) A1
\(x = \frac{{2y + 1}}{{2 – y}}\) A1
OR
interchange x and y M1
obtain one-line equation, e.g. \(2y – 1 = xy + 2x\) A1
\(y = \frac{{2x + 1}}{{2 – x}}\) A1
THEN
\({f^{ – 1}}(x) = \frac{{2x + 1}}{{2 – x}}\) A1
Note: Accept \(\frac{5}{{2 – x}} – 2\)
(ii), (iii)
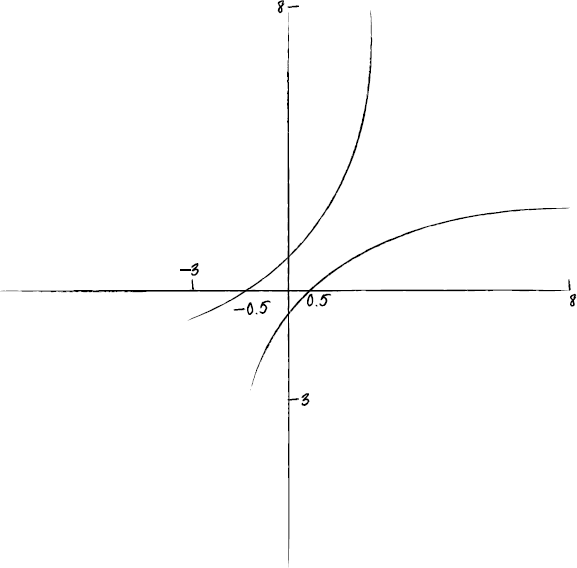A1A1A1A1
[8 marks]
Note: Award A1 for correct shape of \(y = f(x)\).
Award A1 for x intercept \(\frac{1}{2}\) seen. Award A1 for y intercept \( – \frac{1}{2}\) seen.
Award A1 for the graph of \(y = {f^{ – 1}}(x)\) being the reflection of \(y = f(x)\) in the line \(y = x\). Candidates are not required to indicate the full domain, but \(y = f(x)\) should not be shown approaching \(x = – 2\). Candidates, in answering (iii), can FT on their sketch in (ii).
(i)
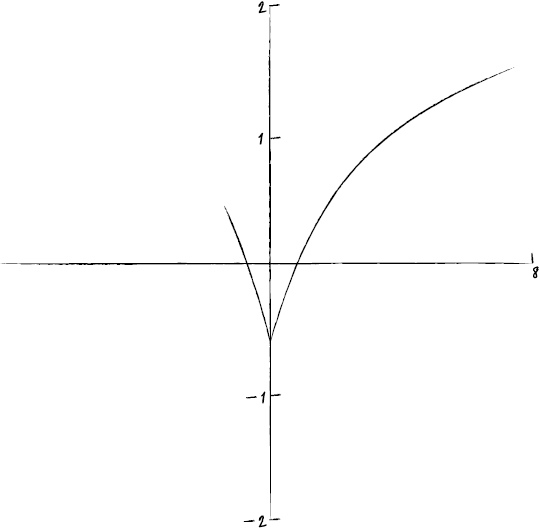A1A1A1
Note: A1 for correct sketch \(x > 0\), A1 for symmetry, A1 for correct domain (from –1 to +8).
Note: Candidates can FT on their sketch in (d)(ii).
(ii) attempt to solve \(f(x) = – \frac{1}{4}\) (M1)
obtain \(x = \frac{2}{9}\) A1
use of symmetry or valid algebraic approach (M1)
obtain \(x = – \frac{2}{9}\) A1
[7 marks]