Question:
The function f is defined by \(f(x)= \frac{4x+1}{x+4},\) where x ∈ R, x ≠ -4 .
(a) For the graph of f
(i) write down the equation of the vertical asymptote;
(ii) find the equation of the horizontal asymptote.
(b) (i) Find f -1(x).
(ii) Using an algebraic approach, show that the graph of f -1 is obtained by a reflection of the graph of f in the y-axis followed by a reflection in the x-axis.
The graphs of f and f -1 intersect at x = p and x = q, where p < q.
(c) (i) Find the value of p and the value of q.
(ii) Hence, find the area enclosed by the graph of f and the graph of f -1.
Answer/Explanation
Ans:
(a) (i) x =−4
(ii) attempt to substitute into \(\frac{a}{c}\) OR table with large values of x OR sketch of f showing asymptotic behaviour
y = 4
(b) (i) \(y=\frac{4x+1}{x+4},\)
attempt to interchange x and y (seen anywhere) 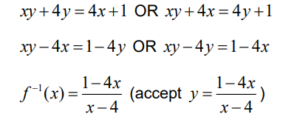
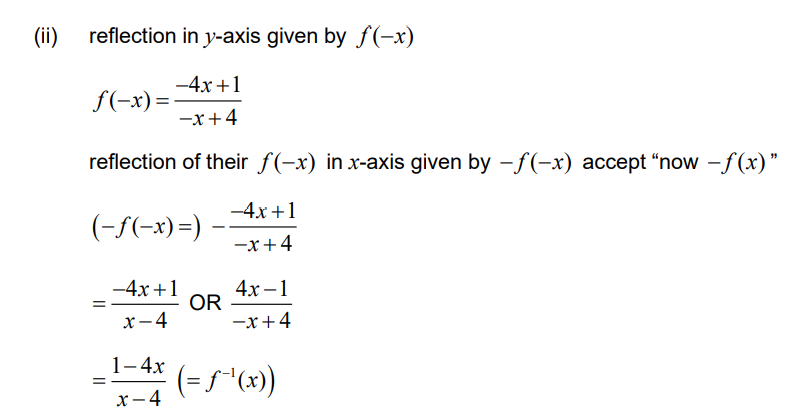
Note: If the candidate attempts to show the result using a particular coordinate on the graph of f rather than a general coordinate on the graph of f, where appropriate, award marks as follows:
M0A0 for eg (2,3) → (- 2,3)
M0A0 for ( -2,3) → ( -2, -3)
(c) (i) attempt to solve f(x) = f-1 (x) using graph or algebraically
p = −1 AND q =1
Note: Award (M1)A0 if only one correct value seen.
(ii) attempt to set up an integral to find area between f and f−1
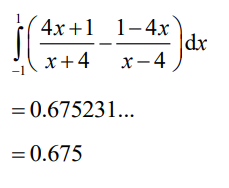
Question
Let \(f\left( x \right) = \frac{{8x – 5}}{{cx + 6}}\) for \(x \ne – \frac{6}{c},\,\,c \ne 0\).
The line x = 3 is a vertical asymptote to the graph of f. Find the value of c.
Write down the equation of the horizontal asymptote to the graph of f.
The line y = k, where \(k \in \mathbb{R}\) intersects the graph of \(\left| {f\left( x \right)} \right|\) at exactly one point. Find the possible values of k.
Answer/Explanation
Markscheme
valid approach (M1)
eg \(cx + 6 = 0,\,\, – \frac{6}{c} = 3\)
c = −2 A1 N2
[2 marks]
valid approach (M1)
eg \(\mathop {{\text{lim}}\,f}\limits_{x \to \infty } \left( x \right),\,\,y = \frac{8}{c}\)
y = −4 (must be an equation) A1 N2
[2 marks]
valid approach to analyze modulus function (M1)
eg sketch, horizontal asymptote at y = 4, y = 0
k = 4, k = 0 A2 N3
[3 marks]
Question
Let \(f(x) = \frac{{3x}}{{x – q}}\), where \(x \ne q\).
Write down the equations of the vertical and horizontal asymptotes of the graph of \(f\).
The vertical and horizontal asymptotes to the graph of \(f\) intersect at the point \({\text{Q}}(1,3)\).
Find the value of \(q\).
The vertical and horizontal asymptotes to the graph of \(f\) intersect at the point \({\text{Q}}(1,3)\).
The point \({\text{P}}(x,{\text{ }}y)\) lies on the graph of \(f\). Show that \({\text{PQ}} = \sqrt {{{(x – 1)}^2} + {{\left( {\frac{3}{{x – 1}}} \right)}^2}} \).
The vertical and horizontal asymptotes to the graph of \(f\) intersect at the point \({\text{Q}}(1,3)\).
Hence find the coordinates of the points on the graph of \(f\) that are closest to \((1,3)\).
Answer/Explanation
Markscheme
\(x = q,{\text{ }}y = 3\) (must be equations) A1A1 N2
[2 marks]
recognizing connection between point of intersection and asymptote (R1)
eg \(x = 1\)
\(q = 1\) A1 N2
[2 marks]
correct substitution into distance formula A1
eg \(\sqrt {{{(x – 1)}^2} + {{(y – 3)}^2}} \)
attempt to substitute \(y = \frac{{3x}}{{x – 1}}\) (M1)
eg \(\sqrt {{{(x – 1)}^2} + {{\left( {\frac{{3x}}{{x – 1}} – 3} \right)}^2}} \)
correct simplification of \(\left( {\frac{{3x}}{{x – 1}} – 3} \right)\) (A1)
eg \(\frac{{3x – 3x(x – 1)}}{{x – 1}}\)
correct expression clearly leading to the required answer A1
eg \(\frac{{3x – 3x + 3}}{{x – 1}},{\text{ }}\sqrt {{{(x – 1)}^2} + {{\left( {\frac{{3x – 3x + 3}}{{x – 1}}} \right)}^2}} \)
\({\text{PQ}} = \sqrt {{{(x – 1)}^2} + {{\left( {\frac{3}{{x – 1}}} \right)}^2}} \) AG N0
[4 marks]
recognizing that closest is when \({\text{PQ}}\) is a minimum (R1)
eg sketch of \({\text{PQ}}\), \(({\text{PQ}})'(x) = 0\)
\(x = – 0.73205{\text{ }}x = 2.73205\) (seen anywhere) A1A1
attempt to find y-coordinates (M1)
eg \(f( – 0.73205)\)
\((-0.73205, 1.267949) , (2.73205, 4.73205)\)
\((-0.732, 1.27) , (2.73, 4.73) \) A1A1 N4
[6 marks]
