Question
Consider the three planes
∏1 : 2x – y + z = 4
∏2 : x – 2y + 3z = 5
∏3 : -9x + 3y – 2z = 32
(a) Show that the three planes do not intersect.
(b) (i) Verify that the point P(1 , -2 , 0) lies on both ∏1 and ∏2 .
(ii) Find a vector equation of L, the line of intersection of ∏1 and ∏2 .
(c) Find the distance between L and ∏3 .
▶️Answer/Explanation
Ans:
(a) METHOD 1
attempt to eliminate a variable
obtain a pair of equations in two variables
EITHER
-3x + z = -3 and
-3x + z = 44
OR
-5x + y = -7 and
-5x + y = 40
OR
3x – z = 3 and
3x – z = \(\frac{79}{5}\)
THEN
the two lines are parallel ( – 3 ≠ 44 or – 7 ≠ 40 or 3 ≠ -\(\frac{79}{5}\)
Note: There are other possible pairs of equations in two variables.
To obtain the final R1, at least the initial M1 must have been awarded.
hence the three planes do not intersect
METHOD 2
vector product of the two normals = \(\begin{pmatrix}-1\\-5\\-3\end{pmatrix}\) (or equivalent)
\(r = \begin{pmatrix}1\\-2 \\0 \end{pmatrix} + \lambda \begin{pmatrix}1\\5 \\3 \end{pmatrix}\) (or equivalent)
Note: Award A0 if “r =” is missing. Subsequent marks may still be awarded.
Attempt to substitute (1 + λ, -2 + 5λ, 3λ) in ∏3
-9(1 + λ) + 3(-2+5λ) – 2(3λ) = 32
− 15 = 32, a contradiction
hence the three planes do not intersect
(b) (i) ∏1 : 2 + 2 + 0 = 4 and ∏2 : 1 + 4 + 0 = 5
(ii) METHOD 1
attempt to find the vector product of the two normals
\(\begin{pmatrix}2\\-1 \\1 \end{pmatrix} \times \begin{pmatrix}1\\-2 \\3 \end{pmatrix}\)
\(=\begin{pmatrix}-1\\-5 \\-3 \end{pmatrix}\)
\(r = \begin{pmatrix}1\\-2 \\0 \end{pmatrix} + \lambda \begin{pmatrix}1\\5 \\3 \end{pmatrix}\)
Note: Award A1A0 if “r =” is missing.
Accept any multiple of the direction vector.
Working for (b)(ii) may be seen in part (a) Method 2. In this case penalize
lack of “r =” only once.
METHOD 2
attempt to eliminate a variable from ∏1 and ∏2
3x – z = 3 OR 3y – 5z = -6 OR 5x – y = 7
Let x = t
substituting x = t in 3x – z = 3 to obtain
z = -3 + 3t and y = 5t – 7 (for all three variables in parametric form)
\(r = \begin{pmatrix}1\\-2 \\0 \end{pmatrix} + \lambda \begin{pmatrix}1\\5 \\3 \end{pmatrix}\)
Note: Award A1A0 if “r =” is missing.
Accept any multiple of the direction vector. Accept other position vectors
which satisfy both the planes ∏1 and ∏2 .
(c) METHOD 1
the line connecting L and ∏3 is given by L1
attempt to substitute position and direction vector to form L1
\(s = \begin{pmatrix}1\\-2 \\0 \end{pmatrix} + t \begin{pmatrix}-9\\3 \\-2 \end{pmatrix}\)
substitute (1 – 9t, – 2 + 3t, – 2t) in ∏3
-9(1-9t) + 3(-2+3t) – 2(-2t) = 32
\(94t = 47\Rightarrow t=\frac{1}{2}\)
attempt to find distance between (1, -2,0) and their point \(\begin{pmatrix}-\frac{7}{2}, & -\frac{1}{2}, & -1 \end{pmatrix}\)
\(=\left | \begin{pmatrix}1\\-2 \\0 \end{pmatrix} +\frac{1}{2}\begin{pmatrix}-9\\3 \\-2 \end{pmatrix}-\begin{pmatrix}1\\-2 \\0 \end{pmatrix}\right | = \frac{1}{2}\sqrt{(-9)^{2}+3^{2}+(-2)^{2}}\)
\(=\frac{\sqrt{94}}{2}\)
METHOD 2
unit normal vector equation of ∏3 is given by 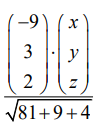
\(=\frac{32}{\sqrt{94}}\)

Question
A company is designing a new logo. The logo is created by removing two equal segments from a rectangle, as shown in the following diagram.
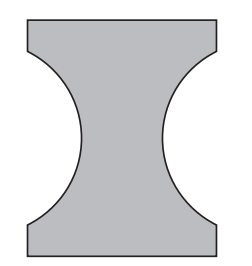
The rectangle measures 5cm by 4cm. The points A and B lie on a circle, with centre O and radius 2cm, such that AÔB = θ, where 0 < θ < π. This information is shown in the following diagram.
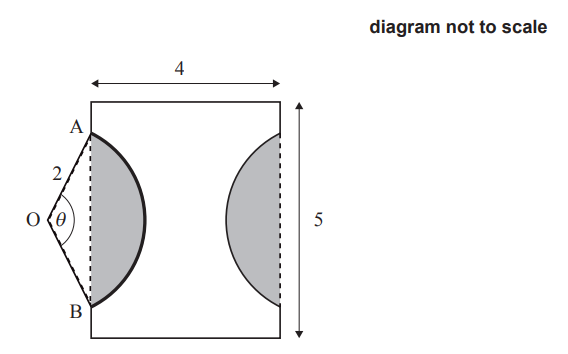
(a) Find the area of one of the shaded segments in terms of θ.
(b) Given that the area of the logo is 13.4cm2, find the value of θ.
▶️Answer/Explanation
Ans:
(a) valid approach to find area of segment by finding area of sector – area of triangle
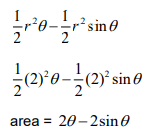
(b) EITHER
area of logo = area of rectangle – area of segments
5 × 4 – 2 × (2θ – 2sin θ) = 13.4
OR
area of one segment = \(\frac{20-13.4}{2}(=3.3)\)
2θ – 2sinθ = 3.3
THEN
θ = 2.35672….
θ = 2.36 (do not accept an answer in degrees)
Note: Award (M1)(A1)A0 if there is more than one solution.
Award (M1)(A1FT)A0 if the candidate works in degrees and obtains a final answer of 135.030…
Question
For a right pyramid of square base of slide 8 and vertical height 3 find
(a) the volume
(b) the surface are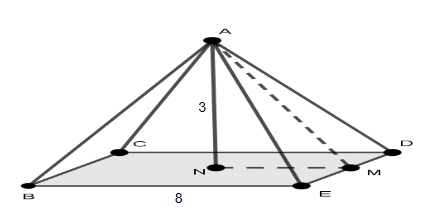
▶️Answer/Explanation
Ans
(a) \(V=\frac{1}{3}8^23=64\)
(b) \(AM^2=4^2+3^2 \Rightarrow AM =5\)
\(S=8^2+4 \times (\frac{1}{2} \times 8 \times 5)=64+80=144\)
Question
Two boats A and B start moving from the same point P. Boat A moves in a straight line at 20 km h-1 and boat B moves in a straight line at 32 km h-1. The angle between their paths is 70o. Find the distance between the boats after 2.5 hours.
▶️Answer/Explanation
Ans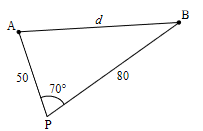
\((2.5 \times 20 = 50)\) \((2.5 \times 32=80)\)
\(d^2=50^2 + 80^2 – 2 \times 50 \times 80 \times cos 70^o\)
d = 78.5 km
Question
There is a vertical tower TA of height 36m at the base A of a hill. A straight path goes up the hill from A to a point U. This information is represented by the following diagram.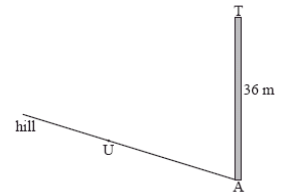
The path makes a 4o angle with the horizontal.
The point U on the path is 25 m away from the base of the tower.
The top of the tower is fixed to U by a wire of length x m.
(a) Complete the diagram, showing clearly all the information above.
(b) Find x.
▶️Answer/Explanation
Ans
(a)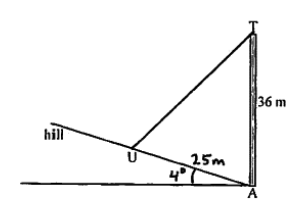
(b) \(TAU = 86^o\)
\(x^2=25^2+36^2 – 2(25)(36) cos 86^0\)
\(x=42.4\)
Question
The diagram shows a vertical pole PQ, which is supported by two wires fixed to the horizontal ground at A and B.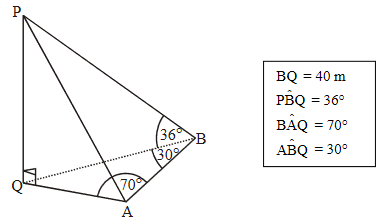
Find
(a) the height of the pole, PQ;
(b) the distance between A and B.
▶️Answer/Explanation
Ans
(a) \(\frac{PQ}{40}=tan 36^o \Rightarrow PQ≈29.1 m (3sf)\)
(b)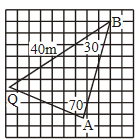
\(AQB = 80^o\)
\(\frac{AB}{sin80^o}=\frac{40}{sin70^o} \Rightarrow AB = 41.9m (3sf)\)
Question
A ship leaves port A on a bearing of 030o.It sails a distance of 25 km to point B. At B, the ship changes direction to a bearing of 100°. It sails a distance of 40 km to reach point C. This information is shown in the diagram below.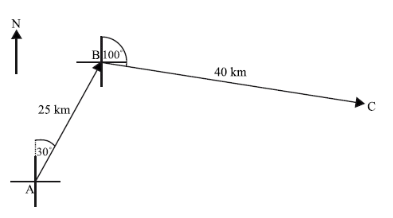
A second ship leaves port A and sails directly to C.
(a) Find the distance the second ship will travel
(b) Find the bearing of the course taken by the second ship.
▶️Answer/Explanation
Ans
(a) \(ABC=110^o\)
\(AC^2=25^2+40^2-2(25)(40)cos110^o \Rightarrow AC=53.9 (km)\)
(b) By using either sine rule or cosine rule: \(BAC=44.2^o \Rightarrow bearing = 074^o\)
Question
The following diagram shows a pentagon ABCDE, with AB = 9.2 cm, BC = 3.2 cm, BD = 7.1 cm, AED = 110o, ADE = 52o and ABD = 60o.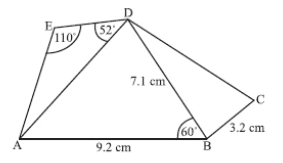
(a) Find AD
(b) Find DE
(c) The area of triangle BCD is 5.68 cm2. Find DBC.
(d) Find AC.
(e) Find the area of quadrilateral ABCD.
▶️Answer/Explanation
Ans
(a) \((AD)^2=7.1^2+9.2^2-2(7.1)(9.2) cos 60^o \Rightarrow AD=8.35 (cm)\)
(b) \(180^o – 162^o=18^o\)
\(\frac{DE}{sin18^o}=\frac{8.35}{sin 110^o} \Rightarrow DE = 2.75 (cm)\)
(c) \(5.68=\frac{1}{2}(3.2)(7.1)sin DBC \Rightarrow sin DBC = 0.5 \Rightarrow DBC 30^o and/or 150^o\)
(d) Finding \(ABC (60^o+DBC)\)
\((AC)^2=(AB)^2+(BC)^2 \Rightarrow (AC)^2 = 9.2^2 + 3.2^2 \Rightarrow AC = 9.74 (cm)\)
(e) Area \(=\frac{1}{2} \times 9.2 \times 7.1 sin 60^o = 28.28…\)
Area of ABCD \(=28.28… + 5.68 = 34.0(cm^2)\)
Question
In the diagram below, the points O(0,0) and A(8,6) are fixed. The angle OPA varies as the point P(x,10) moves along the horizontal line y = 10.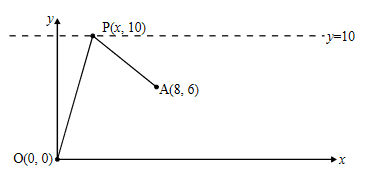
(a) (i) Show that \(AP=\sqrt{x^2-16x+80}\).
(ii) Write down a similar expression for OP in terms of x.
(b) Hence, show that cos OPA=\(\frac{x^2-8x+40}{\sqrt{{(x^2-16x+80)(x^2+100)}}}\)
(c) Find, in degrees, the angle OPA when x = 8.
(d) Find the positive value of x such that OPA = 60o.
Let the function f be defined by
\(f(x)=cos OPA=\frac{x^2-8x+40}{\sqrt{{(x^2-16x+80)(x^2+100)}}}\), 0≤x≤15\).
(e) Consider the equation f(x)=1
(i) Explain, in terms of the position of the points O, A and P, why this equation has a solution.
(ii) Find the exact solution to the equation.
▶️Answer/Explanation
Ans
(a) (i) \(AP=\sqrt{(x-8)^2+(10-6)^2}=\sqrt{x^2-16x+80}\)
(ii) \(OP=\sqrt{(x-0)^2+(10-0)^2}=\sqrt{x^2+100}\)
(b) \(cos OPA=\frac{AP^2+OP^2-OA^2}{2AP \times OP}=\frac{(x^2-16x+80)+(x^2+100)-(8^2+6^2)}{2\sqrt{x^2-16x+80}\sqrt{x^2+100}}\)
\(=\frac{2x^2-16x+80}{2\sqrt{x^2-16x+80}\sqrt{x^2+100}}=\frac{x^2-8x+40}{\sqrt{{(x^2-16x+80)(x^2+100)}}}\)
(c) For \(x = 8, cos OPA=0.780869 \Rightarrow OPA = 38.7^o (3sf)\)
OR \(tanOPA=\frac{8}{10} \Rightarrow OPA=38.7^o (3sf)\)
(d) \(OPA=60^o \Rightarrow cos OPA = 0.5\)
\(0.5=\frac{x^2-8x+40}{\sqrt{{(x^2-16x+80)(x^2+100)}}} \Rightarrow x = 5.63\)
(e) (i) f(x) = 1 when cosOPA = 1, hence, when OPA = 0.
This occurs when the points O, A, P are collinear.
(ii) The line (OA) has equation \(y=\frac{3x}{4}\) When y = 10, \(x=\frac{40}{3}(=13\frac{1}{3})\)
OR directly \(x=\frac{40}{3}(=13\frac{1}{3})\)
Question
An office tower is in the shape of a cuboid with a square base. The roof of the tower is in the shape of a square based right pyramid.
The diagram shows the tower and its roof with dimensions indicated. The diagram is not drawn to scale.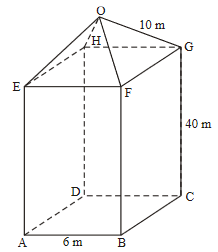
(a) Calculate, correct to three significant figures,
(i) the size of the angle between OF and FG;
(ii) the shortest distance from O to FG;
(iii) the total surface area of the four triangular sections of the roof;
(iv) the size of the angle between the slant height of the roof and the plane EFGH;
(v) the height of the tower from the base to O.
A parrot’s nest is perched at a point, P, on the edge, BF, of the tower. A person at the point A, outside the building, measures the angle of elevation to point P to be 79°.
(b) Find, correct to three significant figures, the height of the nest from the base of the tower.
▶️Answer/Explanation
Ans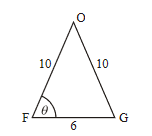
(a) (i) \(cos\theta=(\frac{10^2+6^2-10^2}{(2)(10)(6)} \Rightarrow \theta = 72.5^o (3sf)\)
(ii) h = shortest distance from O to FG \(= 3 tan \theta = 9.53939…=9.54m(3sf)\)
(iii) Area of ΔOFG \(=\frac{1}{2} (10)(6)(sin \theta)\)
toatal surface area of roof \(=4 \times \frac{1}{2}(10)(6)(sin \theta)=114.4727…=114m^2(3s.f.)\)
(iv) Let Φ = angle between slant height (line) and plane EFGH
\(cos \phi =(\frac{3}{h}) \Rightarrow \phi = 71.7^o (3 s.f)\)
(v) H = Height of tower from base to \(O =40+ \sqrt{h^2-3^2}=49.1m(3s.f)\)
(b) Height (BP) \(=\frac{6sin79^o}{sin(90^o-79^o)}=30.9 m(3 s.f.)\)
Question
Consider the following diagram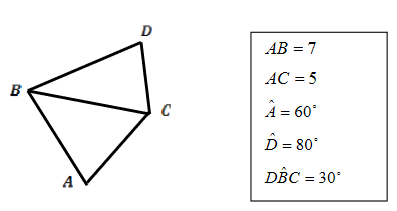
Find
(a) the length of the side BD.
(b )the area of the quadrilateral ABDC.
(c) the perimeter of the quadrilateral ABCD.
It is given that the bearing from B to D is 70o. Find
(d) the bearing from B to A.
(e) the bearing from A to B.
▶️Answer/Explanation
Ans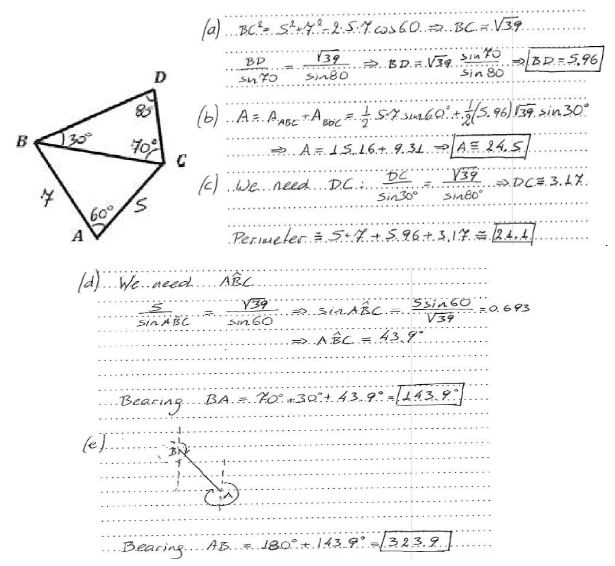
Question
The following three dimensional diagram shows the four points A,B,C and D. A,B,C are in the same horizontal plane and AD is vertical. The ABC is 45o , and BC = 50m. The angle of elevation from point B to point D is 30o, while the angle of elevation from point C to point D is 20o.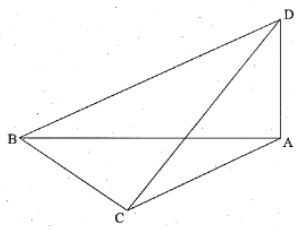
Using the cosine rule in the triangle ABC, or otherwise, find AD.
▶️Answer/Explanation
Ans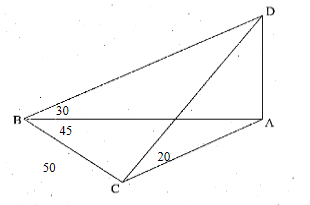
Let h = AD. \(Ab = \frac{h}{tan30}, AC=\frac{h}{tan20}\)
\((\frac{h}{tan20})^2=(\frac{h}{tan30})^2+50^2-100(\frac{h}{tan30})\frac{\sqrt{2}}{2}\Rightarrow h = 13.6\)
Question
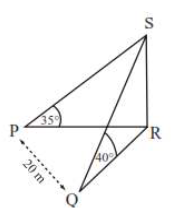
The above three dimensional diagram shows the points P and Q which are respectively west and south-west of the base R of a vertical flagpole RS on horizontal ground. The angles of elevation of the top S of the flagpole from P and Q are respectively 35o and 40o, and PQ = 20 m.
Determine the height of the flagpole.
▶️Answer/Explanation
Ans
PR = htan 55o, QR = htan50o where RS = h
Use the cosine rule in triangle PQR.
\(20^2=h^2tan^255^o+h^2tan^250^o-2htan55^ocos45^o\)
\(h^2=\frac{400}{tan^255^o+tan^250^o-2tan55^ocos45^o}\)
=379.9…..
h = 19.5 (m)
