IBDP Maths SL 3.1 The distance between two points AA HL Paper 2- Exam Style Questions- New Syllabus
Question
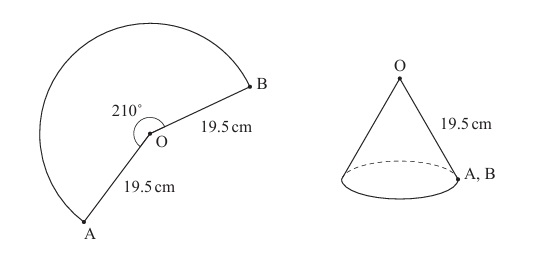
(b) Determine the radius of the base of the cone formed from the sector.
Most-appropriate topic codes (IB Mathematics: Analysis and Approaches HL 2025):
• SL 3.1: Geometry of 3D shapes: Cones — part (b)
▶️ Answer/Explanation
(a)
To find the area of the sector, the angle must be in radians or the degree formula can be used.
Method 1 (Radians):
Convert \( 210^\circ \) to radians: \( 210^\circ = \frac{210\pi}{180} = \frac{7\pi}{6} \) radians.
Area of sector formula: \( A = \frac{1}{2} r^2 \theta \).
\( A = \frac{1}{2} (19.5)^2 \left( \frac{7\pi}{6} \right) \)
Method 2 (Degrees):
Area of sector formula: \( A = \frac{\theta}{360} \pi r^2 \).
\( A = \frac{210}{360} \pi (19.5)^2 \)
Both methods yield the same calculation: \( A = \frac{3549\pi}{16} \approx 696.844\dots \)
Rounded to three significant figures: \( \boxed{697 \, \text{cm}^2} \)
(b)
The arc length \( AB \) of the sector becomes the circumference of the base of the cone.
Step 1: Find the arc length.
Arc length \( s = r \theta \) (with \( \theta \) in radians).
\( s = 19.5 \times \frac{7\pi}{6} = \frac{91\pi}{4} \approx 71.4712 \, \text{cm} \)
Step 2: Relate arc length to cone base circumference.
Let \( r_c \) be the radius of the cone’s base. Then: \( 2\pi r_c = s \)
\( 2\pi r_c = 71.4712\dots \)
\( r_c = \frac{71.4712\dots}{2\pi} \approx 11.375 \)
Rounded to three significant figures: \( \boxed{11.4 \, \text{cm}} \)