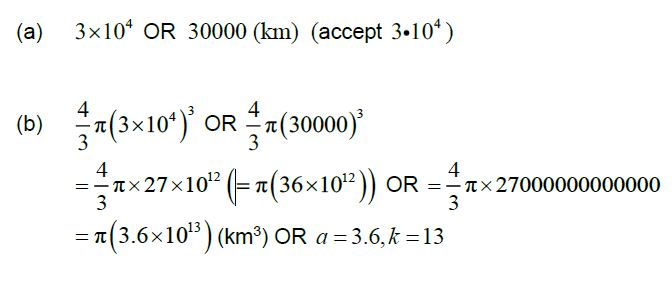Question: [Maximum mark: 6]
A company is designing a new logo. The logo is created by removing two equal segments from a rectangle, as shown in the following diagram.
The rectangle measures 5cm by 4cm. The points A and B lie on a circle, with centre O and radius 2cm, such that AÔB = θ, where 0 < θ < π. This information is shown in the following diagram.
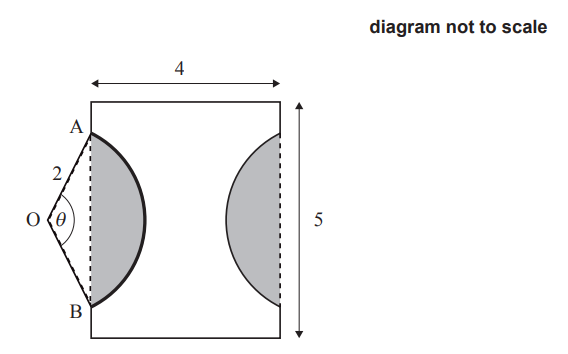
(a) Find the area of one of the shaded segments in terms of θ.
(b) Given that the area of the logo is 13.4cm2, find the value of θ.
▶️Answer/Explanation
Ans:
(a) valid approach to find area of segment by finding area of sector – area of triangle
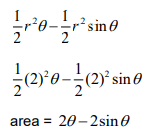
(b) EITHER
area of logo = area of rectangle – area of segments
5 × 4 – 2 × (2θ – 2sin θ) = 13.4
OR
area of one segment = \(\frac{20-13.4}{2}(=3.3)\)
2θ – 2sinθ = 3.3
THEN
θ = 2.35672….
θ = 2.36 (do not accept an answer in degrees)
Note: Award (M1)(A1)A0 if there is more than one solution.
Award (M1)(A1FT)A0 if the candidate works in degrees and obtains a final answer of 135.030…
Question
The diameter of a spherical planet is 6 x 104 km .
(a) Write down the radius of the planet.[1]
The volume of the planet can be expressed in the form π(a × 10k) km3 where 1 ≤ a <10 and k ∈ \(\mathbb{Z}\)
(b) Find the value of a and the value of k . [3]
▶️Answer/Explanation
Ans