IBDP Maths SL 3.3 Applications of trigonometry AA HL Paper 1- Exam Style Questions- New Syllabus
The following diagram shows a circle with centre \( O \) and radius \( 4 \, \text{cm} \).
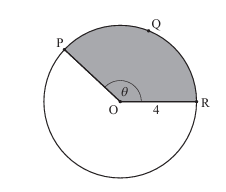
The points \( P \), \( Q \), and \( R \) lie on the circumference of the circle, and \( \angle POR = \theta \), where \( \theta \) is measured in radians. The length of arc \( PQR \) is \( 10 \, \text{cm} \).
Part (a):
Find the perimeter of the shaded sector. [2]
Part (b):
Find \( \theta \). [2]
Part (c):
Find the area of the shaded sector. [2]
▶️ Answer/Explanation
Part (a)
Find the perimeter of the shaded sector \( POR \).
The perimeter of the sector includes the arc \( PQR \) and the radii \( OP \) and \( OR \).
Given: Arc length \( PQR = 10 \, \text{cm} \), radius \( OP = OR = 4 \, \text{cm} \).
Perimeter = Arc \( PQR + OP + OR \):
\[ 10 + 4 + 4 = 18 \, \text{cm} \]
Answer: The perimeter of the shaded sector is \( 18 \, \text{cm} \).
Part (b)
Find \( \theta \).
Use the arc length formula: \( \text{Arc length} = r \theta \).
Given: Arc \( PQR = 10 \, \text{cm} \), radius \( r = 4 \, \text{cm} \).
\[ 10 = 4 \theta \]
\[ \theta = \frac{10}{4} = 2.5 \, \text{radians} \]
Answer: \( \theta = 2.5 \, \text{radians} \)
Part (c)
Find the area of the shaded sector \( POR \).
Use the sector area formula: \( \text{Area} = \frac{1}{2} r^2 \theta \).
Given: \( r = 4 \, \text{cm} \), \( \theta = 2.5 \, \text{radians} \) (from part b).
\[ \text{Area} = \frac{1}{2} \cdot 4^2 \cdot 2.5 = \frac{1}{2} \cdot 16 \cdot 2.5 = 8 \cdot 2.5 = 20 \, \text{cm}^2 \]
Answer: The area of the shaded sector is \( 20 \, \text{cm}^2 \).
ABCD is a quadrilateral where AB = 6.5, BC = 9.1, CD = 10.4, DA = 7.8 and ∠CDA = 90°.
Find ∠ABC to the nearest degree.
▶️ Answer/Explanation
Explanation:
Step 1: Find diagonal AC
Using Pythagoras’ theorem in right-angled ΔCDA:
\[ AC = \sqrt{DA^2 + CD^2} = \sqrt{7.8^2 + 10.4^2} = 13 \]
Step 2: Apply cosine rule
In ΔABC, using the cosine rule for ∠ABC:
\[ \cos B = \frac{AB^2 + BC^2 – AC^2}{2 \times AB \times BC} = \frac{6.5^2 + 9.1^2 – 13^2}{2 \times 6.5 \times 9.1} \] \[ \cos B = \frac{-43.94}{118.3} ≈ -0.3714 \]
Step 3: Calculate angle
\[ ∠ABC = \cos^{-1}(-0.3714) ≈ 111.8° \] Rounded to nearest degree: \[ \boxed{112°} \]
Markscheme:
• Correct use of Pythagoras (M1)
• AC = 13 (A1)
• Correct cosine rule setup (M1)
• ∠ABC = 111.8° (A1)
• 112° A1
[5 marks]
