Question
Use mathematical induction to prove that \(\frac{d^n}{dx^n}\) ( xepx) = pn-1 ( px+n) epx
for n for n ∈ \(\mathbb{Z^+}\) , p ∈ \(\mathbb{Q}\).
▶️Answer/Explanation
Ans
\(n=1:LHS=\) 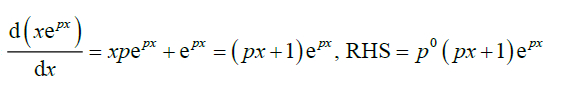
LHS = RHS = so true for \(n =1 ;\)
assume proposition true for \(n=k,i.e.\) 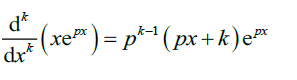
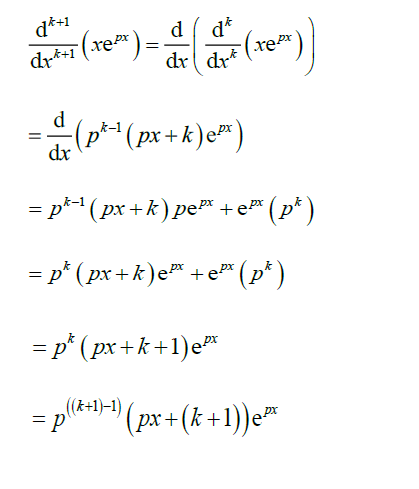
hence true for \(n =1\) and \(n = k\) true
⇒\(n = k +1\) true
therefore true for all n ∈ \(\mathbb{Z^+}\)
Question
Prove by mathematical induction that, for \(n \in {\mathbb{Z}^ + }\),
\[1 + 2\left( {\frac{1}{2}} \right) + 3{\left( {\frac{1}{2}} \right)^2} + 4{\left( {\frac{1}{2}} \right)^3} + … + n{\left( {\frac{1}{2}} \right)^{n – 1}} = 4 – \frac{{n + 2}}{{{2^{n – 1}}}}.\][8]
(a) Using integration by parts, show that \(\int {{{\text{e}}^{2x}}\sin x{\text{d}}x = \frac{1}{5}{{\text{e}}^{2x}}} (2\sin x – \cos x) + C\) .
(b) Solve the differential equation \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \sqrt {1 – {y^2}} {{\text{e}}^{2x}}\sin x\), given that y = 0 when x = 0,
writing your answer in the form \(y = f(x)\) .
(c) (i) Sketch the graph of \(y = f(x)\) , found in part (b), for \(0 \leqslant x \leqslant 1.5\) .
Determine the coordinates of the point P, the first positive intercept on the x-axis, and mark it on your sketch.
(ii) The region bounded by the graph of \(y = f(x)\) and the x-axis, between the origin and P, is rotated 360° about the x-axis to form a solid of revolution.
Calculate the volume of this solid.[17]
▶️Answer/Explanation
Markscheme
prove that \(1 + 2\left( {\frac{1}{2}} \right) + 3{\left( {\frac{1}{2}} \right)^2} + 4{\left( {\frac{1}{2}} \right)^3} + … + n{\left( {\frac{1}{2}} \right)^{n – 1}} = 4 – \frac{{n + 2}}{{{2^{n – 1}}}}\)
for n = 1
\({\text{LHS}} = 1,{\text{ RHS}} = 4 – \frac{{1 + 2}}{{{2^0}}} = 4 – 3 = 1\)
so true for n = 1 R1
assume true for n = k M1
so \(1 + 2\left( {\frac{1}{2}} \right) + 3{\left( {\frac{1}{2}} \right)^2} + 4{\left( {\frac{1}{2}} \right)^3} + … + k{\left( {\frac{1}{2}} \right)^{k – 1}} = 4 – \frac{{k + 2}}{{{2^{k – 1}}}}\)
now for n = k +1
LHS: \(1 + 2\left( {\frac{1}{2}} \right) + 3{\left( {\frac{1}{2}} \right)^2} + 4{\left( {\frac{1}{2}} \right)^3} + … + k{\left( {\frac{1}{2}} \right)^{k – 1}} + (k + 1){\left( {\frac{1}{2}} \right)^k}\) A1
\( = 4 – \frac{{k + 2}}{{{2^{k – 1}}}} + (k + 1){\left( {\frac{1}{2}} \right)^k}\) M1A1
\( = 4 – \frac{{2(k + 2)}}{{{2^k}}} + \frac{{k + 1}}{{{2^k}}}\,\,\,\,\,\)(or equivalent) A1
\( = 4 – \frac{{(k + 1) + 2}}{{{2^{(k + 1) – 1}}}}\,\,\,\,\,\)(accept \(4 – \frac{{k + 3}}{{{2^k}}}\)) A1
Therefore if it is true for n = k it is true for n = k + 1. It has been shown to be true for n = 1 so it is true for all \(n{\text{ }}( \in {\mathbb{Z}^ + })\). R1
Note: To obtain the final R mark, a reasonable attempt at induction must have been made.
[8 marks]
(a)
METHOD 1
\(\int {{{\text{e}}^{2x}}\sin x{\text{d}}x = – \cos x{{\text{e}}^{2x}} + \int {2{{\text{e}}^{2x}}\cos x{\text{d}}x} } \) M1A1A1
\( = – \cos x{{\text{e}}^{2x}} + 2{{\text{e}}^{2x}}\sin x – \int {4{{\text{e}}^{2x}}\sin x{\text{d}}x} \) A1A1
\(5\int {{{\text{e}}^{2x}}\sin x{\text{d}}x = – \cos x{{\text{e}}^{2x}} + 2{{\text{e}}^{2x}}\sin x} \) M1
\(\int {{{\text{e}}^{2x}}\sin x{\text{d}}x = \frac{1}{5}{{\text{e}}^{2x}}(2\sin x – \cos x) + C} \) AG
METHOD 2
\(\int {\sin x{{\text{e}}^{2x}}{\text{d}}x = \frac{{\sin x{{\text{e}}^{2x}}}}{2} – \int {\cos x\frac{{{{\text{e}}^{2x}}}}{2}{\text{d}}x} } \) M1A1A1
\( = \frac{{\sin x{{\text{e}}^{2x}}}}{2} – \cos x\frac{{{{\text{e}}^{2x}}}}{4} – \int {\sin x\frac{{{{\text{e}}^{2x}}}}{4}{\text{d}}x} \) A1A1
\(\frac{5}{4}\int {{{\text{e}}^{2x}}\sin x{\text{d}}x = \frac{{{{\text{e}}^{2x}}\sin x}}{2} – \frac{{\cos x{{\text{e}}^{2x}}}}{4}} \) M1
\(\int {{{\text{e}}^{2x}}\sin x{\text{d}}x = \frac{1}{5}{{\text{e}}^{2x}}(2\sin x – \cos x) + C} \) AG
[6 marks]
(b)
\(\int {\frac{{{\text{d}}y}}{{\sqrt {1 – {y^2}} }} = \int {{{\text{e}}^{2x}}\sin x{\text{d}}x} } \) M1A1
\(\arcsin y = \frac{1}{5}{{\text{e}}^{2x}}(2\sin x – \cos x)( + C)\) A1
when \(x = 0,{\text{ }}y = 0 \Rightarrow C = \frac{1}{5}\) M1
\(y = \sin \left( {\frac{1}{5}{{\text{e}}^{2x}}(2\sin x – \cos x) + \frac{1}{5}} \right)\) A1
[5 marks]
(c)
(i) 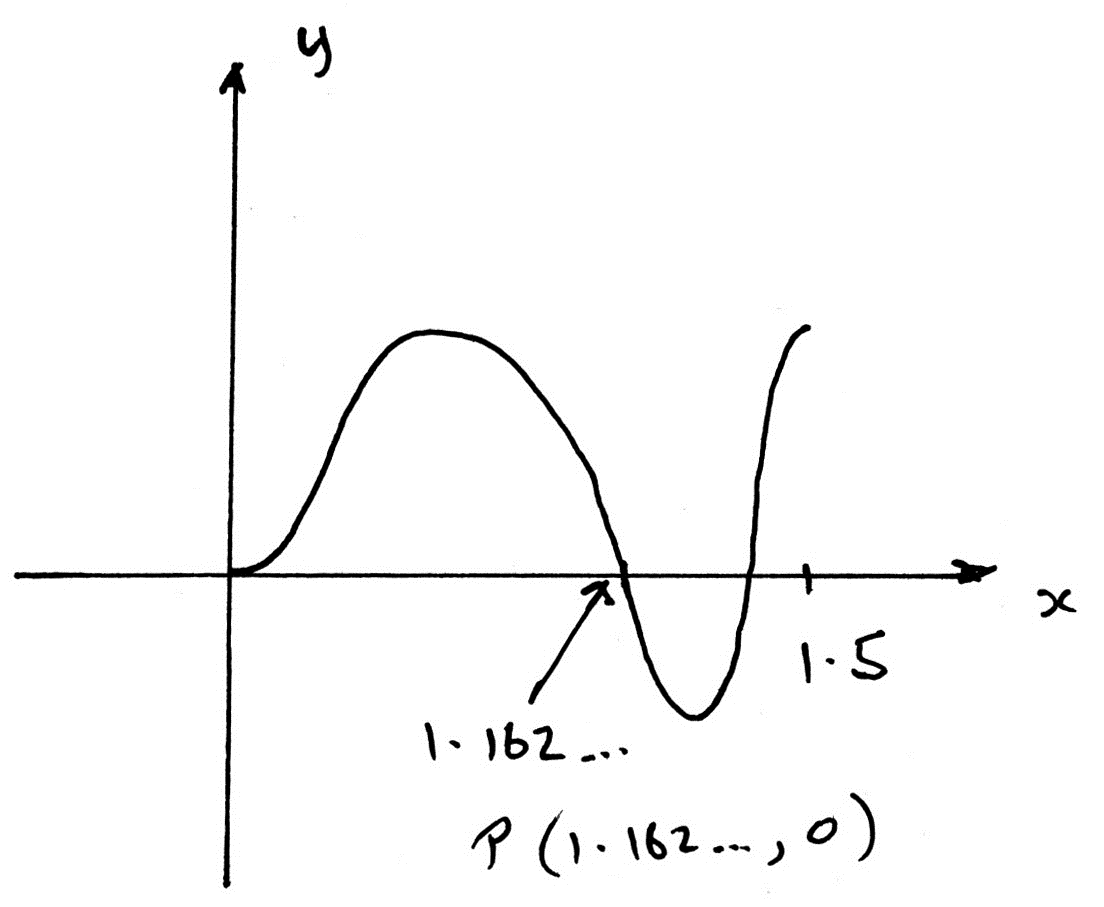 A1
A1
P is (1.16, 0) A1
Note: Award A1 for 1.16 seen anywhere, A1 for complete sketch.
Note: Allow FT on their answer from (b)
(ii) \(V = \int_0^{1.162…} {\pi {y^2}{\text{d}}x} \) M1A1
\( = 1.05\) A2
Note: Allow FT on their answers from (b) and (c)(i).
[6 marks]
Examiners report
Part A: Given that this question is at the easier end of the ‘proof by induction’ spectrum, it was disappointing that so many candidates failed to score full marks. The n = 1 case was generally well done. The whole point of the method is that it involves logic, so ‘let n = k’ or ‘put n = k’, instead of ‘assume … to be true for n = k’, gains no marks. The algebraic steps need to be more convincing than some candidates were able to show. It is astonishing that the R1 mark for the final statement was so often not awarded.
Part B: Part (a) was often well done, although some faltered after the first integration. Part (b) was also generally well done, although there were some errors with the constant of integration. In (c) the graph was often attempted, but errors in (b) usually led to manifestly incorrect plots. Many attempted the volume of integration and some obtained the correct value.
Question
Use the method of mathematical induction to prove that \({5^{2n}} – 24n – 1\) is divisible by 576 for \(n \in {\mathbb{Z}^ + }\).
▶️Answer/Explanation
Markscheme
\({\text{P}}(n):f(n) = {5^{2n}} – 24n – 1\) is divisible by 576 for \(n \in {\mathbb{Z}^ + }\)
for \(n = 1,{\text{ }}f(1) = {5^2} – 24 – 1 = 0\)
Zero is divisible by 576, (as every non-zero number divides zero), and so P(1) is true. R1
Note: Award R0 for P(1) = 0 shown and zero is divisible by 576 not specified.
Note: Ignore P(2) = 576 if P(1) = 0 is shown and zero is divisible by 576 is specified.
Assume \({\text{P}}(k)\) is true for some \(k{\text{ }}( \Rightarrow f(k) = N \times 576)\). M1
Note: Do not award M1 for statements such as “let n = k”.
consider \({\text{P}}(k + 1):f(k + 1) = {5^{2(k + 1)}} – 24(k + 1) – 1\) M1
\( = 25 \times {5^{2k}} – 24k – 25\) A1
EITHER
\( = 25 \times (24k + 1 + N \times 576) – 24k – 25\) A1
\( = 576k + 25 \times 576N\) which is a multiple of 576 A1
OR
\( = 25 \times {5^{2k}} – 600k – 25 + 600k – 24k\) A1
\( = 25({5^{2k}} – 24k – 1) + 576k\) (or equivalent) which is a multiple of 576 A1
THEN
P(1) is true and \({\text{P}}(k)\) true \( \Rightarrow {\text{P}}(k + 1)\) true, so \({\text{P}}(n)\) is true for all \(n \in {\mathbb{Z}^ + }\) R1
Note: Award R1 only if at least four prior marks have been awarded.
[7 marks]
Examiners report
This proof by mathematical induction challenged most candidates. While most candidates were able to show that P(1) = 0, a significant number did not state that zero is divisible by 576. A few candidates started their proof by looking at P(2). It was pleasing to see that the inductive step was reasonably well done by most candidates. However many candidates committed simple algebraic errors. The most common error was to state that \({5^{2(k + 1)}} = 5{(5)^{2k}}\). The concluding statement often omitted the required implication statement and also often omitted that P(1) was found to be true.
Question
(a) Use mathematical induction to prove that
\(\sum_{r=1}^{n}\frac{1}{(2r-1)(2r+1)}=\frac{n}{2n+1}, n\epsilon \mathbb{Z}^+.\)
(b) Hence show that the sum of the first (n + 1) terms of the series
\(\frac {1}{3}\frac {1}{15}+\frac{1}{35}+\frac {1}{63}+… is \frac {(n+1)}{(2n+3)}\)
▶️Answer/Explanation
Ans
(a) Let P(n) be the proposition \(\sum_{r=1}^{n}\frac{1}{(2r-1)(2r+1)}=\frac{n}{2n+1}\)
\(P(1):\sum_{1}^{1}\frac {1}{(2r-1)(2r+1)}=\frac {1}{3}=\frac {1}{2(1)+1}\) so P(1) is true
Assume that P(k) is true
\(P(k+1):\sum_{1}^{k+1}\frac {1}{(2r-1)(2r+1)}=\frac {k}{(2k+1)}+\frac {1}{(2k+1)(2k+3)}\)
=\(\frac {k(2k+3)+1}{(2k+1)(2k+3)}\)
=\(\frac {(k+1)(2k+1)}{(2k+1)(2k+3)}\)
=\(\frac {(k+1)}{(2k+1)+1}\)
Therefore P(1) is true and P(k) \(\Rightarrow P(k+1)\) so P(n) is true \(\forall n\epsilon \mathbb{Z}^+\)
(b) Checking that \(\frac {1}{3}+\frac {1}{15}+\frac {1}{35}\) is the same as \(\sum_{r=1}^{n}\frac {1}{(2r-1)(2r+1)}\)
(e.g. substitute r = 1,2)
Sum is therefore sum of (n+1) terms
i.e. \(\frac {(n+1)}{2(n+1)+1}\)
=\(\frac {n+1}{2n+3}\)
