Question 7. [Maximum mark: 13]
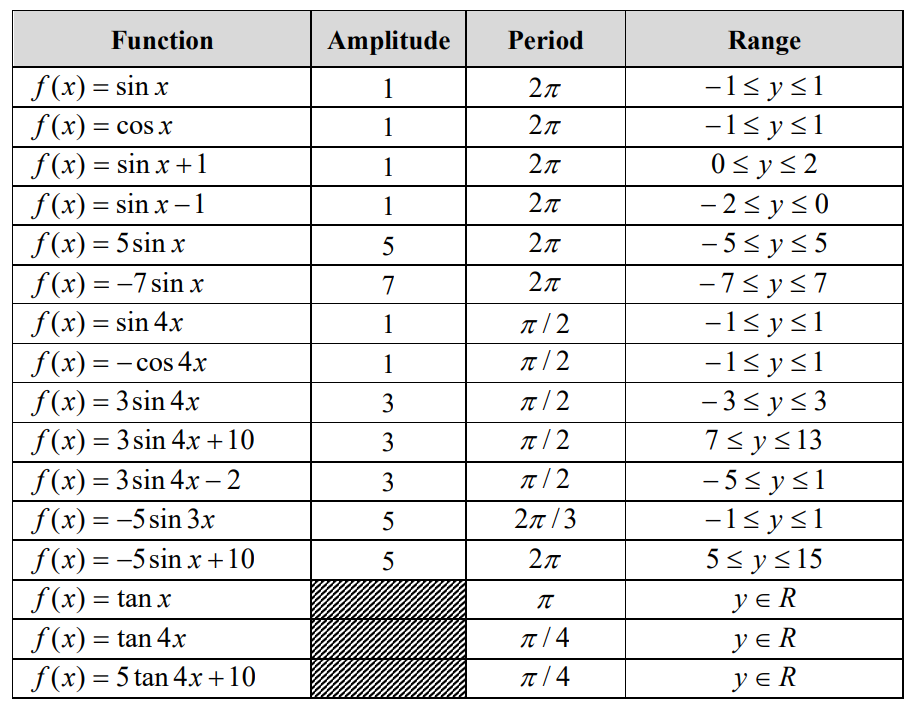
The six blades of a windmill rotate around a centre point C. Points A and B and the base of
the windmill are on level ground, as shown in the following diagram
From point A the angle of elevation of point C is 0.6 radians.
(a) Given that point A is 12 metres from the base of the windmill, find the height of point C above the ground. [2]
An observer walks 7 metres from point A to point B.
(b) Find the angle of elevation of point C from point B. [2]
The observer keeps walking until he is standing directly under point C. The observer has a height of 1.8 metres, and as the blades of the windmill rotate, the end of each blade passes 2.5 metres over his head.
(c) Find the length of each blade of the windmill. [2]
One of the blades is painted a different colour than the others. The end of this blade is labelled point D. The height h , in metres, of point D above the ground can be modelled by the function \(h\left ( t \right )=p\cos \left ( \frac{3\pi }{10}t \right )=q\) , where t is in seconds and \(p,q\epsilon R\) When t = 0, point D is at its maximum height.
(d) Find the value of p and the value of q. [4]
If the observer stands directly under point C for one minute, point D will pass over his
head n times.
(e) Find the value of n .
Answer/Explanation
(a) \(\tan 0.6=\frac{h}{12}\)
8.20964…
8.21(m)
(b)
\(\tan B=\frac{8.2096..}{5}\) OR \(\tan ^{-1}1.6419\)
1.02375
1.02(radians) ( accept \(58.7^{\circ}\)
(c)\( x+1.8+2.5=8.20964….\) ( or equivalent )
3.90964..
3.91(m)
(d) METHOD 1
recognition that blade length =amplitude , \(p=\frac{max-min}{2}\) p=3.91
centre of windmill =vertical shift ,\(q=\frac{max+min}{2}\)
q=8.21
METHOD 2
attempting to form two equations in terms of p and q
\(12.1192…=p\cos \left ( \frac{3\pi }{10} .0\right )+q\), \(4.3000…=p\cos \left ( \frac{3\pi }{10} .\frac{10}{3}\right )+q\)
(e) appropriate working towards finding the period
period =\(\frac{2\pi }{\frac{3\pi }{10}}\) (=6.6666…)
rotations per minute =\(\frac{60}{their period }\)
n=9(must be an integer )(accept n=10,n=18,n=19)
Question: [Maximum mark: 12]
A scientist conducted a nine-week experiment on two plants, A and B, of the same species. He wanted to determine the effect of using a new plant fertilizer. Plant A was given fertilizer
regularly, while Plant B was not.
The scientist found that the height of Plant A, hA cm, at time t weeks can be modelled by the function hA (t) = sin(2t + 6) + 9t + 27, where 0 ≤ t ≤ 9.
The scientist found that the height of Plant B, hB cm, at time t weeks can be modelled by the function hB (t) = 8t + 32, where 0 ≤ t ≤ 9.
(a) Use the scientist’s models to find the initial height of
(i) Plant B;
(ii) Plant A correct to three significant figures.
(b) Find the values of t when hA (t) = hB (t).
(c) For 0 ≤ t ≤ 9, find the total amount of time when the rate of growth of Plant B was greater than the rate of growth of Plant A.
Answer/Explanation
Ans:
(a) (i) 32 (cm)
(ii) hA (0) = sin (6) + 27
= 26.7205…
= 26.7 (cm)
(b) attempts to solve hA (t) = hB (t) for t
t = 4.00746…,4.70343…,5.88332…
t = 4.01,4.70,5.88 (weeks)
(c) recognises that hA‘ (t) and hB‘ (t) are required
attempts to solve hA‘ (t) = hB‘ (t) for t
t =1.18879… and 2.23598… OR 4.33038… and 5.37758… OR 7.47197… and 8.51917…
Question
The following diagram shows a water wheel with center O and radius 10 meters. Water flows into buckets, turning the wheel clockwise at a constant speed.
The height, h meters, of the top of a bucket above the ground t seconds after it passes through point A is modelled by the function
h (t) = 13 + 8 cos\((\frac{\pi }{18}t)-6sin(\frac{\pi }{18}t)\) , for t ≥ 0.
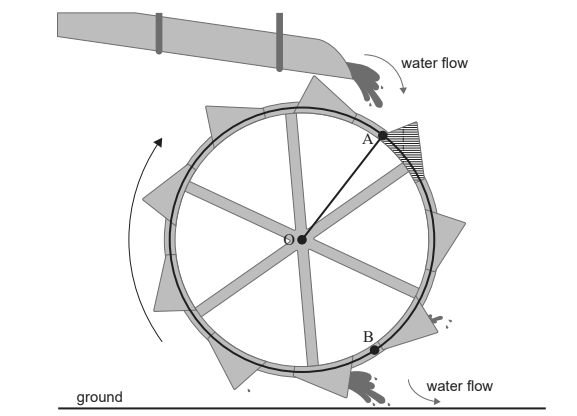
(a)(i) Find the height of point A above the ground.
(ii) Calculate the number of seconds it takes for the water wheel to complete one rotation.
(iii) Hence find the number of rotations the water wheel makes in one hour. [6]
A bucket moves around to point B which is at a height of 4.06 meters above the ground.
It takes k seconds for the top of this bucket to go from point A to point B.
(b) Find k . [3]
The chord [AB] is 17.0 meters, correct to three significant figures.
(c) Find AÔB. [3]
(d) Determine the rate of change of h when the top of the bucket is at B. [2]
Answer/Explanation
Ans



2.03197, 116.4230
2.03 (1160)

Question
The following graph shows the depth of water, y metres , at a point P, during one day. The time t is given in hours, from midnight to noon.
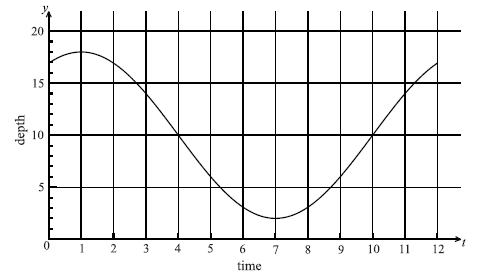
Use the graph to write down an estimate of the value of t when
(i) the depth of water is minimum;
(ii) the depth of water is maximum;
(iii) the depth of the water is increasing most rapidly.
The depth of water can be modelled by the function \(y = \cos A(B(t – 1)) + C\) .
(i) Show that \(A = 8\) .
(ii) Write down the value of C.
(iii) Find the value of B.
A sailor knows that he cannot sail past P when the depth of the water is less than 12 m . Calculate the values of t between which he cannot sail past P.
Answer/Explanation
Markscheme
(i) 7 A1 N1
(ii) 1 A1 N1
(iii) 10 A1 N1
[3 marks]
(i) evidence of appropriate approach M1
e.g. \(A = \frac{{18 – 2}}{2}\)
\(A = 8\) AG N0
(ii) \(C = 10\) A2 N2
(iii) METHOD 1
\({\text{period}} = 12\) (A1)
evidence of using \(B \times {\rm{period}} = 2\pi \) (accept \(360^\circ \) ) (M1)
e.g. \(12 = \frac{{2\pi }}{B}\)
\(B = \frac{\pi }{6}\) (accept 0.524 or 30) A1 N3
METHOD 2
evidence of substituting (M1)
e.g. \(10 = 8\cos 3B + 10\)
simplifying (A1)
e.g. \(\cos 3B = 0\) \(\left( {3B = \frac{\pi }{2}} \right)\)
\(B = \frac{\pi }{6}\) (accept 0.524 or 30) A1 N3
[6 marks]
correct answers A1A1
e.g. \(t = 3.52\) , \(t = 10.5\) , between 03:31 and 10:29 (accept 10:30) N2
[2 marks]
Question
[Maximum mark: 14] [without GDC]
Complete the following table
Answer/Explanation
Ans: