Question
Two fair 4-sided dice, one red and one green, are thrown. For each die, the faces are labelled 1, 2, 3, 4. The score for each die is the number which lands face down.
List the pairs of scores that give a sum of 6.[3]
The probability distribution for the sum of the scores on the two dice is shown below.

Find the value of p , of q , and of r .[3]
Fred plays a game. He throws two fair 4-sided dice four times. He wins a prize if the sum is 5 on three or more throws.
Find the probability that Fred wins a prize.[6]
Answer/Explanation
Markscheme
three correct pairs A1A1A1 N3
e.g. (2, 4), (3, 3), (4, 2) , R2G4, R3G3, R4G2
[3 marks]
\(p = \frac{1}{{16}}\) , \(q = \frac{2}{{16}}\) , \(r = \frac{2}{{16}}\) A1A1A1 N3
[3 marks]
let X be the number of times the sum of the dice is 5
evidence of valid approach (M1)
e.g. \(X \sim {\rm{B}}(n{\text{, }}p)\) , tree diagram, 5 sets of outcomes produce a win
one correct parameter (A1)
e.g. \(n = 4\) , \(p = 0.25\) , \(q = 0.75\)
Fred wins prize is \({\rm{P}}(X \ge 3)\) (A1)
appropriate approach to find probability M1
e.g. complement, summing probabilities, using a CDF function
correct substitution (A1)
e.g. \(1 – 0.949 \ldots \) , \(1 – \frac{{243}}{{256}}\) , \(0.046875 + 0.00390625\) , \(\frac{{12}}{{256}} + \frac{1}{{256}}\)
\({\text{probability of winning}} = 0.0508\) \(\left( {\frac{{13}}{{256}}} \right)\) A1 N3
[6 marks]
Question
A bag contains four gold balls and six silver balls.
Two balls are drawn at random from the bag, with replacement. Let \(X\) be the number of gold balls drawn from the bag.
Fourteen balls are drawn from the bag, with replacement.
(i) Find \({\rm{P}}(X = 0)\) .
(ii) Find \({\rm{P}}(X = 1)\) .
(iii) Hence, find \({\rm{E}}(X)\) .
Hence, find \({\rm{E}}(X)\) .
Find the probability that exactly five of the balls are gold.
Find the probability that at most five of the balls are gold.
Given that at most five of the balls are gold, find the probability that exactly five of the balls are gold. Give the answer correct to two decimal places.
Answer/Explanation
Markscheme
METHOD 1
(i) appropriate approach (M1)
eg \(\frac{6}{{10}} \times \frac{6}{{10}}\) , \(\frac{6}{{10}} \times \frac{5}{9}\) , \(\frac{6}{{10}} \times \frac{5}{{10}}\)
\({\rm{P}}(X = 0) = \frac{9}{{25}} = 0.36\) A1 N2
(ii) multiplying one pair of gold and silver probabilities (M1)
eg \(\frac{6}{{10}} \times \frac{4}{{10}}\) , \(\frac{6}{{10}} \times \frac{4}{9}\) , 0.24
adding the product of both pairs of gold and silver probabilities (M1)
eg \(\frac{6}{{10}} \times \frac{4}{{10}} \times 2\) , \(\frac{6}{{10}} \times \frac{4}{9} + \frac{4}{{10}} \times \frac{6}{9}\)
\({\rm{P}}(X = 1) = \frac{{12}}{{25}} = 0.48\) A1 N3
(iii)
\({\rm{P}}(X = 2) = 0.16\) (seen anywhere) (A1)
correct substitution into formula for \({\rm{E}}(X)\) (A1)
eg \(0 \times 0.36 + 1 \times 0.48 + 2 \times 0.16\) , \(0.48 + 0.32\)
\({\rm{E}}(X) = \frac{4}{5} = 0.8\) A1 N3
METHOD 2
(i) evidence of recognizing binomial (may be seen in part (ii)) (M1)
eg \(X \sim {\rm{B}}(2,0.6)\) , \(\left( \begin{array}{l}
2\\
0
\end{array} \right){(0.4)^2}{(0.6)^0}\)
correct probability for use in binomial (A1)
eg \(p = 0.4\) , \(X \sim {\rm{B}}(2,0.4)\) , \(^2{C_0}{(0.4)^0}{(0.6)^2}\)
\({\rm{P}}(X = 0) = \frac{9}{{25}} = 0.36\) A1 N3
(ii) correct set up (A1)
eg \(_2{C_1}{(0.4)^1}{(0.6)^1}\)
\({\rm{P}}(X = 1) = \frac{{12}}{{25}} = 0.48\) A1 N2
(iii)
attempt to substitute into \(np\) (M1)
eg \(2 \times 0.6\)
correct substitution into \(np\) (A1)
eg \(2 \times 0.4\)
\({\rm{E}}(X) = \frac{4}{5} = 0.8\) A1 N3
[8 marks]
METHOD 1
\({\rm{P}}(X = 2) = 0.16\) (seen anywhere) (A1)
correct substitution into formula for \({\rm{E}}(X)\) (A1)
eg \(0 \times 0.36 + 1 \times 0.48 + 2 \times 0.16\) , \(0.48 + 0.32\)
\({\rm{E}}(X) = \frac{4}{5} = 0.8\) A1 N3
METHOD 2
attempt to substitute into \(np\) (M1)
eg \(2 \times 0.6\)
correct substitution into \(np\) (A1)
eg \(2 \times 0.4\)
\({\rm{E}}(X) = \frac{4}{5} = 0.8\) A1 N3
[3 marks]
Let \(Y\) be the number of gold balls drawn from the bag.
evidence of recognizing binomial (seen anywhere) (M1)
eg \(_{14}{C_5}{(0.4)^5}{(0.6)^9}\) , \({\rm{B}}(14,0.4)\)
\({\rm{P}}(Y = 5) = 0.207\) A1 N2
[2 marks]
recognize need to find \({\rm{P}}(Y \le 5)\) (M1)
\({\rm{P}}(Y \le 5) = 0.486\) A1 N2
[2 marks]
Let \(Y\) be the number of gold balls drawn from the bag.
recognizing conditional probability (M1)
eg \({\rm{P}}(A|B)\) , \({\rm{P}}(Y = 5|Y \le 5)\) , \(\frac{{{\rm{P}}(Y = 5)}}{{{\rm{P}}(Y \le 5)}}\) , \(\frac{{0.207}}{{0.486}}\)
\({\rm{P}}(Y = 5|Y \le 5) = 0.42522518\) (A1)
\({\rm{P}}(Y = 5|Y \le 5) = 0.43\) (to \(2\) dp) A1 N2
[3 marks]
Question
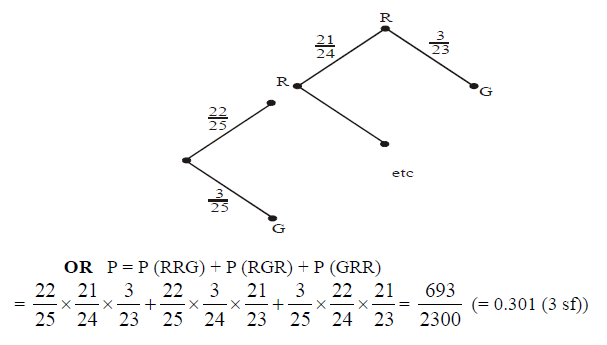
A box contains 22 red apples and 3 green apples. Three apples are selected at
random, one after the other, without replacement.
(a) The first two apples are green. What is the probability that the third apple is red?
(b) What is the probability that exactly two of the three apples are red? [Maximum mark: 6] [with GDC]
Answer/Explanation
Ans.
(a) P = \(\frac{22}{23}(=0.957(3\;sf))\)
(b)
Question
A bag contains 10 red balls, 10 green balls and 6 white balls. Two balls are drawn at random from the bag without replacement. What is the probability that they are of different colours? [Maximum mark: 4] [with GDC]
Answer/Explanation
Ans.
P(different colours) = 1 – [P(GG) + P(RR) + P(WW)]
=\( 1-\left ( \frac{10}{6}x\frac{9}{25}+\frac{10}{26}x\frac{9}{25}+\frac{6}{26}x\frac{5}{25} \right )=1-\left ( \frac{210}{650} \right )=\frac{44}{65}(=0.677,to\;3\;sf)\)
OR
P(different colours) = P(GR) + P(RG) + P(GW) + P(WG) + P(RW) + P(WR)
=\(4\left ( \frac{10}{26}x\frac{6}{25} \right )+2\left ( \frac{10}{26}x\frac{10}{25} \right )=\frac{44}{65}(=0.677,to\;3\;sf)\)
Question
Dumisani is a student at IB World College. The probability that he will be woken by his
alarm clock is \(\frac{7}{8}\). If he is woken by his alarm clock the probability he will be late for
school is \(\frac{1}{4}\) . If he is not woken by his alarm clock the probability he will be late for school is \(\frac{3}{5}\) .
Let W be the event “Dumisani is woken by his alarm clock”.
Let L be the event “Dumisani is late for school”.
(a) Copy and complete the tree diagram below.

(b) Calculate the probability that Dumisani will be late for school.
(c) Given that Dumisani is late for school what is the probability that he was woken by his alarm clock? [Maximum mark: 11] [with GDC]
Answer/Explanation
Ans.
(a)
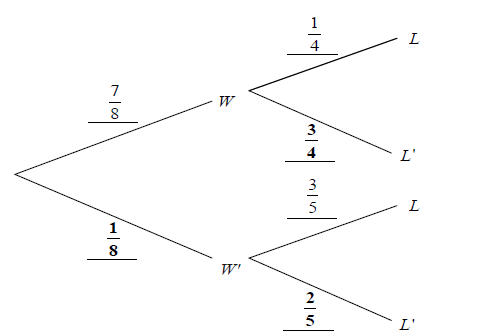
(b) Probability that he will be late is \(\frac{7}{8}x\frac{1}{4}+\frac{1}{8}x\frac{3}{5}=\frac{47}{160}(0.294)\)
(c) P(W │L) = \(\frac{\frac{7}{8}x\frac{1}{4}}{\frac{47}{160}}=\frac{\frac{7}{32}}{\frac{47}{160}}=\frac{35}{47}(=0.745)\)
Question
In a school of 88 boys, 32 study economics (E), 28 study history (H) and 39 do not
study either subject. This information is represented in the following Venn diagram.

(a) Calculate the values a,b, c .
(b) A student is selected at random.
(i) Calculate the probability that he studies both economics and history.
(ii) Given that he studies economics, calculate the probability that he does not study history.
(c) A group of three students is selected at random from the school.
(i) Calculate the probability that none of these students studies economics.
(ii) Calculate the probability that at least one of these students studies economics. [Maximum mark: 12] [with GDC]
Answer/Explanation
Ans.
(a)
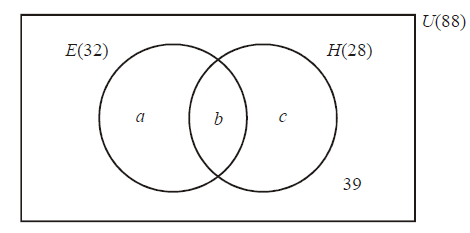
n (E ∪ H) = a + b + c = 88 – 39 = 49
n (E ∪ H) = 32 + 28 – b = 49 ⇔ b = 11
a = 32 – 11 = 21
c = 28 – 11 = 17
(b) (i) P(E ∩ H) = \(\frac{11}{88}=\frac{1}{8}\)
(ii) P(H′│E) =\(\frac{P({H}’\cap E)}{P(E)}=\frac{\frac{21}{88}}{\frac{32}{88}}=\frac{21}{32}(=0.656)\) Or directly = \(\frac{21}{32}\)
(c) (i) P(none in economics) = \(\frac{56x55x54}{88x87x86}=0.253\)
(ii) P(at least one) = 1 – 0.253= 0.747
OR
\(3\left ( \frac{32}{88}x\frac{56}{87}x\frac{55}{86} \right )+3\left ( \frac{32}{88}x\frac{31}{87}x\frac{56}{86} \right )+\frac{32}{88}x\frac{31}{87}x\frac{30}{86}=0.747\)
Question
Two restaurants, Center and New, sell fish rolls and salads.
Let F be the event a customer chooses a fish roll.
Let S be the event a customer chooses a salad.
Let N be the event a customer chooses neither a fish roll nor a salad.
In the Center restaurant P(F) = 0.31, P(S) = 0.62 , P(N) = 0.14 .
(a) Show that P(F ∩ S) = 0.07 .
(b) Given that a customer chooses a salad, find the probability the customer also chooses a fish roll.
(c) Are F and S independent events? Justify your answer.
At New restaurant, P(N) = 0.14 . Twice as many customers choose a salad as choose a fish roll. Choosing a fish roll is independent of choosing a salad.
(d) Find the probability that a fish roll is chosen. [Maximum mark: 16] [with GDC]
Answer/Explanation
Ans.
(a) P(F ∪ S) = 1 – 0.14 (= 0.86)
P(F ∩ S) = 0.93 – 0.86= 0.07
Note: You can use Venn Diagram
(b) P(F │ S) \(\left ( =\frac{P(F\cap S)}{P(S)} \right )=\frac{0.07}{0.62}=0.113\)
(c) F and S are not independent
EITHER
If independent P(F │ S) = P(F), 0.113 ≠ 0.31
OR
If independent P(F ∩ S) = P(F) P(S), 0.07 ≠ 0.31 x 0.62 (= 0.1922)
(d) Let P(F) = x
P(S) = 2P(F) = 2x
P(F ∪ S) = P(F)P(S) – P(F)P(S) ⇔ 0.86 = x + 2x – 2x2 ⇔ 2x2 – 3x + 0.86 = 0
x = 0.386, x = 1.11
P(F) = 0.386
Question
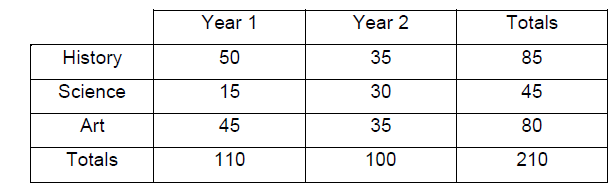
The table below shows the subjects studied by 210 students at a college.
(a) A student from the college is selected at random.
Let A be the event the student studies Art.
Let B be the event the student is in Year 2.
(i) Find P(A) .
(ii) Find the probability that the student is a Year 2 Art student.
(iii) Are the events A and B independent? Justify your answer.
(b) Given that a History student is selected at random, calculate the probability that
the student is in Year 1.
(c) Two students are selected at random from the college. Calculate the probability that one student is in Year 1, and the other in Year 2. [Maximum mark: 12] [with GDC]
Answer/Explanation
Ans.
(a) (i) P(A)=\(\frac{80}{210}=\left ( \frac{8}{21}=0.381 \right )\)
(ii) P(year 2 art) = \(\frac{35}{210}=\left ( \frac{1}{6}=0.167 \right )\)
(iii) No (the events are not independent
EITHER P(A∩B) = P(A) x P(B) (to be independent)
P(B) = \(\frac{100}{210}\left ( =\frac{10}{21}=0.476 \right )\) but \(\frac{1}{6}\neq \frac{8}{21}x\frac{10}{21}\)
OR P(A)=P(A │ B) (to be independent)
P( A │ B) =\(\frac{35}{100}\) but \(\frac{8}{21}\neq \frac{35}{100}\)
OR P(B)=P(B │ A) (to be independent)
P(B) = \(\frac{100}{210}\left ( =\frac{10}{21}=0.476 \right ),\) P(B │ A) = \(\frac{35}{80}\) but \(\frac{35}{80}\neq \frac{100}{210}\)
(b) n (history) = 85
P(year 1 │ history) = \(\frac{50}{85}=\left ( \frac{10}{17}=0.588 \right )\)
(c) \(\left ( \frac{110}{210}x\frac{100}{209} \right )+\left ( \frac{100}{210}x\frac{110}{209} \right )\left ( =2x\frac{110}{210}x\frac{100}{209} \right )=\frac{200}{399}(=0.501)\)
Question
In a class of 100 boys, 55 boys play football and 75 boys play rugby. Each boy must
play at least one sport from football and rugby.
(a) (i) Find the number of boys who play both sports.
(ii) Write down the number of boys who play only rugby.
(b) One boy is selected at random.
(i) Find the probability that he plays only one sport.
(ii) Given that the boy selected plays only one sport, find the probability that he
plays rugby.
Let A be the event that a boy plays football and B be the event that a boy plays rugby.
(c) Explain why A and B are not mutually exclusive.
(d) Show that A and B are not independent. [Maximum mark: 12] [with GDC]
Answer/Explanation
Ans.
(a) (i) Venn diagram, 30
(ii) 45
(b) (i) \(\frac{70}{100}\left ( =\frac{7}{10} \right )\)
(ii) \(\frac{45}{70}\left ( =\frac{9}{14} \right )\)
(c) P(A ∩ B) = 0.3 ≠ 0
(d) P(A ∩ B) ≠ P(A) × P(B), \(\frac{30}{100}\neq \frac{75}{100}x\frac{55}{100},\frac{30}{55}\neq \frac{75}{100}\)
OR P(B│A) ≠ P(B), \(\frac{30}{55}\neq \frac{75}{100}\)
Question
In a group of 16 students, 12 take art and 8 take music. One student takes neither art
nor music. The Venn diagram below shows the events art and music. The values p , q ,
r and s represent numbers of students.
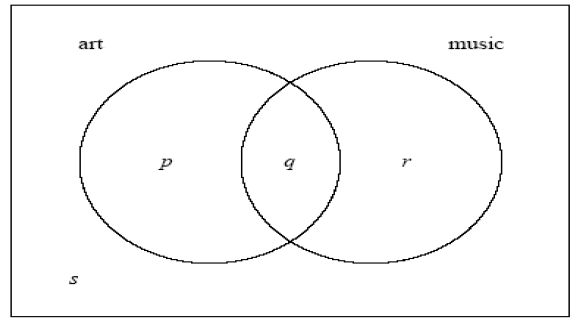
(a) (i) Write down the value of s .
(ii) Find the value of q .
(iii) Write down the value of p and of r .
(b) (i) A student is selected at random. Given that the student takes music, write
down the probability the student takes art.
(ii) Hence, show that taking music and taking art are not independent events.
(c) Two students are selected at random, one after the other. Find the probability that the first student takes only music and the second student takes only art. [Maximum mark: 13] [with GDC]
Answer/Explanation
Ans.
(a) (i) s = 1
(ii) q = 5
(iii) p = 7, r = 3
(b) (i) P(art|music) = \(\frac{5}{8}\)
(ii) METHOD 1
P(art)=\(\frac{12}{16}\left ( =\frac{3}{4} \right )\) \( \frac{3}{4}\neq \frac{5}{8}\) the events are not independent
METHOD 2
P(art) × P(music) = \(\frac{96}{256}\left ( =\frac{3}{8} \right ) \) \(\frac{12}{16}x\frac{8}{16}\neq \frac{5}{16}\) the events are not independent
(c) P(first takes only music) = \(\frac{3}{16}\)
P(second takes only art)= \(\frac{7}{15}\)
P(music and art)= \(\frac{3}{16}x\frac{7}{15}=\frac{21}{240}\left ( =\frac{7}{80} \right )\)
Question
A box contains 22 red apples and 3 green apples. Three apples are selected at
random, one after the other, without replacement.
(a) The first two apples are green. What is the probability that the third apple is red?
(b) What is the probability that exactly two of the three apples are red? [Maximum mark: 6] [with GDC]
Answer/Explanation
Ans.
(a) P = \(\frac{22}{23}(=0.957(3\;sf))\)
(b)

Question
A bag contains 10 red balls, 10 green balls and 6 white balls. Two balls are drawn at random from the bag without replacement. What is the probability that they are of different colours? [Maximum mark: 4] [with GDC]
Answer/Explanation
Ans.
P(different colours) = 1 – [P(GG) + P(RR) + P(WW)]
=\( 1-\left ( \frac{10}{6}x\frac{9}{25}+\frac{10}{26}x\frac{9}{25}+\frac{6}{26}x\frac{5}{25} \right )=1-\left ( \frac{210}{650} \right )=\frac{44}{65}(=0.677,to\;3\;sf)\)
OR
P(different colours) = P(GR) + P(RG) + P(GW) + P(WG) + P(RW) + P(WR)
=\(4\left ( \frac{10}{26}x\frac{6}{25} \right )+2\left ( \frac{10}{26}x\frac{10}{25} \right )=\frac{44}{65}(=0.677,to\;3\;sf)\)
Question
Dumisani is a student at IB World College. The probability that he will be woken by his
alarm clock is \(\frac{7}{8}\). If he is woken by his alarm clock the probability he will be late for
school is \(\frac{1}{4}\) . If he is not woken by his alarm clock the probability he will be late for school is \(\frac{3}{5}\) .
Let W be the event “Dumisani is woken by his alarm clock”.
Let L be the event “Dumisani is late for school”.
(a) Copy and complete the tree diagram below.

(b) Calculate the probability that Dumisani will be late for school.
(c) Given that Dumisani is late for school what is the probability that he was woken by his alarm clock? [Maximum mark: 11] [with GDC]
Answer/Explanation
Ans.
(a)

(b) Probability that he will be late is \(\frac{7}{8}x\frac{1}{4}+\frac{1}{8}x\frac{3}{5}=\frac{47}{160}(0.294)\)
(c) P(W │L) = \(\frac{\frac{7}{8}x\frac{1}{4}}{\frac{47}{160}}=\frac{\frac{7}{32}}{\frac{47}{160}}=\frac{35}{47}(=0.745)\)
Question
In a school of 88 boys, 32 study economics (E), 28 study history (H) and 39 do not
study either subject. This information is represented in the following Venn diagram.

(a) Calculate the values a,b, c .
(b) A student is selected at random.
(i) Calculate the probability that he studies both economics and history.
(ii) Given that he studies economics, calculate the probability that he does not study history.
(c) A group of three students is selected at random from the school.
(i) Calculate the probability that none of these students studies economics.
(ii) Calculate the probability that at least one of these students studies economics. [Maximum mark: 12] [with GDC]
Answer/Explanation
Ans.
(a)

n (E ∪ H) = a + b + c = 88 – 39 = 49
n (E ∪ H) = 32 + 28 – b = 49 ⇔ b = 11
a = 32 – 11 = 21
c = 28 – 11 = 17
(b) (i) P(E ∩ H) = \(\frac{11}{88}=\frac{1}{8}\)
(ii) P(H′│E) =\(\frac{P({H}’\cap E)}{P(E)}=\frac{\frac{21}{88}}{\frac{32}{88}}=\frac{21}{32}(=0.656)\) Or directly = \(\frac{21}{32}\)
(c) (i) P(none in economics) = \(\frac{56x55x54}{88x87x86}=0.253\)
(ii) P(at least one) = 1 – 0.253= 0.747
OR
\(3\left ( \frac{32}{88}x\frac{56}{87}x\frac{55}{86} \right )+3\left ( \frac{32}{88}x\frac{31}{87}x\frac{56}{86} \right )+\frac{32}{88}x\frac{31}{87}x\frac{30}{86}=0.747\)
Question
Two restaurants, Center and New, sell fish rolls and salads.
Let F be the event a customer chooses a fish roll.
Let S be the event a customer chooses a salad.
Let N be the event a customer chooses neither a fish roll nor a salad.
In the Center restaurant P(F) = 0.31, P(S) = 0.62 , P(N) = 0.14 .
(a) Show that P(F ∩ S) = 0.07 .
(b) Given that a customer chooses a salad, find the probability the customer also chooses a fish roll.
(c) Are F and S independent events? Justify your answer.
At New restaurant, P(N) = 0.14 . Twice as many customers choose a salad as choose a fish roll. Choosing a fish roll is independent of choosing a salad.
(d) Find the probability that a fish roll is chosen. [Maximum mark: 16] [with GDC]
Answer/Explanation
Ans.
(a) P(F ∪ S) = 1 – 0.14 (= 0.86)
P(F ∩ S) = 0.93 – 0.86= 0.07
Note: You can use Venn Diagram
(b) P(F │ S) \(\left ( =\frac{P(F\cap S)}{P(S)} \right )=\frac{0.07}{0.62}=0.113\)
(c) F and S are not independent
EITHER
If independent P(F │ S) = P(F), 0.113 ≠ 0.31
OR
If independent P(F ∩ S) = P(F) P(S), 0.07 ≠ 0.31 x 0.62 (= 0.1922)
(d) Let P(F) = x
P(S) = 2P(F) = 2x
P(F ∪ S) = P(F)P(S) – P(F)P(S) ⇔ 0.86 = x + 2x – 2x2 ⇔ 2x2 – 3x + 0.86 = 0
x = 0.386, x = 1.11
P(F) = 0.386
Question
The table below shows the subjects studied by 210 students at a college.

(a) A student from the college is selected at random.
Let A be the event the student studies Art.
Let B be the event the student is in Year 2.
(i) Find P(A) .
(ii) Find the probability that the student is a Year 2 Art student.
(iii) Are the events A and B independent? Justify your answer.
(b) Given that a History student is selected at random, calculate the probability that
the student is in Year 1.
(c) Two students are selected at random from the college. Calculate the probability that one student is in Year 1, and the other in Year 2. [Maximum mark: 12] [with GDC]
Answer/Explanation
Ans.
(a) (i) P(A)=\(\frac{80}{210}=\left ( \frac{8}{21}=0.381 \right )\)
(ii) P(year 2 art) = \(\frac{35}{210}=\left ( \frac{1}{6}=0.167 \right )\)
(iii) No (the events are not independent
EITHER P(A∩B) = P(A) x P(B) (to be independent)
P(B) = \(\frac{100}{210}\left ( =\frac{10}{21}=0.476 \right )\) but \(\frac{1}{6}\neq \frac{8}{21}x\frac{10}{21}\)
OR P(A)=P(A │ B) (to be independent)
P( A │ B) =\(\frac{35}{100}\) but \(\frac{8}{21}\neq \frac{35}{100}\)
OR P(B)=P(B │ A) (to be independent)
P(B) = \(\frac{100}{210}\left ( =\frac{10}{21}=0.476 \right ),\) P(B │ A) = \(\frac{35}{80}\) but \(\frac{35}{80}\neq \frac{100}{210}\)
(b) n (history) = 85
P(year 1 │ history) = \(\frac{50}{85}=\left ( \frac{10}{17}=0.588 \right )\)
(c) \(\left ( \frac{110}{210}x\frac{100}{209} \right )+\left ( \frac{100}{210}x\frac{110}{209} \right )\left ( =2x\frac{110}{210}x\frac{100}{209} \right )=\frac{200}{399}(=0.501)\)
Question
In a class of 100 boys, 55 boys play football and 75 boys play rugby. Each boy must
play at least one sport from football and rugby.
(a) (i) Find the number of boys who play both sports.
(ii) Write down the number of boys who play only rugby.
(b) One boy is selected at random.
(i) Find the probability that he plays only one sport.
(ii) Given that the boy selected plays only one sport, find the probability that he
plays rugby.
Let A be the event that a boy plays football and B be the event that a boy plays rugby.
(c) Explain why A and B are not mutually exclusive.
(d) Show that A and B are not independent. [Maximum mark: 12] [with GDC]
Answer/Explanation
Ans.
(a) (i) Venn diagram, 30
(ii) 45
(b) (i) \(\frac{70}{100}\left ( =\frac{7}{10} \right )\)
(ii) \(\frac{45}{70}\left ( =\frac{9}{14} \right )\)
(c) P(A ∩ B) = 0.3 ≠ 0
(d) P(A ∩ B) ≠ P(A) × P(B), \(\frac{30}{100}\neq \frac{75}{100}x\frac{55}{100},\frac{30}{55}\neq \frac{75}{100}\)
OR P(B│A) ≠ P(B), \(\frac{30}{55}\neq \frac{75}{100}\)
Question
In a group of 16 students, 12 take art and 8 take music. One student takes neither art
nor music. The Venn diagram below shows the events art and music. The values p , q ,
r and s represent numbers of students.

(a) (i) Write down the value of s .
(ii) Find the value of q .
(iii) Write down the value of p and of r .
(b) (i) A student is selected at random. Given that the student takes music, write
down the probability the student takes art.
(ii) Hence, show that taking music and taking art are not independent events.
(c) Two students are selected at random, one after the other. Find the probability that the first student takes only music and the second student takes only art. [Maximum mark: 13] [with GDC]
Answer/Explanation
Ans.
(a) (i) s = 1
(ii) q = 5
(iii) p = 7, r = 3
(b) (i) P(art|music) = \(\frac{5}{8}\)
(ii) METHOD 1
P(art)=\(\frac{12}{16}\left ( =\frac{3}{4} \right )\) \( \frac{3}{4}\neq \frac{5}{8}\) the events are not independent
METHOD 2
P(art) × P(music) = \(\frac{96}{256}\left ( =\frac{3}{8} \right ) \) \(\frac{12}{16}x\frac{8}{16}\neq \frac{5}{16}\) the events are not independent
(c) P(first takes only music) = \(\frac{3}{16}\)
P(second takes only art)= \(\frac{7}{15}\)
P(music and art)= \(\frac{3}{16}x\frac{7}{15}=\frac{21}{240}\left ( =\frac{7}{80} \right )\)
Question: [Maximum mark: 6]
A discrete random variable, X, has the following probability distribution:
| x | 0 | 1 | 2 | 3 |
| P(X=x) | 0.41 | k – 0.28 | 0.46 | 0.29-2k2 |
(a) Show that 2k2 – k + 0.12 = 0.
(b) Find the value of k , giving a reason for your answer.
(c) Hence, find E(X).
Answer/Explanation
Ans:
(a) 0.41 + k – 0.28 + 0.46 + 0.29 – 2k2 = 1 OR k – 2k2 + 0.01 = 0.13 (or equivalent)
2k2 – k + 0.12 = 0
(b) one of 0.2 OR 0.3
k = 0.3
reasoning to reject k = 0.2 eg P(1) = k-0.28 ≥ 0 therefore k ≠ 0.2
(c) attempting to use the expected value formula
E(X) = 0 × 0.41 + 1 × (0.3-0.28)+2 × 0.46+3 × (0.29-2 × 0.32)
= 1.27
Note: Award M1A0 if additional values are given.
