Question
A bakery makes two types of muffins: chocolate muffins and banana muffins.
The weights, C grams, of the chocolate muffins are normally distributed with a mean of 62g and standard deviation of 2.9g.
(a) Find the probability that a randomly selected chocolate muffin weighs less than 61g.
(b) In a random selection of 12 chocolate muffins, find the probability that exactly 5 weigh less than 61g.
The weights, B grams, of the banana muffins are normally distributed with a mean of 68 g and standard deviation of 3.4g.
Each day 60% of the muffins made are chocolate.
On a particular day, a muffin is randomly selected from all those made at the bakery.
(c) (i) Find the probability that the randomly selected muffin weighs less than 61 g .
(ii) Given that a randomly selected muffin weighs less than 61g, find the probability that it is chocolate.
The machine that makes the chocolate muffins is adjusted so that the mean weight of the chocolate muffins remains the same but their standard deviation changes to σ g. The machine that makes the banana muffins is not adjusted. The probability that the weight of a randomly selected muffin from these machines is less than 61g is now 0.157.
(d) Find the value of σ .
Answer/Explanation
Ans:
(a) P(C< 61)
= 0.365112…
= 0.365
(b) recognition of binomial eg X ˜ B(12,0.365…)
P( x = 5) = 0.213666…
= 0.214
(c) (i) Let CM represent ‘chocolate muffin’ and BM represent ‘banana muffin’
P(B<61) = 0.0197555…
EITHER
P(CM) × P(C<61|CM) + P(BM) × P(B<61|BM) (or equivalent in words)
OR
tree diagram showing two ways to have a muffin weigh < 61
THEN
(0.6 × 0.365…) + (0.4 × 0.0197…)
= 0.226969…
= 0.227
(ii) recognizing conditional probability
Note: Recognition must be shown in context either in words or symbols, not just P (A|B) .
\(\frac{0.6\times 0.365112…}{0.22699…}\)
= 0.965183…
= 0.965
(d) METHOD 1
P(CM) × P(C<61|CM) + P(BM) × P(B<61|BM) = 0.157
(0.6 × P(C<61))+ (0.4 × 0.0197555….) = 0.157
P(C<61) = 0.248496….
attempt to solve for σ using GDC
Note: Award (M1) for a graph or table of values to show their P (C<61) with a variable standard deviation.
σ =1.47225…
σ = 1.47 (g)
METHOD 2
P(CM) × P(C<61|CM) + P(BM) × P(B<61|BM) = 0.157
(0.6 × P(C<61))+ (0.4 × 0.0197555….) = 0.157
P(C<61) = 0.248496….
use of inverse normal to find z score of their P(C< 61)
z = −0.679229…
correct substitution
\(\frac{61-62}{\sigma }\) = -0.679229…
σ =1.47225…
σ = 1.47 (g)
Questions 9[Maximum mark 15]
Answers in this question should be given to four significant figures. In a local weekly lottery, tickets cost \($\) 2 each. In the first week of the lottery, a player will receive \($\) D for each ticket, with the probability distribution shown in the following table. For example, the probability of a player receiving \($\) 10 is 0.03. The grand prize in the first week of the lottery is \($\) 1000.

(a) Find the value of c.
(b) Determine whether this lottery is a fair game in the first week. Justify your answer.
If nobody wins the grand prize in the first week, the probabilities will remain the same, but the
value of the grand prize will be\($\) 2000 in the second week, and the value of the grand prize
will continue to double each week until it is won. All other prize amounts will remain the same.
(c) Given that the grand prize is not won and the grand prize continues to double, write an
expression in terms of n for the value of the grand prize in the nth week of the lottery.
The wth week is the first week in which the player is expected to make a profit.
Ryan knows that if he buys a lottery ticket in the wth week, his expected profit is \($\)p.
(d) Find the value of p.
Answer/Explanation
(a) considering that sum of probabilities is 1
0.85+c+0.03+0.0002+0.0001=1
0.1179
(b) valid attempt to find \(E\left ( D \right )=\left ( 0\times 0.85 \right )+\left ( 2\times 0.1179 \right )+\left ( 10\times 0.03 \right )+\left ( 50\times 0.0002 \right )+\left ( 1000\times 0.0001 \right )\)
\(E\left ( D \right )=\left ( 0\times 0.7358 \right )\)
No, not a fair game for a fair game,E(D) would be $2 Or players expectes winnings are 1.264
(c) recognition of GP with R=2
\(1000\times 2^{n-1}\) Or \( 500\left ( 2^{n} \right )\)
(d)

Question: [Maximum mark: 6]
A discrete random variable, X, has the following probability distribution:
| x | 0 | 1 | 2 | 3 |
| P(X=x) | 0.41 | k – 0.28 | 0.46 | 0.29-2k2 |
(a) Show that 2k2 – k + 0.12 = 0.
(b) Find the value of k , giving a reason for your answer.
(c) Hence, find E(X).
Answer/Explanation
Ans:
(a) 0.41 + k – 0.28 + 0.46 + 0.29 – 2k2 = 1 OR k – 2k2 + 0.01 = 0.13 (or equivalent)
2k2 – k + 0.12 = 0
(b) one of 0.2 OR 0.3
k = 0.3
reasoning to reject k = 0.2 eg P(1) = k-0.28 ≥ 0 therefore k ≠ 0.2
(c) attempting to use the expected value formula
E(X) = 0 × 0.41 + 1 × (0.3-0.28)+2 × 0.46+3 × (0.29-2 × 0.32)
= 1.27
Note: Award M1A0 if additional values are given.
Question
A discrete random variable X has the following probability distribution.
x | 0 | 1 | 2 | 3 |
P(X = x) | q | 4 p2 | p | 0.7 – 4 p2 |
Find an expression for q in terms of p . [2]
(i) Find the value of p which gives the largest value of E(X).
(ii) Hence, find the largest value of E(X). [4]
Answer/Explanation
Ans

Question
The following table shows the probability distribution of a discrete random variable X.

Find the value of k.
Find the expected value of X.
Answer/Explanation
Markscheme
evidence of using \(\sum {{p_i} = 1} \) (M1)
correct substitution A1
e.g. \(10{k^2} + 3k + 0.6 = 1\) , \(10{k^2} + 3k – 0.4 = 0\)
\(k = 0.1\) A2 N2
[4 marks]
evidence of using \({\rm{E}}(X) = \sum {{p_i}{x_i}} \) (M1)
correct substitution (A1)
e.g. \( – 1 \times 0.2 + 2 \times 0.4 + 3 \times 0.3\)
\({\rm{E}}(X) = 1.5\) A1 N2
[3 marks]
Question
A test has five questions. To pass the test, at least three of the questions must be answered correctly.
The probability that Mark answers a question correctly is \(\frac{1}{5}\) . Let X be the number of questions that Mark answers correctly.
Bill also takes the test. Let Y be the number of questions that Bill answers correctly.
The following table is the probability distribution for Y .
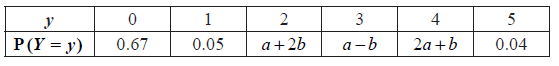
(i) Find E(X ) .
(ii) Find the probability that Mark passes the test.
(i) Show that \(4a + 2b = 0.24\) .
(ii) Given that \({\rm{E}}(Y) = 1\) , find a and b .
Find which student is more likely to pass the test.
Answer/Explanation
Markscheme
(i) valid approach (M1)
e.g. \(np\) , \(5 \times \frac{1}{5}\)
\({\rm{E}}(X) = 1\) A1 N2
(ii) evidence of appropriate approach involving binomial (M1)
e.g. \(X \sim B\left( {5,\frac{1}{5}} \right)\)
recognizing that Mark needs to answer 3 or more questions correctly (A1)
e.g. \({\rm{P}}(X \ge 3)\)
valid approach M1
e.g. \(1 – {\rm{P}}(X \le 2)\) , \({\rm{P}}(X = 3) + {\rm{P}}(X = 4) + {\rm{P}}(X = 5)\)
\({\text{P(pass)}} = 0.0579\) A1 N3
[6 marks]
(i) evidence of summing probabilities to 1 (M1)
e.g. \(0.67 + 0.05 + (a + 2b) + \ldots + 0.04 = 1\)
some simplification that clearly leads to required answer
e.g. \(0.76 + 4a + 2b = 1\) A1
\(4a + 2b = 0.24\) AG N0
(ii) correct substitution into the formula for expected value (A1)
e.g. \(0(0.67) + 1(0.05) + \ldots + 5(0.04)\)
some simplification (A1)
e.g. \(0.05 + 2a + 4b + \ldots + 5(0.04) = 1\)
correct equation A1
e.g. \(13a + 5b = 0.75\)
evidence of solving (M1)
\(a = 0.05\) , \(b = 0.02\) A1A1 N4
[8 marks]
attempt to find probability Bill passes (M1)
e.g. \({\rm{P}}(Y \ge 3)\)
correct value 0.19 A1
Bill (is more likely to pass) A1 N0
[3 marks]
Question
[without GDC]
The probability distribution of the discrete random variable X is given by the table.

Nikos selects a number at random.
If he selects \(1\) he earns \(10\) €. If he selects \(2\) he earns \(5\) €. If he selects \(3\) he loses \(4\) €
(a) Find the expected value of \(X\).
(b) Find the expected value of the profit for Nikos. Is the game fair?
Answer/Explanation
Ans
\(E(X)\) = \(2.2\)\) E(Profit) = \(0\), so it is fair.
