Question
Find the value of \(\int_{1}^{9}\left ( \frac{3\sqrt{x}-5}{\sqrt{x}} \right )dx.\)
▶️Answer/Explanation
Ans:
\(\int \frac{3\sqrt{x}-5}{\sqrt{x}}dx = \int \left ( 3-5x^{-\frac{1}{2}} \right )dx\)
\(\int \frac{3\sqrt{x}-5}{\sqrt{x}}dx = 3x-10x^{\frac{1}{2}}(+c)\)
substituting limits into their integrated function and subtracting
\(3(9) – 10(9)^{\frac{1}{2}} – \left ( 3(1) – 10(1)^{\frac{1}{2}} \right ) OR 27-10\times 3-(3-10)\)
= 4
Question
By using the substitution u = sec x or otherwise, find an expression for \(\int_{0}^{\frac{\pi }{3}} sec^{n} x tan x dx\) in terms of n, where n is a non-zero real number.
▶️Answer/Explanation
Ans:
METHOD 1
U = sec x Þ du = sec x tan x dx
attempts to express the integral in terms of u
\(\int_{1}^{\frac{2} u^{n-1} du\)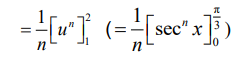
Note: Condone the absence of or incorrect limits up to this point.
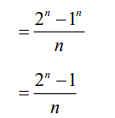
Note: Award M1 for correct substitution of their limits for u into their antiderivative for u ( or given limits for x into their antiderivative for x).
METHOD 2
\(\int sec^{n} x tan x dx = \int sec^{n-1} x sec x tan x dx\)
applies integration by inspection
\(=\frac{1}{n}\left [ sec^{n}x \right ]^{\frac{\pi }{3}}\)
Note: Award A2 if the limits are not stated.
\(=\frac{1}{n} \left ( sec^{n}\frac{\pi }{3}-sec^{n}0 \right )\)
Note: Award M1 for correct substitution into their antiderivative.
=\(\frac{2^{n}-1}{n}\)
Question
By using the substitution u = sec x or otherwise, find an expression for \(\int_{0}^{\frac{\pi }{3}} sec^{n} x tan x dx\) in terms of n, where n is a non-zero real number.
▶️Answer/Explanation
Ans:
METHOD 1
U = sec x Þ du = sec x tan x dx
attempts to express the integral in terms of u
\(\int_{1}^{\frac{2} u^{n-1} du\)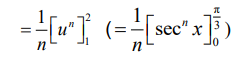
Note: Condone the absence of or incorrect limits up to this point.
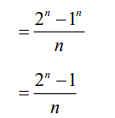
Note: Award M1 for correct substitution of their limits for u into their antiderivative for u ( or given limits for x into their antiderivative for x).
METHOD 2
\(\int sec^{n} x tan x dx = \int sec^{n-1} x sec x tan x dx\)
applies integration by inspection
\(=\frac{1}{n}\left [ sec^{n}x \right ]^{\frac{\pi }{3}}\)
Note: Award A2 if the limits are not stated.
\(=\frac{1}{n} \left ( sec^{n}\frac{\pi }{3}-sec^{n}0 \right )\)
Note: Award M1 for correct substitution into their antiderivative.
=\(\frac{2^{n}-1}{n}\)
