Question
Consider the function f defined by f (x) = 90e-0.5x for x ∈ R+ The graph of f and the line y = x intersect at point P.
Find the x-coordinate of P. [2]
The line L has a gradient of –1 and is a tangent to the graph of f at the point Q.
Find the exact coordinates of Q. [4]
Show that the equation of L is y = -x + 2ln45 + 2 . [2]
The shaded region A is enclosed by the graph of f and the lines y = x and L .
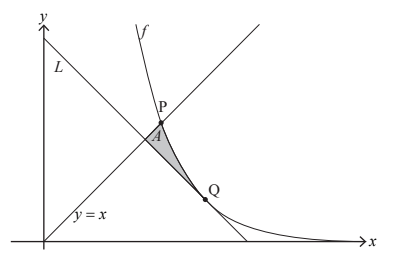
(i) Find the x-coordinate of the point where L intersects the line y = x .
(ii) Hence, find the area of A . [5]
The line L is tangent to the graphs of both f and the inverse function f –1 .
Find the shaded area enclosed by the graphs of f and f –1 and the line L . [2]
Answer/Explanation
Ans:
(a)
attempt to find the point of intersection of the graph of f and the line y = x
x = 5.56619… = 5.57
(b)
\(f'(x)=-45e^{-0.5x}\)
attempt to set the gradient of equal to -1
-45e -0.5x = -1
Q has coordinates \((2ln45,2) \)or \((-2 ln\frac{1}{45},2)\)
(c)
attempt to substitute coordinates of Q ( in any order) into an appropriate equation
y-2= -(x-2ln45)
OR
2= – 2 ln 45 + C
equation of L is y = – x+ 2ln 45 + 2
(d)
(i) x= ln45 + 1 (=4.81)
(ii) appropriate method to find the sum of two areas using integrals of the difference of two functions 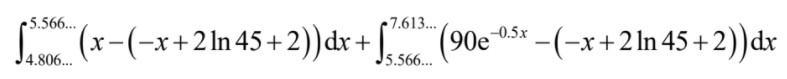
=1.51965… =1.52
(e) by symmetry 2 ×1.52
= 3.03930… = 3.04
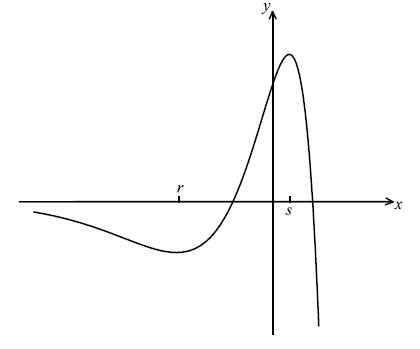
Question
Let \(f(x) = {{\rm{e}}^x}(1 – {x^2})\) .
Part of the graph of \(y = f(x)\), for \( – 6 \le x \le 2\) , is shown below. The x-coordinates of the local minimum and maximum points are r and s respectively.
Show that \(f'(x) = {{\rm{e}}^x}(1 – 2x – {x^2})\) .
Write down the equation of the horizontal asymptote.
Write down the value of r and of s.
Let L be the normal to the curve of f at \({\text{P}}(0{\text{, }}1)\) . Show that L has equation \(x + y = 1\) .
Let R be the region enclosed by the curve \(y = f(x)\) and the line L.
(i) Find an expression for the area of R.
(ii) Calculate the area of R.
Answer/Explanation
Markscheme
evidence of using the product rule M1
\(f'(x) = {{\rm{e}}^x}(1 – {x^2}) + {{\rm{e}}^x}( – 2x)\) A1A1
Note: Award A1 for \({{\rm{e}}^x}(1 – {x^2})\) , A1 for \({{\rm{e}}^x}( – 2x)\) .
\(f'(x) = {{\rm{e}}^x}(1 – 2x – {x^2})\) AG N0
[3 marks]
\(y = 0\) A1 N1
[1 mark]
at the local maximum or minimum point
\(f'(x) = 0\) \(({{\rm{e}}^x}(1 – 2x – {x^2}) = 0)\) (M1)
\( \Rightarrow 1 – 2x – {x^2} = 0\) (M1)
\(r = – 2.41\) \(s = 0.414\) A1A1 N2N2
[4 marks]
\(f'(0) = 1\) A1
gradient of the normal \(= – 1\) A1
evidence of substituting into an equation for a straight line (M1)
correct substitution A1
e.g. \(y – 1 = – 1(x – 0)\) , \(y – 1 = – x\) , \(y = – x + 1\)
\(x + y = 1\) AG N0
[4 marks]
(i) intersection points at \(x = 0\) and \(x = 1\) (may be seen as the limits) (A1)
approach involving subtraction and integrals (M1)
fully correct expression A2 N4
e.g. \(\int_0^1 {\left( {{{\rm{e}}^x}(1 – {x^2}) – (1 – x)} \right)} {\rm{d}}x\) , \(\int_0^1 {f(x){\rm{d}}x – \int_0^1 {(1 – x){\rm{d}}x} } \)
(ii) area \(R = 0.5\) A1 N1
[5 marks]
Question
Let \(f(x) = {{\rm{e}}^{2x}}\cos x\) , \( – 1 \le x \le 2\) .
Show that \(f'(x) = {{\rm{e}}^{2x}}(2\cos x – \sin x)\) .
Let the line L be the normal to the curve of f at \(x = 0\) .
Find the equation of L .
The graph of f and the line L intersect at the point (0, 1) and at a second point P.
(i) Find the x-coordinate of P.
(ii) Find the area of the region enclosed by the graph of f and the line L .
Answer/Explanation
Markscheme
correctly finding the derivative of \({{\rm{e}}^{2x}}\) , i.e. \(2{{\rm{e}}^{2x}}\) A1
correctly finding the derivative of \(\cos x\) , i.e. \( – \sin x\) A1
evidence of using the product rule, seen anywhere M1
e.g. \(f'(x) = 2{{\rm{e}}^{2x}}\cos x – {{\rm{e}}^{2x}}\sin x\)
\(f'(x) = 2{{\rm{e}}^{2x}}(2\cos x – \sin x)\) AG N0
[3 marks]
evidence of finding \(f(0) = 1\) , seen anywhere A1
attempt to find the gradient of f (M1)
e.g. substituting \(x = 0\) into \(f'(x)\)
value of the gradient of f A1
e.g. \(f'(0) = 2\) , equation of tangent is \(y = 2x + 1\)
gradient of normal \( = – \frac{1}{2}\) (A1)
\(y – 1 = – \frac{1}{2}x\left( {y = – \frac{1}{2}x + 1} \right)\) A1 N3
[5 marks]
(i) evidence of equating correct functions M1
e.g. \({{\rm{e}}^{2x}}\cos x = – \frac{1}{2}x + 1\) , sketch showing intersection of graphs
\(x = 1.56\) A1 N1
(ii) evidence of approach involving subtraction of integrals/areas (M1)
e.g. \(\int {\left[ {f(x) – g(x)} \right]} {\rm{d}}x\) , \(\int {f(x)} {\rm{d}}x – {\text{area under trapezium}}\)
fully correct integral expression A2
e.g. \(\int_0^{1.56} {\left[ {{{\rm{e}}^{2x}}\cos x – \left( { – \frac{1}{2}x + 1} \right)} \right]} {\rm{d}}x\) , \(\int_0^{1.56} {{{\rm{e}}^{2x}}\cos x} {\rm{d}}x – 0.951 \ldots \)
\({\rm{area}} = 3.28\) A1 N2
[6 marks]
