Question
Let \(f(x) = 3\sin x + 4\cos x\) , for \( – 2\pi \le x \le 2\pi \) .
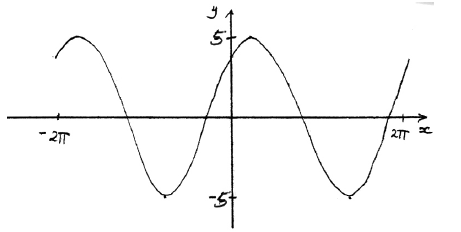
Sketch the graph of f .
Write down
(i) the amplitude;
(ii) the period;
(iii) the x-intercept that lies between \( – \frac{\pi }{2}\) and 0.
Hence write \(f(x)\) in the form \(p\sin (qx + r)\) .
Write down one value of x such that \(f'(x) = 0\) .
Write down the two values of k for which the equation \(f(x) = k\) has exactly two solutions.
Let \(g(x) = \ln (x + 1)\) , for \(0 \le x \le \pi \) . There is a value of x, between \(0\) and \(1\), for which the gradient of f is equal to the gradient of g. Find this value of x.
Answer/Explanation
Markscheme
A1A1A1 N3
Note: Award A1 for approximately sinusoidal shape, A1 for end points approximately correct \(( – 2\pi {\text{, }}4)\) \((2\pi {\text{, }}4)\), A1 for approximately correct position of graph, (y-intercept \((0{\text{, }}4)\), maximum to right of y-axis).
[3 marks]
(i) 5 A1 N1
(ii) \(2\pi \) (6.28) A1 N1
(iii) \( – 0.927\) A1 N1
[3 marks]
\(f(x) = 5\sin (x + 0.927)\) (accept \(p = 5\) , \(q = 1\) , \(r = 0.927\) ) A1A1A1 N3
[3 marks]
evidence of correct approach (M1)
e.g. max/min, sketch of \(f'(x)\) indicating roots
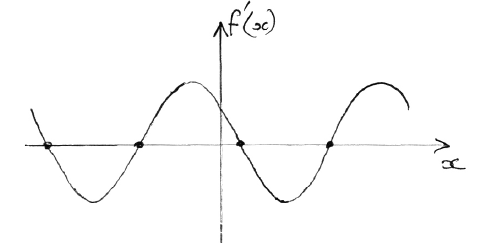
one 3 s.f. value which rounds to one of \( – 5.6\), \( – 2.5\), \(0.64\), \(3.8\) A1 N2
[2 marks]
\(k = – 5\) , \(k = 5\) A1A1 N2
[2 marks]
METHOD 1
graphical approach (but must involve derivative functions) M1
e.g.
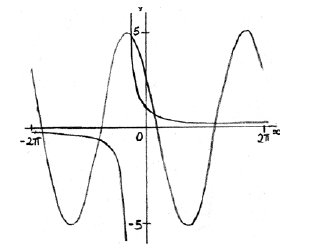
each curve A1A1
\(x = 0.511\) A2 N2
METHOD 2
\(g'(x) = \frac{1}{{x + 1}}\) A1
\(f'(x) = 3\cos x – 4\sin x\) \((5\cos (x + 0.927))\) A1
evidence of attempt to solve \(g'(x) = f'(x)\) M1
\(x = 0.511\) A2 N2
[5 marks]
Question
Consider \(f(x) = x\ln (4 – {x^2})\) , for \( – 2 < x < 2\) . The graph of f is given below.
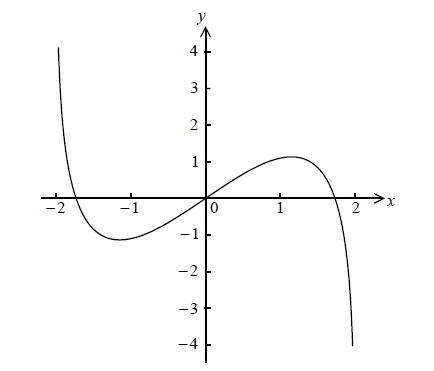
Let P and Q be points on the curve of f where the tangent to the graph of f is parallel to the x-axis.
(i) Find the x-coordinate of P and of Q.
(ii) Consider \(f(x) = k\) . Write down all values of k for which there are exactly two solutions.
Let \(g(x) = {x^3}\ln (4 – {x^2})\) , for \( – 2 < x < 2\) .
Show that \(g'(x) = \frac{{ – 2{x^4}}}{{4 – {x^2}}} + 3{x^2}\ln (4 – {x^2})\) .
Let \(g(x) = {x^3}\ln (4 – {x^2})\) , for \( – 2 < x < 2\) .
Sketch the graph of \(g’\) .
Let \(g(x) = {x^3}\ln (4 – {x^2})\) , for \( – 2 < x < 2\) .
Consider \(g'(x) = w\) . Write down all values of w for which there are exactly two solutions.
Answer/Explanation
Markscheme
(i) \( – 1.15{\text{, }}1.15\) A1A1 N2
(ii) recognizing that it occurs at P and Q (M1)
e.g. \(x = – 1.15\) , \(x = 1.15\)
\(k = – 1.13\) , \(k = 1.13\) A1A1 N3
[5 marks]
evidence of choosing the product rule (M1)
e.g. \(uv’ + vu’\)
derivative of \({x^3}\) is \(3{x^2}\) (A1)
derivative of \(\ln (4 – {x^2})\) is \(\frac{{ – 2x}}{{4 – {x^2}}}\) (A1)
correct substitution A1
e.g. \({x^3} \times \frac{{ – 2x}}{{4 – {x^2}}} + \ln (4 – {x^2}) \times 3{x^2}\)
\(g'(x) = \frac{{ – 2{x^4}}}{{4 – {x^2}}} + 3{x^2}\ln (4 – {x^2})\) AG N0
[4 marks]
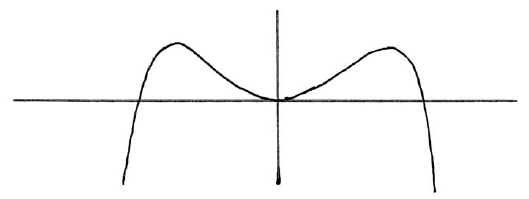A1A1 N2
[2 marks]
\(w = 2.69\) , \(w < 0\) A1A2 N2
[3 marks]
Question
Let \(f(x) = x\cos x\) , for \(0 \le x \le 6\) .
Find \(f'(x)\) .
On the grid below, sketch the graph of \(y = f'(x)\) .
Answer/Explanation
Markscheme
evidence of choosing the product rule (M1)
e.g. \(x \times ( – \sin x) + 1 \times \cos x\)
\(f'(x) = \cos x – x\sin x\) A1A1 N3
[3 marks]
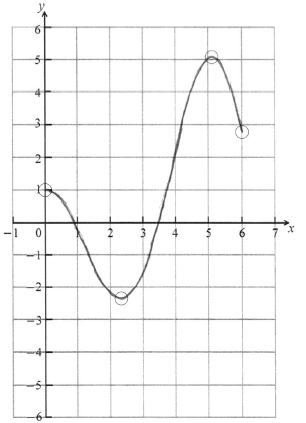A1A1A1A1 N4
Note: Award A1 for correct domain, \(0 \le x \le 6\) with endpoints in circles, A1 for approximately correct shape, A1 for local minimum in circle, A1 for local maximum in circle.
[4 marks]
Question
Let \(f(x) = \cos 2x\) and \(g(x) = \ln (3x – 5)\) .
Find \(f'(x)\) .
Find \(g'(x)\) .
Let \(h(x) = f(x) \times g(x)\) . Find \(h'(x)\) .
Answer/Explanation
Markscheme
(a) \(f'(x) = – \sin 2x \times 2( = – 2\sin 2x)\) A1A1 N2
Note: Award A1 for 2, A1 for \( – \sin 2x\) .
[2 marks]
\(g'(x) = 3 \times \frac{1}{{3x – 5}}\) \(\left( { = \frac{3}{{3x – 5}}} \right)\) A1A1 N2
Note: Award A1 for 3, A1 for \(\frac{1}{{3x – 5}}\) .
[2 marks]
evidence of using product rule (M1)
\(h'(x) = (\cos 2x)\left( {\frac{3}{{3x – 5}}} \right) + \ln (3x – 5)( – 2\sin 2x)\) A1 N2
[2 marks]
Question
Let \(f(x) = \sqrt[3]{{{x^4}}} – \frac{1}{2}\).
Find \(f'(x)\).
Find \(\int {f(x){\text{d}}x} \).
Answer/Explanation
Markscheme
expressing \(f\) as \({x^{\frac{4}{3}}}\) (M1)
\(f'(x) = \frac{4}{3}{x^{\frac{1}{3}}}{\text{ }}\left( { = \frac{4}{3}\sqrt[3]{x}} \right)\) A1 N2
[2 marks]
attempt to integrate \({\sqrt[3]{{{x^4}}}}\) (M1)
eg \(\frac{{{x^{\frac{4}{3} + 1}}}}{{\frac{4}{3} + 1}}\)
\(\int {f(x){\text{d}}x = \frac{3}{7}{x^{\frac{7}{3}}} – \frac{x}{2} + c} \) A1A1A1 N4
[4 marks]
Question
Let \(f(x) = \frac{1}{{x – 1}} + 2\), for \(x > 1\).
Let \(g(x) = a{e^{ – x}} + b\), for \(x \geqslant 1\). The graphs of \(f\) and \(g\) have the same horizontal asymptote.
Write down the equation of the horizontal asymptote of the graph of \(f\).
Find \(f'(x)\).
Write down the value of \(b\).
Given that \(g'(1) = – e\), find the value of \(a\).
There is a value of \(x\), for \(1 < x < 4\), for which the graphs of \(f\) and \(g\) have the same gradient. Find this gradient.
Answer/Explanation
Markscheme
\(y = 2\) (correct equation only) A2 N2
[2 marks]
valid approach (M1)
eg\(\,\,\,\,\,\)\({(x – 1)^{ – 1}} + 2,{\text{ }}f'(x) = \frac{{0(x – 1) – 1}}{{{{(x – 1)}^2}}}\)
\( – {(x – 1)^{ – 2}},{\text{ }}f'(x) = \frac{{ – 1}}{{{{(x – 1)}^2}}}\) A1 N2
[2 marks]
correct equation for the asymptote of \(g\)
eg\(\,\,\,\,\,\)\(y = b\) (A1)
\(b = 2\) A1 N2
[2 marks]
correct derivative of g (seen anywhere) (A2)
eg\(\,\,\,\,\,\)\(g'(x) = – a{{\text{e}}^{ – x}}\)
correct equation (A1)
eg\(\,\,\,\,\,\)\( – {\text{e}} = – a{{\text{e}}^{ – 1}}\)
7.38905
\(a = {{\text{e}}^2}{\text{ }}({\text{exact}}),{\text{ }}7.39\) A1 N2
[4 marks]
attempt to equate their derivatives (M1)
eg\(\,\,\,\,\,\)\(f'(x) = g'(x),{\text{ }}\frac{{ – 1}}{{{{(x – 1)}^2}}} = – a{{\text{e}}^{ – x}}\)
valid attempt to solve their equation (M1)
eg\(\,\,\,\,\,\)correct value outside the domain of \(f\) such as 0.522 or 4.51,
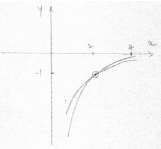
correct solution (may be seen in sketch) (A1)
eg\(\,\,\,\,\,\)\(x = 2,{\text{ }}(2,{\text{ }} – 1)\)
gradient is \( – 1\) A1 N3
[4 marks]
Question
Let \(f(x) = {({x^2} + 3)^7}\). Find the term in \({x^5}\) in the expansion of the derivative, \(f’(x)\).
Answer/Explanation
Markscheme
METHOD 1
derivative of \(f(x)\) A2
\(7{({x^2} + 3)^6}(x2)\)
recognizing need to find \({x^4}\) term in \({({x^2} + 3)^6}\) (seen anywhere) R1
eg\(\,\,\,\,\,\)\(14x{\text{ (term in }}{x^4})\)
valid approach to find the terms in \({({x^2} + 3)^6}\) (M1)
eg\(\,\,\,\,\,\)\(\left( {\begin{array}{*{20}{c}} 6 \\ r \end{array}} \right){({x^2})^{6 – r}}{(3)^r},{\text{ }}{({x^2})^6}{(3)^0} + {({x^2})^5}{(3)^1} + \ldots \), Pascal’s triangle to 6th row
identifying correct term (may be indicated in expansion) (A1)
eg\(\,\,\,\,\,\)\({\text{5th term, }}r = 2,{\text{ }}\left( {\begin{array}{*{20}{c}} 6 \\ 4 \end{array}} \right),{\text{ }}{({x^2})^2}{(3)^4}\)
correct working (may be seen in expansion) (A1)
eg\(\,\,\,\,\,\)\(\left( {\begin{array}{*{20}{c}} 6 \\ 4 \end{array}} \right){({x^2})^2}{(3)^4},{\text{ }}15 \times {3^4},{\text{ }}14x \times 15 \times 81{({x^2})^2}\)
\(17010{x^5}\) A1 N3
METHOD 2
recognition of need to find \({x^6}\) in \({({x^2} + 3)^7}\) (seen anywhere) R1
valid approach to find the terms in \({({x^2} + 3)^7}\) (M1)
eg\(\,\,\,\,\,\)\(\left( {\begin{array}{*{20}{c}} 7 \\ r \end{array}} \right){({x^2})^{7 – r}}{(3)^r},{\text{ }}{({x^2})^7}{(3)^0} + {({x^2})^6}{(3)^1} + \ldots \), Pascal’s triangle to 7th row
identifying correct term (may be indicated in expansion) (A1)
eg\(\,\,\,\,\,\)6th term, \(r = 3,{\text{ }}\left( {\begin{array}{*{20}{c}} 7 \\ 3 \end{array}} \right),{\text{ (}}{{\text{x}}^2}{)^3}{(3)^4}\)
correct working (may be seen in expansion) (A1)
eg\(\,\,\,\,\,\)\(\left( {\begin{array}{*{20}{c}} 7 \\ 4 \end{array}} \right){{\text{(}}{{\text{x}}^2})^3}{(3)^4},{\text{ }}35 \times {3^4}\)
correct term (A1)
\(2835{x^6}\)
differentiating their term in \({x^6}\) (M1)
eg\(\,\,\,\,\,\)\((2835{x^6})’,{\text{ (6)(2835}}{{\text{x}}^5})\)
\(17010{x^5}\) A1 N3
[7 marks]
Question
[without GDC]
Let \(f(x)=\frac{3x^{2}}{5x-1}\)
(a) Write down the equation of the vertical asymptote of \(y=f(x)\).
(b) Find \(f'(x)\). Give your answer in the form \(\frac{ax^{2}+bx}{(5x-1)^{2}}\) where \(a\) and \(b \, \epsilon\, \mathbb{Z}\).
Answer/Explanation
Ans
(a) \(x=\frac{1}{5}\)
(b) \(f'(x)=\frac{(5x-1)(6x)-(3x^{2})(5)}{(5x-1)^{2}}=\frac{30x^{2}-6x-15x^{2}}{(5x-1)^{2}}=\frac{15x^{2}-6x}{(5x-1)^{2}}\)