Question
Consider a function f (x), for x ≥ 0. The derivative of f is given by f ′(x) = \(\frac{6x}{x^2+4}\)
Show that f ′′(x) = \(\frac{24-6x^2}{(x^2+4)^2}\) . [4]
The graph of f is concave-down when x > n .
Find the least value of n . [2]
Find \(\int \frac{6x}{x2+4}dx\) . [3]
Let R be the region enclosed by the graph of f , the x-axis and the lines x = 1 and x = 3 .
The area of R is 19.6, correct to three significant figures.
Find f (x). [7]
Answer/Explanation
Ans



Question
The following diagram shows the graph of \(f(x) = {{\rm{e}}^{ – {x^2}}}\) .
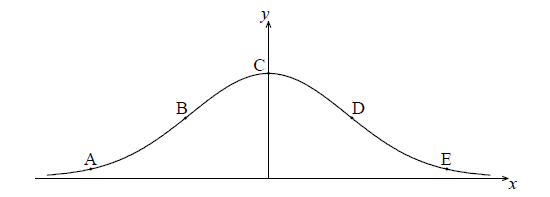
The points A, B, C, D and E lie on the graph of f . Two of these are points of inflexion.
Identify the two points of inflexion.
(i) Find \(f'(x)\) .
(ii) Show that \(f”(x) = (4{x^2} – 2){{\rm{e}}^{ – {x^2}}}\) .
Find the x-coordinate of each point of inflexion.
Use the second derivative to show that one of these points is a point of inflexion.
Answer/Explanation
Markscheme
B, D A1A1 N2
[2 marks]
(i) \(f'(x) = – 2x{{\rm{e}}^{ – {x^2}}}\) A1A1 N2
Note: Award A1 for \({{\rm{e}}^{ – {x^2}}}\) and A1 for \( – 2x\) .
(ii) finding the derivative of \( – 2x\) , i.e. \( – 2\) (A1)
evidence of choosing the product rule (M1)
e.g. \( – 2{{\rm{e}}^{ – {x^2}}}\) \( – 2x \times – 2x{{\rm{e}}^{ – {x^2}}}\)
\( – 2{{\rm{e}}^{ – {x^2}}} + 4{x^2}{{\rm{e}}^{ – {x^2}}}\) A1
\(f”(x) = (4{x^2} – 2){{\rm{e}}^{ – {x^2}}}\) AG N0
[5 marks]
valid reasoning R1
e.g. \(f”(x) = 0\)
attempting to solve the equation (M1)
e.g. \((4{x^2} – 2) = 0\) , sketch of \(f”(x)\)
\(p = 0.707\) \(\left( { = \frac{1}{{\sqrt 2 }}} \right)\) , \(q = – 0.707\) \(\left( { = – \frac{1}{{\sqrt 2 }}} \right)\) A1A1 N3
[4 marks]
evidence of using second derivative to test values on either side of POI M1
e.g. finding values, reference to graph of \(f”\) , sign table
correct working A1A1
e.g. finding any two correct values either side of POI,
checking sign of \(f”\) on either side of POI
reference to sign change of \(f”(x)\) R1 N0
[4 marks]
Question
The diagram below shows part of the graph of the gradient function, \(y = f'(x)\) .
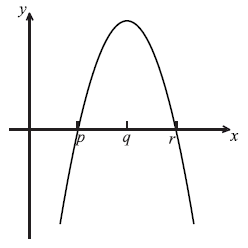
On the grid below, sketch a graph of \(y = f”(x)\) , clearly indicating the x-intercept.
Complete the table, for the graph of \(y = f(x)\) .

Justify your answer to part (b) (ii).
Answer/Explanation
Markscheme
A1A1 N2
Note: Award A1 for negative gradient throughout, A1 for x-intercept of q. It need not be linear.
[2 marks]
 A1A1 N1N1
A1A1 N1N1
METHOD 1
Second derivative is zero, second derivative changes sign. R1R1 N2
METHOD 2
There is a maximum on the graph of the first derivative. R2 N2
Question
Consider a function \(f\), for \(0 \le x \le 10\). The following diagram shows the graph of \(f’\), the derivative of \(f\).
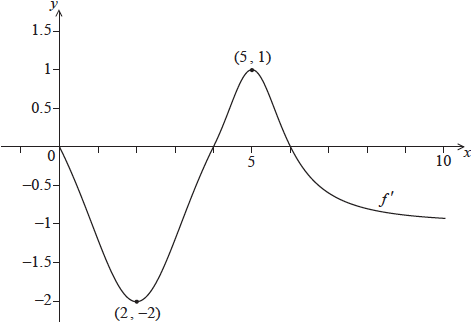
The graph of \(f’\) passes through \((2,{\text{ }} – 2)\) and \((5,{\text{ }}1)\), and has \(x\)-intercepts at \(0\), \(4\) and \(6\).
The graph of \(f\) has a local maximum point when \(x = p\). State the value of \(p\), and justify your answer.
Write down \(f'(2)\).
Let \(g(x) = \ln \left( {f(x)} \right)\) and \(f(2) = 3\).
Find \(g'(2)\).
Verify that \(\ln 3 + \int_2^a {g'(x){\text{d}}x = g(a)} \), where \(0 \le a \le 10\).
The following diagram shows the graph of \(g’\), the derivative of \(g\).
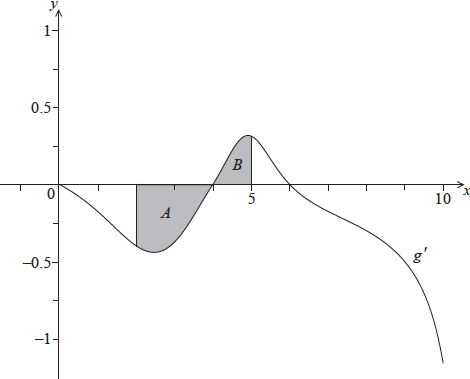
The shaded region \(A\) is enclosed by the curve, the \(x\)-axis and the line \(x = 2\), and has area \({\text{0.66 unit}}{{\text{s}}^{\text{2}}}\).
The shaded region \(B\) is enclosed by the curve, the \(x\)-axis and the line \(x = 5\), and has area \({\text{0.21 unit}}{{\text{s}}^{\text{2}}}\).
Find \(g(5)\).
Answer/Explanation
Markscheme
\(p = 6\) A1 N1
recognizing that turning points occur when \(f'(x) = 0\) R1 N1
eg\(\;\;\;\)correct sign diagram
\(f’\) changes from positive to negative at \(x = 6\) R1 N1
[3 marks]
\(f'(2) = – 2\) A1 N1
[1 mark]
attempt to apply chain rule (M1)
eg\(\;\;\;\ln (x)’ \times f'(x)\)
correct expression for \(g'(x)\) (A1)
eg\(\;\;\;g'(x) = \frac{1}{{f(x)}} \times f'(x)\)
substituting \(x = 2\) into their \(g’\) (M1)
eg\(\;\;\;\frac{{f'(2)}}{{f(2)}}\)
\( – 0.666667\)
\(g'(2) = – \frac{2}{3}{\text{ (exact), }} – 0.667\) A1 N3
[4 marks]
evidence of integrating \(g'(x)\) (M1)
eg\(\;\;\;g(x)|_2^a,{\text{ }}g(x)|_a^2\)
applying the fundamental theorem of calculus (seen anywhere) R1
eg\(\;\;\;\int_2^a {g'(x) = g(a) – g(2)} \)
correct substitution into integral (A1)
eg\(\;\;\;\ln 3 + g(a) – g(2),{\text{ }}\ln 3 + g(a) – \ln \left( {f(2)} \right)\)
\(\ln 3 + g(a) – \ln 3\) A1
\(\ln 3 + \int_2^a {g'(x) = g(a)} \) AG N0
[4 marks]
METHOD 1
substituting \(a = 5\) into the formula for \(g(a)\) (M1)
eg\(\;\;\;\int_2^5 {g'(x){\text{d}}x,{\text{ }}g(5) = \ln 3 + \int_2^5 {g'(x){\text{d}}x\;\;\;} } \left( {{\text{do not accept only }}g(5)} \right)\)
attempt to substitute areas (M1)
eg\(\;\;\;\ln 3 + 0.66 – 0.21,{\text{ }}\ln 3 + 0.66 + 0.21\)
correct working
eg\(\;\;\;g(5) = \ln 3 + ( – 0.66 + 0.21)\) (A1)
\(0.648612\)
\(g(5) = \ln 3 – 0.45{\text{ (exact), }}0.649\) A1 N3
METHOD 2
attempt to set up an equation for one shaded region (M1)
eg\(\;\;\;\int_4^5 {g'(x){\text{d}}x = 0.21,{\text{ }}\int_2^4 {g'(x){\text{d}}x = – 0.66,{\text{ }}\int_2^5 {g'(x){\text{d}}x = – 0.45} } } \)
two correct equations (A1)
eg\(\;\;\;g(5) – g(4) = 0.21,{\text{ }}g(2) – g(4) = 0.66\)
combining equations to eliminate \(g(4)\) (M1)
eg\(\;\;\;g(5) – [\ln 3 – 0.66] = 0.21\)
\(0.648612\)
\(g(5) = \ln 3 – 0.45{\text{ (exact), }}0.649\) A1 N3
METHOD 3
attempt to set up a definite integral (M1)
eg\(\;\;\;\int_2^5 {g'(x){\text{d}}x = – 0.66 + 0.21,{\text{ }}\int_2^5 {g'(x){\text{d}}x = – 0.45} } \)
correct working (A1)
eg\(\;\;\;g(5) – g(2) = – 0.45\)
correct substitution (A1)
eg\(\;\;\;g(5) – \ln 3 = – 0.45\)
\(0.648612\)
\(g(5) = \ln 3 – 0.45{\text{ (exact), }}0.649\) A1 N3
[4 marks]
Total [16 marks]
