Question
The function f is defined by
\[f(x) = {({x^3} + 6{x^2} + 3x – 10)^{\frac{1}{2}}},{\text{ for }}x \in D,\]
where \(D \subseteq \mathbb{R}\) is the greatest possible domain of f.
(a) Find the roots of \(f(x) = 0\).
(b) Hence specify the set D.
(c) Find the coordinates of the local maximum on the graph \(y = f(x)\).
(d) Solve the equation \(f(x) = 3\).
(e) Sketch the graph of \(\left| y \right| = f(x),{\text{ for }}x \in D\).
(f) Find the area of the region completely enclosed by the graph of \(\left| y \right| = f(x)\)
▶️Answer/Explanation
Markscheme
(a) solving to obtain one root: 1, – 2 or – 5 A1
obtain other roots A1
[2 marks]
(b) \(D = x \in [ – 5,{\text{ }} – 2] \cup [1,{\text{ }}\infty {\text{)}}\) (or equivalent) M1A1
Note: M1 is for 1 finite and 1 infinite interval.
[2 marks]
(c) coordinates of local maximum \( – 3.73 – 2 – \sqrt 3 ,{\text{ }}3.22\sqrt {6\sqrt 3 } \) A1A1
[2 marks]
(d) use GDC to obtain one root: 1.41, – 3.18 or – 4.23 A1
obtain other roots A1
[2 marks]
(e)
 A1A1A1
A1A1A1
Note: Award A1 for shape, A1 for max and for min clearly in correct places, A1 for all intercepts.
Award A1A0A0 if only the complete top half is shown.
[3 marks]
(f) required area is twice that of \(y = f(x)\) between – 5 and – 2 M1A1
answer 14.9 A1 N3
Note: Award M1A0A0 for \(\int_{ – 5}^{ – 2} {f(x){\text{d}}x = 7.47 \ldots } \) or N1 for 7.47.
[3 marks]
Total [14 marks]
Examiners report
This was a multi-part question that was well answered by many candidates. The main difficulty was sketching the graph and this meant that the last part was not well answered.
Question
A triangle is formed by the three lines \(y = 10 – 2x,{\text{ }}y = mx\) and \(y = -\frac{1}{m}x\), where \(m > \frac{1}{2}\).
Find the value of m for which the area of the triangle is a minimum.
▶️Answer/Explanation
Markscheme
attempt to find intersections M1
intersections are \(\left( {\frac{{10}}{{m + 2}},\frac{{10m}}{{m + 2}}} \right){\text{ and }}\left( {\frac{{10m}}{{2m – 1}}, – \frac{{10}}{{2m – 1}}} \right)\) A1A1
area of triangle \( = \frac{1}{2} \times \frac{{\sqrt {100 + 100{m^2}} }}{{(m + 2)}} \times \frac{{\sqrt {100 + 100{m^2}} }}{{(2m – 1)}}\) M1A1A1
\( = \frac{{50(1 + {m^2})}}{{(m + 2)(2m – 1)}}\)
minimum when \(m = 3\) (M1)A1
[8 marks]
Examiners report
Most candidates had difficulties with this question and did not go beyond the determination of the intersection points of the lines; in a few cases candidates set up the expression of the area, in some cases using unsimplified expressions of the coordinates.
Question
Two non-intersecting circles C1 , containing points M and S , and C2 , containing points N and R, have centres P and Q where PQ \( = 50\) . The line segments [MN] and [SR] are common tangents to the circles. The size of the reflex angle MPS is \( \alpha\), the size of the obtuse angle NQR is \( \beta\) , and the size of the angle MPQ is \( \theta\) . The arc length MS is \({l_1}\) and the arc length NR is \({l_2}\) . This information is represented in the diagram below.
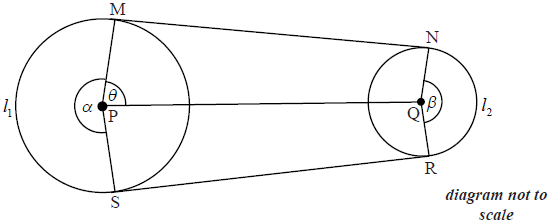
The radius of C1 is \(x\) , where \(x \geqslant 10\) and the radius of C2 is \(10\).
(a) Explain why \(x < 40\) .
(b) Show that cosθ = x −10 50.
(c) (i) Find an expression for MN in terms of \(x\) .
(ii) Find the value of \(x\) that maximises MN.
(d) Find an expression in terms of \(x\) for
(i) \( \alpha\) ;
(ii) \( \beta\) .
(e) The length of the perimeter is given by \({l_1} + {l_2} + {\text{MN}} + {\text{SR}}\).
(i) Find an expression, \(b (x)\) , for the length of the perimeter in terms of \(x\) .
(ii) Find the maximum value of the length of the perimeter.
(iii) Find the value of \(x\) that gives a perimeter of length \(200\).
▶️Answer/Explanation
Markscheme
(a) PQ \( = 50\) and non-intersecting R1
[1 mark]
(b) a construction QT (where T is on the radius MP), parallel to MN, so that \({\text{Q}}\hat {\text{T}}{\text{M}} = 90^\circ \) (angle between tangent and radius \( = 90^\circ \) ) M1
lengths \(50\), \(x – 10\) and angle \( \theta\) marked on a diagram, or equivalent R1
Note: Other construction lines are possible.
[2 marks]
(c) (i) MN \( = \sqrt {{{50}^2} – {{\left( {x – 10} \right)}^2}} \) A1
(ii) maximum for MN occurs when \(x = 10\) A1
[2 marks]
(d) (i) \(\alpha = 2\pi – 2\theta \) M1
\( = 2\pi – 2\arccos \left( {\frac{{x – 10}}{{50}}} \right)\) A1
(ii) \(\beta = 2\pi – \alpha \) ( \( = 2\theta \) ) A1
\( = 2\left( {{{\cos }^{ – 1}}\left( {\frac{{x – 10}}{{50}}} \right)} \right)\) A1
[4 marks]
(e) (i) \(b(x) = x\alpha + 10\beta + 2\sqrt {{{50}^2} – {{\left( {x – 10} \right)}^2}} \) A1A1A1
\( = x\left( {2\pi – 2\left( {{{\cos }^{ – 1}}\left( {\frac{{x – 10}}{{50}}} \right)} \right)} \right) + 20\left( {\left( {{{\cos }^{ – 1}}\left( {\frac{{x – 10}}{{50}}} \right)} \right)} \right) + 2\sqrt {{{50}^2} – {{\left( {x – 10} \right)}^2}} \) M1A1
(ii) maximum value of perimeter \( = 276\) A2
(iii) perimeter of \(200\) cm \(b(x) = 200\) (M1)
when \(x = 21.2\) A1
[9 marks]
Total [18 marks]
Examiners report
This is not an inherently difficult question, but candidates either made heavy weather of it or avoided it almost entirely. The key to answering the question is in obtaining the displayed answer to part (b), for which a construction line parallel to MN through Q is required. Diagrams seen by examiners on some scripts tend to suggest that the perpendicularity property of a tangent to a circle and the associated radius is not as firmly known as they had expected. Some candidates mixed radians and degrees in their expressions.
Question
Two non-intersecting circles C1 , containing points M and S , and C2 , containing points N and R, have centres P and Q where PQ \( = 50\) . The line segments [MN] and [SR] are common tangents to the circles. The size of the reflex angle MPS is \( \alpha\), the size of the obtuse angle NQR is \( \beta\) , and the size of the angle MPQ is \( \theta\) . The arc length MS is \({l_1}\) and the arc length NR is \({l_2}\) . This information is represented in the diagram below.

The radius of C1 is \(x\) , where \(x \geqslant 10\) and the radius of C2 is \(10\).
(a) Explain why \(x < 40\) .
(b) Show that cosθ = x −10 50.
(c) (i) Find an expression for MN in terms of \(x\) .
(ii) Find the value of \(x\) that maximises MN.
(d) Find an expression in terms of \(x\) for
(i) \( \alpha\) ;
(ii) \( \beta\) .
(e) The length of the perimeter is given by \({l_1} + {l_2} + {\text{MN}} + {\text{SR}}\).
(i) Find an expression, \(b (x)\) , for the length of the perimeter in terms of \(x\) .
(ii) Find the maximum value of the length of the perimeter.
(iii) Find the value of \(x\) that gives a perimeter of length \(200\).
▶️Answer/Explanation
Markscheme
(a) PQ \( = 50\) and non-intersecting R1
[1 mark]
(b) a construction QT (where T is on the radius MP), parallel to MN, so that \({\text{Q}}\hat {\text{T}}{\text{M}} = 90^\circ \) (angle between tangent and radius \( = 90^\circ \) ) M1
lengths \(50\), \(x – 10\) and angle \( \theta\) marked on a diagram, or equivalent R1
Note: Other construction lines are possible.
[2 marks]
(c) (i) MN \( = \sqrt {{{50}^2} – {{\left( {x – 10} \right)}^2}} \) A1
(ii) maximum for MN occurs when \(x = 10\) A1
[2 marks]
(d) (i) \(\alpha = 2\pi – 2\theta \) M1
\( = 2\pi – 2\arccos \left( {\frac{{x – 10}}{{50}}} \right)\) A1
(ii) \(\beta = 2\pi – \alpha \) ( \( = 2\theta \) ) A1
\( = 2\left( {{{\cos }^{ – 1}}\left( {\frac{{x – 10}}{{50}}} \right)} \right)\) A1
[4 marks]
(e) (i) \(b(x) = x\alpha + 10\beta + 2\sqrt {{{50}^2} – {{\left( {x – 10} \right)}^2}} \) A1A1A1
\( = x\left( {2\pi – 2\left( {{{\cos }^{ – 1}}\left( {\frac{{x – 10}}{{50}}} \right)} \right)} \right) + 20\left( {\left( {{{\cos }^{ – 1}}\left( {\frac{{x – 10}}{{50}}} \right)} \right)} \right) + 2\sqrt {{{50}^2} – {{\left( {x – 10} \right)}^2}} \) M1A1
(ii) maximum value of perimeter \( = 276\) A2
(iii) perimeter of \(200\) cm \(b(x) = 200\) (M1)
when \(x = 21.2\) A1
[9 marks]
Total [18 marks]
Examiners report
This is not an inherently difficult question, but candidates either made heavy weather of it or avoided it almost entirely. The key to answering the question is in obtaining the displayed answer to part (b), for which a construction line parallel to MN through Q is required. Diagrams seen by examiners on some scripts tend to suggest that the perpendicularity property of a tangent to a circle and the associated radius is not as firmly known as they had expected. Some candidates mixed radians and degrees in their expressions.
Question
Consider the curve with equation \(f(x) = {{\text{e}}^{ – 2{x^2}}}{\text{ for }}x < 0\) .
Find the coordinates of the point of inflexion and justify that it is a point of inflexion.
▶️Answer/Explanation
Markscheme
METHOD 1
EITHER
Using the graph of \(y = f'(x)\) (M1)
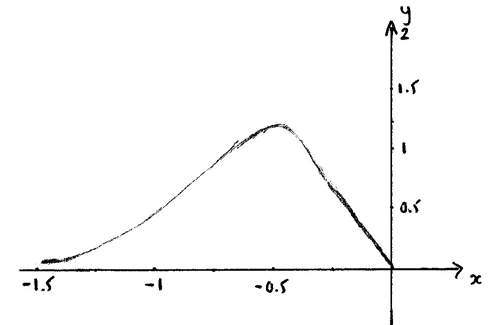 A1
A1
The maximum of \(f'(x)\) occurs at x = −0.5 . A1
OR
Using the graph of \(y = f”(x)\). (M1)
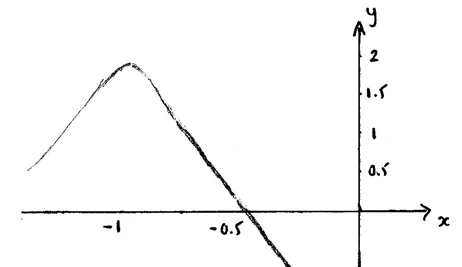 A1
A1
The zero of \(f”(x)\) occurs at x = −0.5 . A1
THEN
Note: Do not award this A1 for stating x = ±0.5 as the final answer for x .
\(f( – 0.5) = 0.607( = {{\text{e}}^{ – 0.5}})\) A2
Note: Do not award this A1 for also stating (0.5, 0.607) as a coordinate.
EITHER
Correctly labelled graph of \(f'(x)\) for \(x < 0\) denoting the maximum \(f'(x)\) R1
(e.g. \(f'( – 0.6) = 1.17\) and \(f'( – 0.4) = 1.16\) stated) A1 N2
OR
Correctly labelled graph of \(f”(x)\) for \(x < 0\) denoting the maximum \(f'(x)\) R1
(e.g. \(f”( – 0.6) = 0.857\) and \(f”( – 0.4) = – 1.05\) stated) A1 N2
OR
\(f'(0.5) \approx 1.21\). \(f'(x) < 1.21\) just to the left of \(x = – \frac{1}{2}\)
and \(f'(x) < 1.21\) just to the right of \(x = – \frac{1}{2}\) R1
(e.g. \(f'( – 0.6) = 1.17\) and \(f'( – 0.4) = 1.16\) stated) A1 N2
OR
\(f”(x) > 0\) just to the left of \(x = – \frac{1}{2}\) and \(f”(x) < 0\) just to the right of \(x = – \frac{1}{2}\) R1
(e.g. \(f”( – 0.6) = 0.857\) and \(f”( – 0.4) = – 1.05\) stated) A1 N2
[7 marks]
METHOD 2
\(f'(x) = – 4x{{\text{e}}^{ – 2{x^2}}}\) A1
\(f”(x) = – 4{{\text{e}}^{ – 2{x^2}}} + 16{x^2}{{\text{e}}^{ – 2{x^2}}}\,\,\,\,\,\left( { = (16{x^2} – 4){{\text{e}}^{ – 2{x^2}}}} \right)\) A1
Attempting to solve \(f”(x) = 0\) (M1)
\(x = – \frac{1}{2}\) A1
Note: Do not award this A1 for stating \(x = \pm \frac{1}{2}\) as the final answer for x .
\(f\left( { – \frac{1}{2}} \right) = \frac{1}{{\sqrt {\text{e}} }}{\text{ }}( = 0.607)\) A1
Note: Do not award this A1 for also stating \(\left( {\frac{1}{2},\frac{1}{{\sqrt {\text{e}} }}} \right)\) as a coordinate.
EITHER
Correctly labelled graph of \(f'(x)\) for \(x < 0\) denoting the maximum \(f'(x)\) R1
(e.g. \(f'( – 0.6) = 1.17\) and \(f'( – 0.4) = 1.16\) stated) A1 N2
OR
Correctly labelled graph of \(f”(x)\) for \(x < 0\) denoting the maximum \(f'(x)\) R1
(e.g. \(f”( – 0.6) = 0.857\) and \(f”( – 0.4) = – 1.05\) stated) A1 N2
OR
\(f'(0.5) \approx 1.21\). \(f'(x) < 1.21\) just to the left of \(x = – \frac{1}{2}\)
and \(f'(x) < 1.21\) just to the right of \(x = – \frac{1}{2}\) R1
(e.g. \(f'( – 0.6) = 1.17\) and \(f'( – 0.4) = 1.16\) stated) A1 N2
OR
\(f”(x) > 0\) just to the left of \(x = – \frac{1}{2}\) and \(f”(x) < 0\) just to the right of \(x = – \frac{1}{2}\) R1
(e.g. \(f”( – 0.6) = 0.857\) and \(f”( – 0.4) = – 1.05\) stated) A1 N2
[7 marks]
Examiners report
Most candidates adopted an algebraic approach rather than a graphical approach. Most candidates found \(f'(x)\) correctly, however when attempting to find \(f”(x)\), a surprisingly large number either made algebraic errors using the product rule or seemingly used an incorrect form of the product rule. A large number ignored the domain restriction and either expressed \(x = \pm \frac{1}{2}\) as the x-coordinates of the point of inflection or identified \(x = \frac{1}{2}\) rather than \(x = – \frac{1}{2}\). Most candidates were unsuccessful in their attempts to justify the existence of the point of inflection.
Question
The function f is defined by \(f(x) = x\sqrt {9 – {x^2}} + 2\arcsin \left( {\frac{x}{3}} \right)\).
(a) Write down the largest possible domain, for each of the two terms of the function, f , and hence state the largest possible domain, D , for f .
(b) Find the volume generated when the region bounded by the curve y = f(x) , the x-axis, the y-axis and the line x = 2.8 is rotated through \(2\pi \) radians about the x-axis.
(c) Find \(f'(x)\) in simplified form.
(d) Hence show that \(\int_{ – p}^p {\frac{{11 – 2{x^2}}}{{\sqrt {9 – {x^2}} }}} {\text{d}}x = 2p\sqrt {9 – {p^2}} + 4\arcsin \left( {\frac{p}{3}} \right)\), where \(p \in D\) .
(e) Find the value of p which maximises the value of the integral in (d).
(f) (i) Show that \(f”(x) = \frac{{x(2{x^2} – 25)}}{{{{(9 – {x^2})}^{\frac{3}{2}}}}}\).
(ii) Hence justify that f(x) has a point of inflexion at x = 0 , but not at \(x = \pm \sqrt {\frac{{25}}{2}} \) .
▶️Answer/Explanation
Markscheme
(a) For \(x\sqrt {9 – {x^2}} \), \( – 3 \leqslant x \leqslant 3\) and for \(2\arcsin \left( {\frac{x}{3}} \right)\), \( – 3 \leqslant x \leqslant 3\) A1
\( \Rightarrow D{\text{ is }} – 3 \leqslant x \leqslant 3\) A1
[2 marks]
(b) \(V = \pi \int_0^{2.8} {{{\left( {x\sqrt {9 – {x^2}} = 2\arcsin \frac{x}{3}} \right)}^2}{\text{d}}x} \) M1A1
= 181 A1
[3 marks]
(c) \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = {(9 – {x^2})^{\frac{1}{2}}} – \frac{{{x^2}}}{{{{(9 – {x^2})}^{\frac{1}{2}}}}} + \frac{{\frac{2}{3}}}{{\sqrt {1 – \frac{{{x^2}}}{9}} }}\) M1A1
\( = {(9 – {x^2})^{\frac{1}{2}}} – \frac{{{x^2}}}{{{{(9 – {x^2})}^{\frac{1}{2}}}}} + \frac{2}{{{{(9 – {x^2})}^{\frac{1}{2}}}}}\) A1
\( = \frac{{9 – {x^2} – {x^2} + 2}}{{{{(9 – {x^2})}^{\frac{1}{2}}}}}\) A1
\( = \frac{{11 – 2{x^2}}}{{\sqrt {9 – {x^2}} }}\) A1
[5 marks]
(d) \(\int_{ – p}^p {\frac{{11 – 2{x^2}}}{{\sqrt {9 – {x^2}} }}{\text{d}}x = \left[ {x\sqrt {9 – {x^2}} + 2\arcsin \frac{x}{3}} \right]_{ – p}^p} \) M1
\( = p\sqrt {9 – {p^2}} + 2\arcsin \frac{p}{3} + p\sqrt {9 – {p^2}} + 2\arcsin \frac{p}{3}\) A1
\( = 2p\sqrt {9 – {p^2}} + 4\arcsin \left( {\frac{p}{3}} \right)\) AG
[2 marks]
(e) \(11 – 2{p^2} = 0\) M1
\(p = 2.35\,\,\,\,\,\left( {\sqrt {\frac{{11}}{2}} } \right)\) A1
Note: Award A0 for \(p = \pm 2.35\) .
[2 marks]
(f) (i) \(f”(x) = \frac{{{{(9 – {x^2})}^{\frac{1}{2}}}( – 4x) + x(11 – 2{x^2}){{(9 – {x^2})}^{ – \frac{1}{2}}}}}{{9 – {x^2}}}\) M1A1
\( = \frac{{ – 4x(9 – {x^2}) + x(11 – 2{x^2})}}{{{{(9 – {x^2})}^{\frac{3}{2}}}}}\) A1
\( = \frac{{ – 36x + 4{x^3} + 11x – 2{x^3}}}{{{{(9 – {x^2})}^{\frac{3}{2}}}}}\) A1
\( = \frac{{x(2{x^2} – 25)}}{{{{(9 – {x^2})}^{\frac{3}{2}}}}}\) AG
(ii) EITHER
When \(0 < x < 3\), \(f”(x) < 0\). When \( – 3 < x < 0\), \(f”(x) > 0\). A1
OR
\(f”(0) = 0\) A1
THEN
Hence \(f”(x)\) changes sign through x = 0 , giving a point of inflexion. R1
EITHER
\(x = \pm \sqrt {\frac{{25}}{2}} \) is outside the domain of f. R1
OR
\(x = \pm \sqrt {\frac{{25}}{2}} \) is not a root of \(f”(x) = 0\) . R1
[7 marks]
Total [21 marks]
Examiners report
It was disappointing to note that some candidates did not know the domain for arcsin. Most candidates knew what to do in (b) but sometimes the wrong answer was obtained due to the calculator being in the wrong mode. In (c), the differentiation was often disappointing with \(\arcsin \left( {\frac{x}{3}} \right)\) causing problems. In (f)(i), some candidates who failed to do (c) guessed the correct form of \(f'(x)\) (presumably from (d)) and then went on to find \(f”(x)\) correctly. In (f)(ii), the justification of a point of inflexion at x = 0 was sometimes incorrect – for example, some candidates showed simply that \(f'(x)\) is positive on either side of the origin which is not a valid reason.
Question
Let \(f(x) = \frac{{a + b{{\text{e}}^x}}}{{a{{\text{e}}^x} + b}}\), where \(0 < b < a\).
(a) Show that \(f'(x) = \frac{{({b^2} – {a^2}){{\text{e}}^x}}}{{{{(a{{\text{e}}^x} + b)}^2}}}\).
(b) Hence justify that the graph of f has no local maxima or minima.
(c) Given that the graph of f has a point of inflexion, find its coordinates.
(d) Show that the graph of f has exactly two asymptotes.
(e) Let a = 4 and b =1. Consider the region R enclosed by the graph of \(y = f(x)\), the y-axis and the line with equation \(y = \frac{1}{2}\).
Find the volume V of the solid obtained when R is rotated through \(2\pi \) about the x-axis.
▶️Answer/Explanation
Markscheme
(a) \(f'(x) = \frac{{b{{\text{e}}^x}(a{{\text{e}}^x} + b) – a{{\text{e}}^x}(a + b{{\text{e}}^x})}}{{{{(a{{\text{e}}^x} + b)}^2}}}\) M1A1
\( = \frac{{ab{{\text{e}}^{2x}} + {b^2}{{\text{e}}^x} – {a^2}{{\text{e}}^x} – ab{{\text{e}}^{2x}}}}{{{{(a{{\text{e}}^x} + b)}^2}}}\) A1
\( = \frac{{({b^2} – {a^2}){{\text{e}}^x}}}{{{{(a{{\text{e}}^x} + b)}^2}}}\) AG
[3 marks]
(b) EITHER
\(f'(x) = 0 \Rightarrow ({b^2} – {a^2}){{\text{e}}^x} = 0 \Rightarrow b = \pm a{\text{ or }}{{\text{e}}^x} = 0\) A1
which is impossible as \(0 < b < a\) and \({{\text{e}}^x} > 0\) for all \(x \in \mathbb{R}\) R1
OR
\(f'(x) < 0\) for all \(x \in \mathbb{R}\) since \(0 < b < a\) and \({{\text{e}}^x} > 0\) for all \(x \in \mathbb{R}\) A1R1
OR
\(f'(x)\) cannot be equal to zero because \({{\text{e}}^x}\) is never equal to zero A1R1
[2 marks]
(c) EITHER
\(f”(x) = \frac{{({b^2} – {a^2}){{\text{e}}^x}{{(a{{\text{e}}^x} + b)}^2} – 2a{{\text{e}}^x}(a{{\text{e}}^x} + b)({b^2} – {a^2}){{\text{e}}^x}}}{{{{(a{{\text{e}}^x} + b)}^4}}}\) M1A1A1
Note: Award A1 for each term in the numerator.
\( = \frac{{({b^2} – {a^2}){{\text{e}}^x}(a{{\text{e}}^x} + b – 2a{{\text{e}}^x})}}{{{{(a{{\text{e}}^x} + b)}^3}}}\)
\( = \frac{{({b^2} – {a^2})(b – a{{\text{e}}^x}){{\text{e}}^x}}}{{{{(a{{\text{e}}^x} + b)}^3}}}\)
OR
\(f'(x) = ({b^2} – {a^2}){{\text{e}}^x}{(a{{\text{e}}^x} + b)^{ – 2}}\)
\(f”(x) = ({b^2} – {a^2}){{\text{e}}^x}{(a{{\text{e}}^x} + b)^{ – 2}} + ({b^2} – {a^2}){{\text{e}}^x}( – 2a{{\text{e}}^x}){(a{{\text{e}}^x} + b)^{ – 3}}\) M1A1A1
Note: Award A1 for each term.
\( = ({b^2} – {a^2}){{\text{e}}^x}{(a{{\text{e}}^x} + b)^{ – 3}}\left( {(a{{\text{e}}^x} + b) – 2a{{\text{e}}^x}} \right)\)
\( = ({b^2} – {a^2}){{\text{e}}^x}{(a{{\text{e}}^x} + b)^{ – 3}}(b – a{{\text{e}}^x})\)
THEN
\(f”(x) = 0 \Rightarrow b – a{{\text{e}}^x} = 0 \Rightarrow x = \ln \frac{b}{a}\) M1A1
\(f\left( {\ln \frac{b}{a}} \right) = \frac{{{a^2} + {b^2}}}{{2ab}}\) A1
coordinates are \(\left( {\ln \frac{b}{a},\frac{{{a^2} + {b^2}}}{{2ab}}} \right)\)
[6 marks]
(d) \(\mathop {\lim }\limits_{x – \infty } f(x) = \frac{a}{b} \Rightarrow y = \frac{a}{b}\) horizontal asymptote A1
\(\mathop {\lim }\limits_{x \to + \infty } f(x) = \frac{b}{a} \Rightarrow y = \frac{b}{a}\) horizontal asymptote A1
\(0 < b < a \Rightarrow a{{\text{e}}^x} + b > 0\) for all \(x \in \mathbb{R}\) (accept \(a{{\text{e}}^x} + b \ne 0\))
so no vertical asymptotes R1
Note: Statement on vertical asymptote must be seen for R1.
[3 marks]
(e) \(y = \frac{{4 + {{\text{e}}^x}}}{{4{{\text{e}}^x} + 1}}\)
\(y = \frac{1}{2} \Leftrightarrow x = \ln \frac{7}{2}\) (or 1.25 to 3 sf) (M1)(A1)
\(V = \pi \int_0^{\ln \frac{7}{2}} {\left( {{{\left( {\frac{{4 + {{\text{e}}^x}}}{{4{{\text{e}}^x} + 1}}} \right)}^2} – \frac{1}{4}} \right){\text{d}}x} \) (M1)A1
\( = 1.09\) (3 sf) A1 N4
[5 marks]
Total [19 marks]
Examiners report
This question was well attempted by many candidates. In some cases, candidates who skipped other questions still answered, with some success, parts of this question. Part (a) was in general well done but in (b) candidates found difficulty in justifying that f’(x) was non-zero. Performance in part (c) was mixed: it was pleasing to see good levels of algebraic ability of good candidates who successfully answered this question; weaker candidates found the simplification required difficult. There were very few good answers to part (d) which showed the weaknesses of most candidates in dealing with the concept of asymptotes. In part (e) there were a large number of good attempts, with many candidates evaluating correctly the limits of the integral and a smaller number scoring full marks in this part.
