Question
[Maximum mark: 8]
(a) Write down the first three terms of the binomial expansion of \(\left ( 1+t \right )^{-1}\) in ascending powers of t. [1]
(b) By using the Maclaurin series for \(\cos x\) and the result from part (a), show that the Maclaurin series for \(\sec x\) up to and including the term in \( x^{4}\) \(+\frac{x^{2}}{2}+\frac{5x^{4}}{24} \) [4]
(c) By using the Maclaurin series for \(\arctan x \) and the result from part (b), find \(\lim_{x\rightarrow 0}\left ( \frac{\arctan2x}{\sec x-1} \right )\). [3]
▶️Answer/Explanation

Question
Consider the expansion of \((3+x^2)^{n+1}\), where \(n\in \mathbb{Z}^+\)
Given that the coefficient of x4 is 20412, find the value of n .
▶️Answer/Explanation
Ans:
METHOD 1
product of a binomial coefficient, a power of 3 (and a power of x2 ) seen evidence of correct term chosen
n+1C2 × 3n+1−2 ×(x2)2 =\((\frac{n(n+1)}{2}\times 3^{n-1}\times x^{4})\)
OR
n-r = 1
equating their coefficient to 20412 or their term to 20142x4
EITHER
n+1C2 × 3n-1 = 20412
OR
r+2C2 × 3r = 20142 ⇒ r = 6
THEN
n =7
METHOD 2
\(3^{n+1}(1+\frac{x^{2}}{3})^{n+1}\)
product of a binomial coefficient and a power of \(\frac{x^2}{3}\) OR \(\frac{1}{3}\) evidence of correct term chosen
3n+1×n+1C2 \((\frac{x^{2}}{3})^2\)
=\((\frac{n(n+1)}{2}\times 3^{n-1}\times x^{4})\)
equating their coefficient to 20412 or their term to 20412x4
\(3^{n-1}\times \frac{n(n+1)}{2}\)= 20412
n= 7
Question
Find the term independent of x in the expansion of \(\frac{1}{x^3}(\frac{1}{3x^2-\frac{x}{2}})^9\)
▶️Answer/Explanation
Ans:
use of Binomial expansion to find a term in either
\((\frac{1}{3x^{2}}-\frac{x}{2})^{2}\), \((\frac{1}{3}-\frac{x^{2}}{3})^{9},(\frac{1}{3x^{2}}-\frac{1}{2})^{9} or (2-3x^{3})\)
finding the powers required to be 2 and 7 constant term is 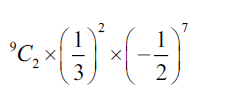
therefore term independent of x is \(-\frac{1}{32}(=-0.03125)\)
Question
Find the constant term in the expansion of \({\left( {x – \frac{2}{x}} \right)^4}{\left( {{x^2} + \frac{2}{x}} \right)^3}\).
▶️Answer/Explanation
Markscheme
\({\left( {x – \frac{2}{x}} \right)^4} = {x^4} – 8{x^2} + 24 – \frac{{32}}{{{x^2}}} + \frac{{16}}{{{x^4}}}\) (M1)(A1)
\({\left( {{x^2} + \frac{2}{x}} \right)^3} = {x^6} + 6{x^3} + 12 + \frac{8}{{{x^3}}}\) (M1)(A1)
Note: Accept unsimplified or uncalculated coefficients in the constant term
\( = 24 \times 12\) (M1)(A1)
\( = 288\) A1
[7 marks]
Examiners report
Many correct answers were seen, although most candidates used rather inefficient methods (e.g. expanding the brackets in multiple steps). In a very few cases candidates used the binomial theorem to obtain the answer quickly.
Question
Determine the first three terms in the expansion of \({(1 – 2x)^5}{(1 + x)^7}\) in ascending powers of x.
▶️Answer/Explanation
Markscheme
METHOD 1
constant term: \(\left( {\begin{array}{*{20}{c}}
5 \\
0
\end{array}} \right){( – 2x)^0}\left( {\begin{array}{*{20}{c}}
7 \\
0
\end{array}} \right){x^0} = 1\) A1
term in x: \(\left( {\begin{array}{*{20}{c}}
7 \\
1
\end{array}} \right)x + \left( {\begin{array}{*{20}{c}}
5 \\
1
\end{array}} \right)( – 2x) = – 3x\) (M1)A1
term in \({x^2}\) : \(\left( {\begin{array}{*{20}{c}}
7 \\
2
\end{array}} \right){x^2} + \left( {\begin{array}{*{20}{c}}
5 \\
2
\end{array}} \right){( – 2x)^2} + \left( {\begin{array}{*{20}{c}}
7 \\
1
\end{array}} \right)x\left( {\begin{array}{*{20}{c}}
5 \\
1
\end{array}} \right)( – 2x) = – 9{x^2}\) M1A1 N3
[5 marks]
METHOD 2
\({(1 – 2x)^5}{(1 + x)^7} = \left( {1 + 5( – 2x) + \frac{{5 \times 4{{( – 2x)}^2}}}{{2!}} + …} \right)\left( {1 + 7x + \frac{{7 \times 6}}{2}{x^2} + …} \right)\) M1M1
\( = (1 – 10x + 40{x^2} + …)(1 + 7x + 21{x^2} + …)\)
\( = 1 + 7x + 21{x^2} – 10x – 70{x^2} + 40{x^2} + …\)
\( = 1 – 3x – 9{x^2} + …\) A1A1A1 N3
[5 marks]
Examiners report
Although the majority of the candidates understood the question and attempted it, excessive time was spent on actually expanding the expression without consideration of the binomial theorem. A fair amount of students confused “ascending order”, giving the last three instead of the first three terms.
Question
When \((1+\frac{x}{2})^n\), n\(\epsilon \mathbb{N}\), is expanded in ascending powers of x, the coefficient of x3 is 70.
(a) Find the value of n.
(b) Hence, find the coefficient of x2.
▶️Answer/Explanation
Ans
(a) coefficient of x3 is \(\begin{pmatrix}n\\3\end{pmatrix}(\frac{1}{2})^3=70\)
\(\frac{n!}{3!(n-3)!}\chi \frac{1}{8}=70\)
\(\Rightarrow \frac{n(n-1)(n-2)}{48}=70\)
n = 16
(b) \(\begin{pmatrix}16\\2\end{pmatrix}(\frac{1}{2})^2=30\)
