Question
Let y = \(\frac{Inx}{x^{4}}\) for x > 0.
(a) Show that \(\frac{dy}{dx}= \frac{1-4Inx}{x^{5}}\)
Consider the function defined by f (x) \(\frac{Inx}{x^{4}}\) = for x> 0 and its graph y = f (x) .
(b) The graph of f has a horizontal tangent at point P. Find the coordinates of P. [5]
(c) Given that f ” (x) = \(\frac{20Lnx-9}{x^{6}}\) show that P is a local maximum point. [3]
(d) Solve f (x) > 0 for x > 0. [2]
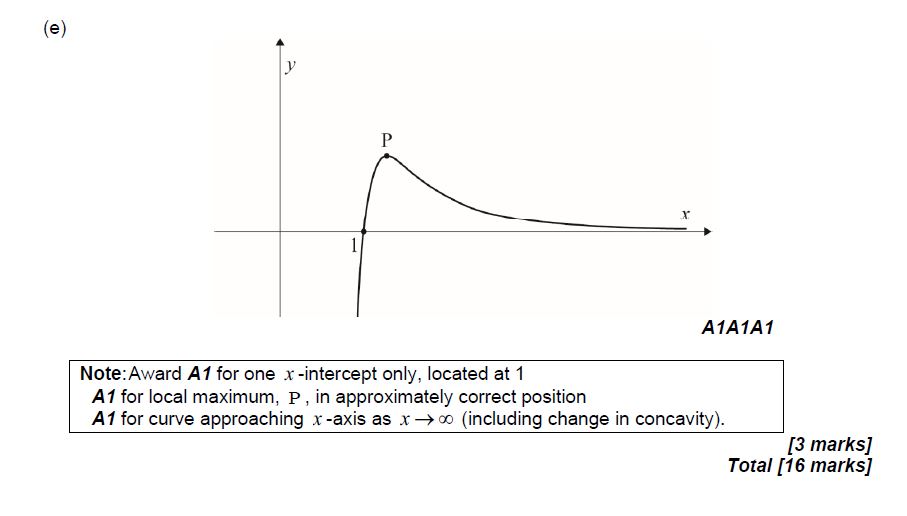
(e) Sketch the graph of f , showing clearly the value of the x-intercept and the approximate position of point P. [3]
Answer/Explanation
Ans



Question
Let \(f(x) = {{\rm{e}}^{ – 3x}}\) and \(g(x) = \sin \left( {x – \frac{\pi }{3}} \right)\) .
Write down
(i) \(f'(x)\) ;
(ii) \(g'(x)\) .
Let \(h(x) = {{\rm{e}}^{ – 3x}}\sin \left( {x – \frac{\pi }{3}} \right)\) . Find the exact value of \(h’\left( {\frac{\pi }{3}} \right)\) .
Answer/Explanation
Markscheme
(i) \( – 3{{\rm{e}}^{ – 3x}}\) A1 N1
(ii) \(\cos \left( {x – \frac{\pi }{3}} \right)\) A1 N1
[4 marks]
evidence of choosing product rule (M1)
e.g. \(uv’ + vu’\)
correct expression A1
e.g. \( – 3{{\rm{e}}^{ – 3x}}\sin \left( {x – \frac{\pi }{3}} \right) + {{\rm{e}}^{ – 3x}}\cos \left( {x – \frac{\pi }{3}} \right)\)
complete correct substitution of \(x = \frac{\pi }{3}\) (A1)
e.g. \( – 3{{\rm{e}}^{ – 3\frac{\pi }{3}}}\sin \left( {\frac{\pi }{3} – \frac{\pi }{3}} \right) + {{\rm{e}}^{ – 3\frac{\pi }{3}}}\cos \left( {\frac{\pi }{3} – \frac{\pi }{3}} \right)\)
\(h’\left( {\frac{\pi }{3}} \right) = {{\rm{e}}^{ – \pi }}\) A1 N3
[4 marks]
Question
Consider \(f(x) = {x^2} + \frac{p}{x}\) , \(x \ne 0\) , where p is a constant.
Find \(f'(x)\) .
There is a minimum value of \(f(x)\) when \(x = – 2\) . Find the value of \(p\) .
Answer/Explanation
Markscheme
\(f'(x) = 2x – \frac{p}{{{x^2}}}\) A1A1 N2
Note: Award A1 for \(2x\) , A1 for \( – \frac{p}{{{x^2}}}\) .
[2 marks]
evidence of equating derivative to 0 (seen anywhere) (M1)
evidence of finding \(f'( – 2)\) (seen anywhere) (M1)
correct equation A1
e.g. \( – 4 – \frac{p}{4} = 0\) , \( – 16 – p = 0\)
\(p = – 16\) A1 N3
[4 marks]
Question
Let \(f(x) = p{x^3} + p{x^2} + qx\).
Find \(f'(x)\).
Given that \(f'(x) \geqslant 0\), show that \({p^2} \leqslant 3pq\).
Answer/Explanation
Markscheme
\(f'(x) = 3p{x^2} + 2px + q\) A2 N2
Note: Award A1 if only 1 error.
[2 marks]
evidence of discriminant (must be seen explicitly, not in quadratic formula) (M1)
eg \({b^2} – 4ac\)
correct substitution into discriminant (may be seen in inequality) A1
eg \({(2p)^2} – 4 \times 3p \times q,{\text{ }}4{p^2} – 12pq\)
\(f'(x) \geqslant 0\) then \(f’\) has two equal roots or no roots (R1)
recognizing discriminant less or equal than zero R1
eg \(\Delta \leqslant 0,{\text{ }}4{p^2} – 12pq \leqslant 0\)
correct working that clearly leads to the required answer A1
eg \({p^2} – 3pq \leqslant 0,{\text{ }}4{p^2} \leqslant 12pq\)
\({p^2} \leqslant 3pq\) AG N0
[5 marks]
Question
Consider the function \(f(t)=3\sec ^{2}t+5t\). Find (a) \(f'(t)\). (b) (ⅰ) \(f(\pi )\); (ⅱ) \(f'(\pi )\);
Answer/Explanation
Ans
(a) METHOD 1
\(f(t)=3\sec ^{2}t+5t=3(\cos t)^{-2}+5t\)
\(f(t)=-6(\cos t)^{-3}(-\sin t)+5=\frac{6\sin t}{cos^{3}t}+5\)
METHOD 2
\(f'(t)=3\times 2\sec t(\sec t\tan t)+5\)
\(=6\sec ^{2}t \tan t+5(=6\tan ^{2}t+6 \tan t+5)\)
(b) \(f(\pi )=\frac{3}{(\cos \pi )^{2}}+5\pi =3+5\pi\)
\(f'(\pi )=\frac{6\sin \pi }{(\cos \pi )^{3}}+5=5\)
