Question
The equation of the line y = mx + c can be expressed in vector form r = a + \(\lambda b\).
(a) Find the vectors a and b in terms of m and/or c.
The matrix M is defined by \(\begin{pmatrix}
6 &3 \\
4& 2
\end{pmatrix}\)
(b) Find the value of det M.
The line y = mx + c (where \(m \neq – 2)\) is transformed into a new line using the transformation described by matrix M.
(c) Show that the equation of the resulting line does not depend on m or c.
▶️Answer/Explanation
Ans:
(a) (one vector to the line is \(\binom{1}{m}\) therefore) a= (\(\binom{0}{c} \)
the line goes m up for every 1 across
(so the direction vector is) \(b= ( \binom{1}{m}\)
(b) (from GDC OR \(6 \times 2 – 4 \times 3) \) |M| = 0
(c) METHOD 1
\(\binom{X}{Y} = \begin{pmatrix}
6 & 3\\
4 & 2
\end{pmatrix} \binom{x}{mx+c}= \binom{6x + 3mx + 3c}{4x + 2mx + 2c}\)
therefore the new line has equation 3Y = 2X
which is independent of m or c
METHOD 2
take two points on the line, e.g. (0, c) and (1, m+c)
these map to \(\begin{pmatrix}
6 & 3\\
4 & 2
\end{pmatrix}\binom{0}{c}=\binom{3c}{2c}\)
and \(\begin{pmatrix}
6 & 3\\
4 & 2
\end{pmatrix}\binom{1}{m+c}=\binom{6+3m+3c}{4+2m+2c}\)
therefore a direction vector is \(\binom{6+3m}{4+2m}=(2+m)\binom{3}{2}\)
(since \(\neq -2\)) a direction vector is \(\binom{3}{2}\)
the line passes through \(\binom{3c}{2c})-c \biniom{3}{2} = \binom{0}{0}\) therefore it always has the
origin as a jump-on vector
the vector equation is therefore \(r=\mu \binom{3}{2}\)
which is independent of m or c
METHOD 3
\(r=\begin{pmatrix}
6 & 3\\
4 & 2
\end{pmatrix}(\binom{0}{c}+ \lambda \binom{1}{m})=\binom{3c}{2c}+ \lambda \binom{6+3m}{4+2m}\)
\(=c \binom{3}{2}+(2+m)\lambda \binom{3}{2}\)
\(=\mu \binom{3}{2}\)
where \(\mu=c+(2+m) \lambda\) is an arbitrary parameter.
which is independent of m or c (as \(\mu\) can take any value)
Question
The matrix M is given by
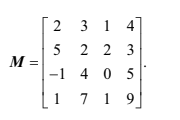
Justifying your answer, determine the rank of M . [3]
Let the set S =
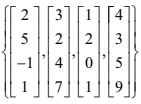that is the four columns of M.Give a reason why S does not span the space of four-dimensional column vectors. [1]
Determine whether the vector
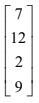belongs to the subspace spanned by S . [3]
▶️Answer/Explanation
Ans:
(a)
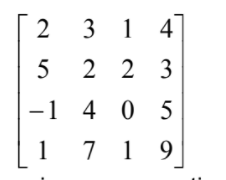
using row operations, the matrix becomes for example
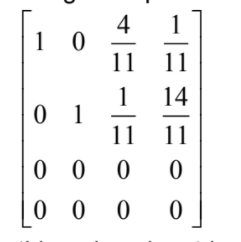
this reduced matrix contains 2 independent rows so the rank of M is 2
(b)
in order to span the space of 4-D column vectors, the 4 vectors in S would have to be independent so the rank of M would have to be 4 which it is not
(c)
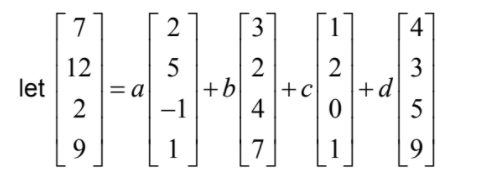
attempting to solve on GDC, we find that there is an infinite number of solutions therefore the given vector does belong to the subspace spanned by S
Question
The matrix A is given by A = \(\left( {\begin{array}{*{20}{c}}1&2&1\\1&1&2\\2&3&1\end{array}} \right)\).
(a) Given that A\(^3\) can be expressed in the form A\(^3 = a\)A\(^2 = b\)A \( + c\)I, determine the values of the constants \(a\), \(b\), \(c\).
(b) (i) Hence express A\(^{ – 1}\) in the form A\(^{ – 1} = d\)A\(^2 = e\)A \( + f\)I where \(d,{\text{ }}e,{\text{ }}f \in \mathbb{Q}\).
(ii) Use this result to determine A\(^{ – 1}\).
▶️Answer/Explanation
Markscheme
(a) successive powers of A are given by
A\(^2 = \) \(\left( {\begin{array}{*{20}{c}}5&7&6\\6&9&5\\7&{10}&9\end{array}} \right)\) (M1)A1
A\(^3 = \) \(\left( {\begin{array}{*{20}{c}}{24}&{35}&{25}\\{25}&{36}&{29}\\{35}&{51}&{36}\end{array}} \right)\) A1
it follows, considering elements in the first rows, that
\(5a + b + c = 24\)
\(7a + 2b = 35\)
\(6a + b = 25\) M1A1
solving, (M1)
\((a,{\text{ }}b,{\text{ }}c) = (3,{\text{ }}7,{\text{ }}2)\) A1
Note: Accept any other three correct equations.
Note: Accept the use of the Cayley–Hamilton Theorem.
[7 marks]
(b) (i) it has been shown that
A\(^3 = 3\)A\(^2 + 7\)A\( + 2\)I
multiplying by A\(^{ – 1}\), M1
A\(^2 = 3\)A\( + 7\)I\( + 2\)A\(^{ – 1}\) A1
whence
A\(^{ – 1} = 0.5\)A\(^2 – 1.5\)A \( – 3.5\)I A1
(ii) substituting powers of A,
A\(^{ – 1} = 0.5\)\(\left( {\begin{array}{*{20}{c}}5&7&6\\6&9&5\\7&{10}&9\end{array}} \right) – 1.5\left( {\begin{array}{*{20}{c}}1&2&1\\1&1&2\\2&3&1\end{array}} \right) – 3.5\left( {\begin{array}{*{20}{c}}1&0&0\\0&1&0\\0&0&1\end{array}} \right)\) M1
=\(\left( {\begin{array}{*{20}{c}}{ – 2.5}&{0.5}&{1.5}\\{1.5}&{ – 0.5}&{ – 0.5}\\{0.5}&{0.5}&{ – 0.5}\end{array}} \right)\) A1
Note: Follow through their equation in (b)(i).
Note: Line (ii) of (ii) must be seen.
[5 marks]
Question
A matrix M is called idempotent if M\(^2 = \) M.
The idempotent matrix N has the form
N \( = \left( {\begin{array}{*{20}{c}} a&{ – 2a} \\ a&{ – 2a} \end{array}} \right)\)
where \(a \ne 0\).
a.(i) Explain why M is a square matrix.
(ii) Find the set of possible values of det(M).[4]
b.(i) Find the value of \(a\).
(ii) Find the eigenvalues of N.
(iii) Find corresponding eigenvectors.[12]
▶️Answer/Explanation
Markscheme
(i) M\(^2 = \) MM only exists if the number of columns of M equals the number of rows of M R1
hence M is square AG
(ii) apply the determinant function to both sides M1
\(\det (\)M\(^2) = \det (\)M\()\)
use the multiplicative property of the determinant
\(\det (\)M\(^2) = \det (\)M\(){\text{ }}\det (\)M\() = \det (\)M\()\) (M1)
hence \(\det (\)M\() = 0\) or 1 A1
[4 marks]
(i) attempt to calculate N\(^2\) M1
obtain \(\left( {\begin{array}{*{20}{c}} { – {a^2}}&{2{a^2}} \\ { – {a^2}}&{2{a^2}} \end{array}} \right)\) A1
equating to N M1
to obtain \(a = – 1\) A1
(ii) N \( = \left( {\begin{array}{*{20}{c}} { – 1}&2 \\ { – 1}&2 \end{array}} \right)\)
N \( – \lambda \)I \( = \left( {\begin{array}{*{20}{c}} { – 1 – \lambda }&2 \\ { – 1}&{2 – \lambda } \end{array}} \right)\) M1
\(( – 1 – \lambda )(2 – \lambda ) + 2 = 0\) (A1)
\({\lambda ^2} – \lambda = 0\) (A1)
\(\lambda \) is 1 or 0 A1
(iii) let \(\lambda = 1\)
to obtain \(\left( {\begin{array}{*{20}{c}} { – 1}&2 \\ { – 1}&2 \end{array}} \right)\left( {\begin{array}{*{20}{c}} x \\ y \end{array}} \right) = \left( {\begin{array}{*{20}{c}} x \\ y \end{array}} \right){\text{ or }}\left( {\begin{array}{*{20}{c}} { – 2}&2 \\ { – 1}&1 \end{array}} \right)\left( {\begin{array}{*{20}{c}} x \\ y \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 0 \\ 0 \end{array}} \right)\) M1
hence eigenvector is \(\left( {\begin{array}{*{20}{c}} x \\ x \end{array}} \right)\) A1
let \(\lambda = 0\)
to obtain \(\left( {\begin{array}{*{20}{c}} { – 1}&2 \\ { – 1}&2 \end{array}} \right)\left( {\begin{array}{*{20}{c}} x \\ y \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 0 \\ 0 \end{array}} \right)\) M1
hence eigenvector is \(\left( {\begin{array}{*{20}{c}} {2y} \\ y \end{array}} \right)\) A1
Note: Accept specific eigenvectors.
[12 marks]
Question
Let A2 = 2A + I where A is a 2 × 2 matrix.
a.Show that A4 = 12A + 5I.[3]
b.Let B = \(\left[ {\begin{array}{*{20}{c}}
4&2 \\
1&{ – 3}
\end{array}} \right]\).
Given that B2 – B – 4I = \(\left[ {\begin{array}{*{20}{c}}
k&0 \\
0&k
\end{array}} \right]\), find the value of \(k\).[3]
▶️Answer/Explanation
Markscheme
METHOD 1
A4 = 4A2 + 4AI + I2 or equivalent M1A1
= 4(2A + I) + 4A + I A1
= 8A + 4I + 4A + I
= 12A + 5I AG
[3 marks]
METHOD 2
A3 = A(2A + I) = 2A2 + AI = 2(2A + I) + A(= 5A + 2I) M1A1
A4 = A(5A + 2I) A1
= 5A2 + 2A = 5(2A + I) + 2A
= 12A + 5I AG
[3 marks]
B2 = \(\left[ {\begin{array}{*{20}{c}}
{18}&2 \\
1&{11}
\end{array}} \right]\) (A1)
\(\left[ {\begin{array}{*{20}{c}}
{18}&2 \\
1&{11}
\end{array}} \right] – \left[ {\begin{array}{*{20}{c}}
4&2 \\
1&{ – 3}
\end{array}} \right] – \left[ {\begin{array}{*{20}{c}}
4&0 \\
0&4
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{10}&0 \\
0&{10}
\end{array}} \right]\) (A1)
\( \Rightarrow k = 10\) A1
[3 marks]