Question 4. [Maximum mark: 18]
In a small village there are two doctors’ clinics, one owned by Doctor Black and the other owned by Doctor Green. It was noted after each year that 3.5 % of Doctor Black’s patients moved to Doctor Green’s clinic and 5 % of Doctor Green’s patients moved to Doctor Black’s clinic. All additional losses and gains of patients by the clinics may be ignored.
At the start of a particular year, it was noted that Doctor Black had 2100 patients on their register, compared to Doctor Green’s 3500 patients.
a. Write down a transition matrix T indicating the annual population movement between clinics. [2]
b. Find a prediction for the ratio of the number of patients Doctor Black will have, compared to Doctor Green, after two years. [2]
c. Find a matrix P , with integer elements, such that T = PDP–1 , where D is a diagonal matrix.
d. Hence, show that the long-term transition matrix T x is given by T x =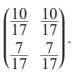 
e. Hence, or otherwise, determine the expected ratio of the number of patients Doctor Black would have compared to Doctor Green in the long term. [2]
▶️Answer/Explanation
(a) 
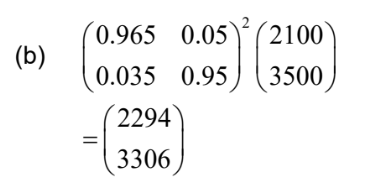so ratio is \(2294 : 3306 = (1147 :1653, 0.693889…)\)
(c) to solve Ax = λx :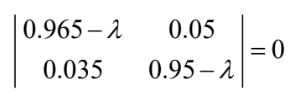 
\( (0.965 – λ) (0.95 – λ) -0.05 × 0.035 = 0\)
\(λ = 0.915 OR λ =1\)
attempt to find eigenvectors for at least one eigenvalue when \(λ = 0.915\) , \(x=(_{-1}^{1})\)
(or any real multiple) when λ =1, \(x=(_{7}^{10})\) therefore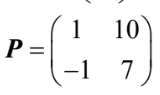 
(accept integer valued multiples of their eigenvectors and columns in either order) 
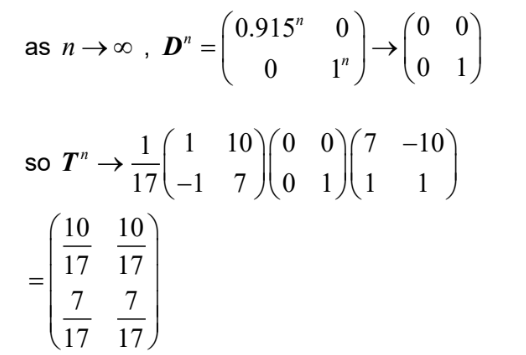
(e)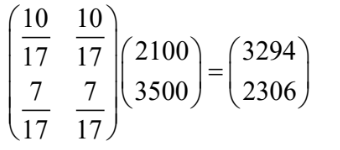 
so ratio is \(3294 : 2306\) \((1647 :1153, 1.42844…, 0.700060…)\)
Question 5. [Maximum mark: 13]
Long term experience shows that if it is sunny on a particular day in Vokram, then the probability that it will be sunny the following day is 0.8. If it is not sunny, then the probability that it will be sunny the following day is 0.3.
The transition matrix T is used to model this information, where T =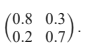 
a. It is sunny today. Find the probability that it will be sunny in three days’ time. [2]
b. Find the eigenvalues and eigenvectors of T . [5]
The matrix T can be written as a product of three matrices, PD P -1, where D is a diagonal matrix.
c.(i) Write down the matrix P .
c.(ii) Write down the matrix D . [2]
d. Hence find the long-term percentage of sunny days in Vokram. [4]
▶️Answer/Explanation
(a) finding T3 OR use of tree diagram T3 = 
the probability of sunny in three days’ time is 0.65
(b) attempt to find eigenvalues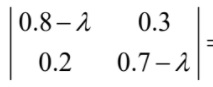 
\(= (0.8 \lambda )(0.7-\lambda )-0.06 = 0\) (\lambda ^{2}- 1.5 \lambda + 0.5= 0 \lambda =1, \lambda = 0.5)\)
attempt to find either eigenvector \(0.8+0.3y= x ⇒ -0.2x+ 0.3y= 0\) so an eigenvector is \((_{2}^{3})\)0.8x+ 0.3y = 0.5x ⇒ 0.3x+0.3y = 0\) so an eigenvector is \( _{1}^{-1}\)
(c) (i) P=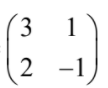 
OR P =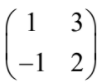 
(ii) D =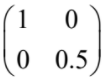 
OR D =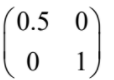 
(d) \(0.5n → 0\)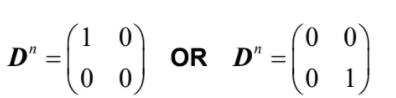 
PDnP-1 60 %
Question
A particle moves such that its displacement, x metres, from a point O at time t seconds
is given by the differential equation
\(\frac{d^2x}{dt^2}+5\frac{dx}{dt}+6x=0\)
(a) (i) use the substitution \(y = \frac{dx}{dt}\) to show that this equation can be written as
\(\binom{\frac{dx}{dt}}{\frac{dy}{dt}} = \begin{pmatrix}
0 & 1\\
-6 & -5
\end{pmatrix} \binom{x}{y}\)
(ii) Find the eigenvalues for the matrix \(\begin{pmatrix}
0 & 1\\
-6 & -5
\end{pmatrix}\)
(iii) Hence state the long-term velocity of the particle.
The equation for the motion of the particle is amended to
\(\frac{d^2x}{dt^2}+5 \frac{dx}{dt} +6x = 3t + 4\).
(b) (i) Use the substitution \(y = \frac{dx}{dt}\) to write the differential equation as a system of coupled, first order differential equations
When t = 0 the particle is stationary at O.
(ii) Use Euler’s method with a step length of 0.1 to find the displacement of the
particle when t = 1.
(iii) Find the long-term velocity of the particle.
▶️Answer/Explanation
Ans:
(a) (i) \(y=\frac{dx}{dy} \Rightarrow \frac{dy}{dt} + 5 \frac{dx}{dt}+ 6x = 0\) OR \(\frac{dy}{dt} + 5y + 6x = 0\)
\(\binom{\frac{dx}{dt}}{\frac{dy}{dt}} = \begin{pmatrix}
0 & 1\\
-6 & -5
\end{pmatrix}\binom{x}{y}\)
(ii) \(det\begin{pmatrix}
-\lambda & 1\\
-6 & -5-\lambda
\end{pmatrix}= 0\)
\(-\lambda (-5 – \lambda ) + 6 = 0\) OR \(\lambda^2 + 5 \lambda + 6 = 0\)
\(\lambda = -2, -3\)
(iii) (on a phase portrait teh particle approachs (0,0) as t increases so long term velocity (y) is )
(b) (i) \(y=\frac{dx}{dy}\)
\(\frac{d^2x}{dt^2}=\frac{dy}{dt}\)
\(\frac{dy}{dt}+5y + 6x = 3t + 4\)
(ii) recognition that h = 0.1 in any recurrence formula
\((t_{n+1}=t_n + 0.1)
\(x_{n+1} = x_n + 0.1y_n\)
\(y_{n+1}=y_n + 0.1(3t_n + 4 -5y_n – 6x_n)\)
(when t = 1,) x = 0.64402…\(\approx\) 0.644 m
(iii) recognizing that y is the velocity
0.5 \(ms^{-1}\)
Question
Given that the elements of a \(2 \times 2\) symmetric matrix are real, show that
(i) the eigenvalues are real;
(ii) the eigenvectors are orthogonal if the eigenvalues are distinct.[11]
The matrix \(\boldsymbol{A}\) is given by\[\boldsymbol{A} = \left( {\begin{array}{*{20}{c}}
{11}&{\sqrt 3 }\\
{\sqrt 3 }&9
\end{array}} \right) .\]Find the eigenvalues and eigenvectors of \(\boldsymbol{A}\).[7]
The ellipse \(E\) has equation \({{\boldsymbol{X}}^T}{\boldsymbol{AX}} = 24\) where \(\boldsymbol{X} = \left( \begin{array}{l}
x\\
y
\end{array} \right)\) and \(\boldsymbol{A}\) is as defined in part (b).
(i) Show that \(E\) can be rotated about the origin onto the ellipse \(E’\) having equation \(2{x^2} + 3{y^2} = 6\) .
(ii) Find the acute angle through which \(E\) has to be rotated to coincide with \(E’\) .[7]
▶️Answer/Explanation
Markscheme
(i) let \(\boldsymbol{M} = \left( {\begin{array}{*{20}{c}}
a&b\\
b&c
\end{array}} \right)\) (M1)
the eigenvalues satisfy
\(\det (\boldsymbol{M} – \lambda \boldsymbol{I}) = 0\) (M1)
\((a – \lambda )(c – \lambda ) – {b^2} = 0\) (A1)
\({\lambda ^2} – \lambda (a + c) + ac – {b^2} = 0\) A1
discriminant \( = {(a + c)^2} – 4(ac – {b^2})\) M1
\( = {(a – c)^2} + 4{b^2} \ge 0\) A1
this shows that the eigenvalues are real AG
(ii) let the distinct eigenvalues be \({\lambda _1},{\lambda _2}\) , with eigenvectors \({{\boldsymbol{X}}_1}\), \({{\boldsymbol{X}}_2}\)
then
\({\lambda _1}{{\boldsymbol{X}}_1} = {\boldsymbol{M}}{{\boldsymbol{X}}_1}\) and \({\lambda _2}{{\boldsymbol{X}}_2} = {\boldsymbol{M}}{{\boldsymbol{X}}_1}\) M1
transpose the first equation and postmultiply by \({{\boldsymbol{X}}_2}\) to give
\({\lambda _1}{\boldsymbol{X}}_1^T{{\boldsymbol{X}}_2} = {\boldsymbol{X}}_1^T{\boldsymbol{M}}{{\boldsymbol{X}}_2}\) A1
premultiply the second equation by \({\boldsymbol{X}}_1^T\)
\({\lambda _2}{\boldsymbol{X}}_1^T{{\boldsymbol{X}}_2} = {\boldsymbol{X}}_1^T{\boldsymbol{M}}{{\boldsymbol{X}}_2}\) A1
it follows that
\((\lambda 1 – {\lambda _2}){\boldsymbol{X}}_1^T{{\boldsymbol{X}}_2} = 0\) A1
since \(\lambda 1 \ne {\lambda _2}\) , it follows that \({\boldsymbol{X}}_1^T{{\boldsymbol{X}}_2} = 0\) so that the eigenvectors are orthogonal R1
[11 marks]
the eigenvalues satisfy \(\left| \begin{array}{l}
11 – \lambda \\
\sqrt 3
\end{array} \right.\left. \begin{array}{l}
\sqrt 3 \\
9 – \lambda
\end{array} \right| = 0\) M1A1
\({\lambda ^2} – 20\lambda + 96 = 0\) A1
\(\lambda = 8,12\) A1
first eigenvector satisfies
\(\left( {\begin{array}{*{20}{c}}
3&{\sqrt 3 }\\
{\sqrt 3 }&1
\end{array}} \right)\left( \begin{array}{l}
x\\
y
\end{array} \right) = \left( \begin{array}{l}
0\\
0
\end{array} \right)\) M1
\(\left( \begin{array}{l}
x\\
y
\end{array} \right) = \) (any multiple of) \(\left( {\begin{array}{*{20}{c}}
1\\
{ – \sqrt 3 }
\end{array}} \right)\) A1
second eigenvector satisfies
\(\left( {\begin{array}{*{20}{c}}
{ – 1}&{\sqrt 3 }\\
{\sqrt 3 }&{ – 3}
\end{array}} \right)\left( \begin{array}{l}
x\\
y
\end{array} \right) = \left( \begin{array}{l}
0\\
0
\end{array} \right)\)
\(\left( \begin{array}{l}
x\\
y
\end{array} \right) = \) (any multiple of ) \(\left( {\begin{array}{*{20}{c}}
{\sqrt 3 }\\
1
\end{array}} \right)\) A1
[7 marks]
(i) consider the rotation in which \((x,y)\) is transformed onto \((x’,y’)\) defined by
\(\left( \begin{array}{l}
{x’}\\
{y’}
\end{array} \right) = \left( {\begin{array}{*{20}{c}}
{\frac{1}{2}}&{ – \frac{{\sqrt 3 }}{2}}\\
{\frac{{\sqrt 3 }}{2}}&{\frac{1}{2}}
\end{array}} \right)\left( \begin{array}{l}
x\\
y
\end{array} \right)\) so that \(\left( \begin{array}{l}
x\\
y
\end{array} \right) = \left( {\begin{array}{*{20}{c}}
{\frac{1}{2}}&{\frac{{\sqrt 3 }}{2}}\\
{ – \frac{{\sqrt 3 }}{2}}&{\frac{1}{2}}
\end{array}} \right)\left( \begin{array}{l}
{x’}\\
{y’}
\end{array} \right)\) M1A1
the ellipse \(E\) becomes
\(\left( {\begin{array}{*{20}{c}}
{x’}&{y’}
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
{\frac{1}{2}}&{ – \frac{{\sqrt 3 }}{2}}\\
{\frac{{\sqrt 3 }}{2}}&{\frac{1}{2}}
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
{11}&{\sqrt 3 }\\
{\sqrt 3 }&9
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
{\frac{1}{2}}&{\frac{{\sqrt 3 }}{2}}\\
{ – \frac{{\sqrt 3 }}{2}}&{\frac{1}{2}}
\end{array}} \right)\left( \begin{array}{l}
{x’}\\
{y’}
\end{array} \right) = 24\) M1A1
\(\left( {\begin{array}{*{20}{c}}
{x’}&{y’}
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
8&0\\
0&{12}
\end{array}} \right)\left( \begin{array}{l}
{x’}\\
{y’}
\end{array} \right) = 24\) A1
\(2{(x’)^2} + 3{(y’)^2} = 6\) AG
(ii) the angle of rotation is given by \(\cos \theta = \frac{1}{2},\sin \theta = \frac{{\sqrt 3 }}{2}\) M1
since a rotational matrix has the form \(\left( {\begin{array}{*{20}{c}}
{\cos \theta }&{ – \sin \theta }\\
{\sin \theta }&{\cos \theta }
\end{array}} \right)\)
so \(\theta = {60^ \circ }\) (anticlockwise) A1
[7 marks]
Question
Consider the matrix M = \(\left[ {\begin{array}{*{20}{c}}
2 \\
{ – 1}
\end{array}\,\,\,\begin{array}{*{20}{c}}
{ – 4} \\
{ – 1}
\end{array}} \right]\).
a.Show that the linear transformation represented by M transforms any point on the line \(y = x\) to a point on the same line.[2]
b.Explain what happens to points on the line \(4y + x = 0\) when they are transformed by M.[3]
c.State the two eigenvalues of M.[2]
d.State two eigenvectors of M which correspond to the two eigenvalues.[2]
▶️Answer/Explanation
Markscheme
\(\left( {\begin{array}{*{20}{c}}
2 \\
{ – 1}
\end{array}\,\,\,\begin{array}{*{20}{c}}
{ – 4} \\
{ – 1}
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
k \\
k
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
{ – 2k} \\
{ – 2k}
\end{array}} \right)\left( { = – 2\left( {\begin{array}{*{20}{c}}
k \\
k
\end{array}} \right)} \right)\) M1A1
hence still on the line \(y = x\) AG
[2 marks]
consider \(\left( {\begin{array}{*{20}{c}}
2 \\
{ – 1}
\end{array}\,\,\,\begin{array}{*{20}{c}}
{ – 4} \\
{ – 1}
\end{array}} \right)\left( {\begin{array}{*{20}{c}}
{4k} \\
{ – k}
\end{array}} \right)\) M1
\( = \left( {\begin{array}{*{20}{c}}
{12k} \\
{ – 3k}
\end{array}} \right)\left( { = 3\left( {\begin{array}{*{20}{c}}
{4k} \\
{ – k}
\end{array}} \right)} \right)\) A1
hence the line is invariant A1
[3 marks]
hence the eigenvalues are −2 and 3 A1A1
[2 marks]
\(\left( {\begin{array}{*{20}{c}}
1 \\
1
\end{array}} \right)\) and \(\left( {\begin{array}{*{20}{c}}
4 \\
{ – 1}
\end{array}} \right)\) or equivalent A1A1
[2 marks]