Question
4. Karl has three brown socks and four black socks in his drawer. He takes two socks at random
from the drawer.
(a) Complete the tree diagram.
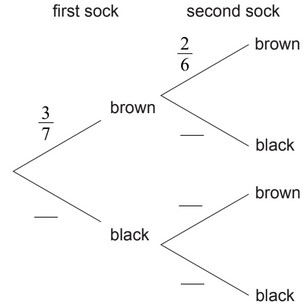
(b) Find the probability that Karl takes two socks of the same colour.
(c) Given that Karl has two socks of the same colour find the probability that he has two
brown socks.
▶️Answer/Explanation
Ans:
(a) 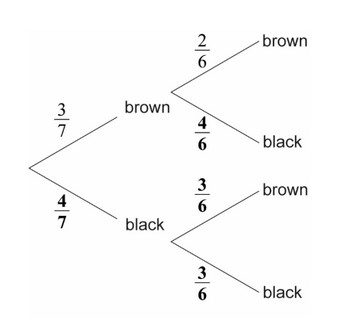
(b) multiplying along branches and then adding outcomes
\(\frac{3}{7} \times \frac{2}{6} + \frac{4}{7} \times \frac{3}{6}\)
\(=\frac{18}{42} (= \frac{3}{7} \approx 0.429 (42.9 %))\)
(c) use of conditional probability formula
\(\frac{(\frac{3}{7} \times \frac{2}{6})}{(\frac{3}{7})}\)
\(=\frac{6}{18} (=\frac{1}{3}) (\frac{252}{756}, 0.333, 33.3%)\)
Question
The following diagram shows the graph G .
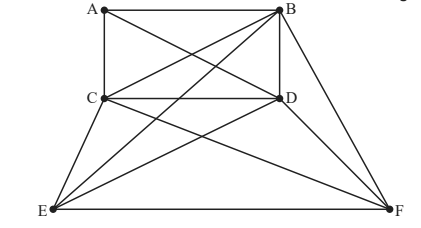
Verify that G satisfies the handshaking lemma. [3]
Show that G cannot be redrawn as a planar graph. [3]
State, giving a reason, whether G contains an Eulerian circuit. [2]
▶️Answer/Explanation
Ans:
(a)
METHOD 1
sum of degrees of vertices = 3 + 5 + 5 + 5 + 4 + 4 = 26 number of edges e = 13
the sum is equal to twice the number of edges which verifies the handshaking lemma
METHOD 2
degrees of vertices = 3,5,5,5,4,4there are 4 vertices of odd order there is an even number of vertices of odd order which verifies the handshaking lemma
(b) if planar then e ≤ 3v – 6 e = 13, v = 6 inequality not satisfied therefore G is not planar
(c) there are vertices of odd degree hence it does not contain an Eulerian circuit
Question
G is a simple, connected, planar graph with 9 vertices and e edges.
(a) Find the maximum possible value of e . [2]
The complement of G has e , edges.
(b) Find an expression for e , in terms of e . [2]
(c) Given that the complement of G is also planar and connected, find the possible values of e . [2]
H is a simple graph with v vertices and e edges.
(d) Given that both H and its complement are planar and connected, find the maximum possible value of v . [5]
▶️Answer/Explanation
Ans:
(a)
substitutes v=9 into either e = 3v-6 or \(e\leq 3v-6\) the maximum number of edges is 21 (e ≤ 21)
(b)
\(k_{9}\) has\( (_{2}^{9}=)\)36 edges
so \(e = 36-e (=(_{2}^{9})-e)\)
(c)
e’\( \leq 21\Rightarrow 36 – e \leq 21\)
\(15 \leq e \leq21\) (the possible values are 15,16,17,18,19,20,and 21)
(d)
recognises that \(e+e = \frac{v(v-1)}{2}\)(or equivalent)
uses \( e\leq 3v-6 \)and \(e\leq 3v-6\)
to form \(\frac{v(v-1)}{2}-(3v-6)\leq 3v-6\)
attempts to solve their quadratic inequality (equality)
\(v^{2}-13v+24\leq 0\Rightarrow 2.228…\leq v\leqslant 10.77…\)
the maximum possible value of v is \(10 (v\leq 10)\)
Question
a.A graph has n vertices with degrees 1, 2, 3, …, n. Prove that \(n \equiv 0(\bmod 4)\) or \(n \equiv 3(\bmod 4)\).[6]
b.Let G be a simple graph with n vertices, \(n \geqslant 2\). Prove, by contradiction, that at least two of the vertices of G must have the same degree.[8]
▶️Answer/Explanation
Markscheme
as each edge contributes 1 to each of the vertices that it is incident with, each edge will contribute 2 to the sum of the degrees of all the vertices (R1)
so \(2e = \sum {{\text{degrees}}} \) (A1)
\(2e = \frac{{n(n + 1)}}{2}\) A1
\(4|n(n + 1)\) A1
n and n + 1 are coprime R1
Note: Accept equivalent reasoning e.g. only one of n and n + 1 can be even.
\(4|n{\text{ or }}4|n + 1\) A1
\(n \equiv 0(\bmod 4){\text{ or }}n \equiv 3(\bmod 4)\) AG
[6 marks]
since G is simple, the highest degree that a vertex can have is n – 1 R1
the degrees of the vertices must belong to the set \(S = \{ 0,{\text{ }}1,{\text{ }}2,{\text{ }} \ldots ,{\text{ }}n – 1\} \) A1
proof by contradiction
if no two vertices have the same degree, all n vertices must have different degrees R1
as there are only n different degrees in set S, the degrees must be precisely the n numbers 0, 1, 2, …, n – 1 R1
let the vertex with degree 0 be A, then A is not adjacent to any of the other vertices R1
let the vertex with degree n – 1 be B, then B is adjacent to all of the other vertices including A R1R1
this is our desired contradiction, so there must be two vertices of the same degree R1
[8 marks]
Examiners report
Only the top candidates were able to produce logically, well thought-out proofs.
Only the top candidates were able to produce logically, well thought-out proofs.
