Question 4. [Maximum mark: 18]
In a small village there are two doctors’ clinics, one owned by Doctor Black and the other owned by Doctor Green. It was noted after each year that 3.5 % of Doctor Black’s patients moved to Doctor Green’s clinic and 5 % of Doctor Green’s patients moved to Doctor Black’s clinic. All additional losses and gains of patients by the clinics may be ignored.
At the start of a particular year, it was noted that Doctor Black had 2100 patients on their register, compared to Doctor Green’s 3500 patients.
a. Write down a transition matrix T indicating the annual population movement between clinics. [2]
b. Find a prediction for the ratio of the number of patients Doctor Black will have, compared to Doctor Green, after two years. [2]
c. Find a matrix P , with integer elements, such that T = PDP–1 , where D is a diagonal matrix.
d. Hence, show that the long-term transition matrix T x is given by T x =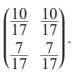 
e. Hence, or otherwise, determine the expected ratio of the number of patients Doctor Black would have compared to Doctor Green in the long term. [2]
▶️Answer/Explanation
(a) 
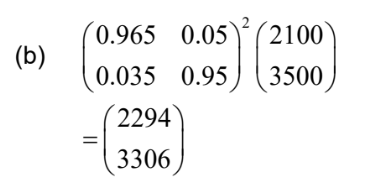so ratio is \(2294 : 3306 = (1147 :1653, 0.693889…)\)
(c) to solve Ax = λx :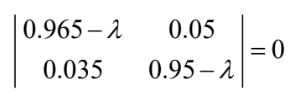 
\( (0.965 – λ) (0.95 – λ) -0.05 × 0.035 = 0\)
\(λ = 0.915 OR λ =1\)
attempt to find eigenvectors for at least one eigenvalue when \(λ = 0.915\) , \(x=(_{-1}^{1})\)
(or any real multiple) when λ =1, \(x=(_{7}^{10})\) therefore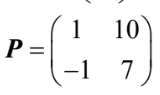 
(accept integer valued multiples of their eigenvectors and columns in either order) 
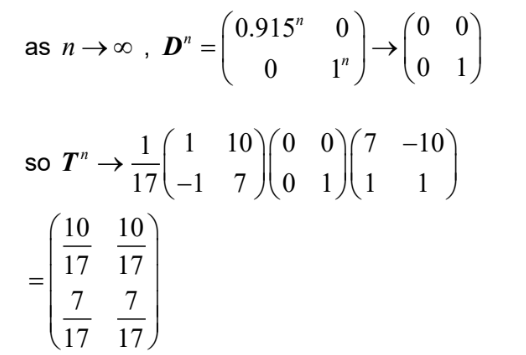
(e)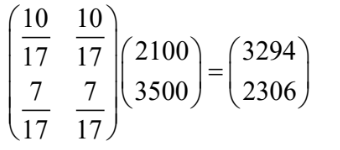 
so ratio is \(3294 : 2306\) \((1647 :1153, 1.42844…, 0.700060…)\)
Question 5. [Maximum mark: 13]
Long term experience shows that if it is sunny on a particular day in Vokram, then the probability that it will be sunny the following day is 0.8. If it is not sunny, then the probability that it will be sunny the following day is 0.3.
The transition matrix T is used to model this information, where T =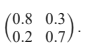 
a. It is sunny today. Find the probability that it will be sunny in three days’ time. [2]
b. Find the eigenvalues and eigenvectors of T . [5]
The matrix T can be written as a product of three matrices, PD P -1, where D is a diagonal matrix.
c.(i) Write down the matrix P .
c.(ii) Write down the matrix D . [2]
d. Hence find the long-term percentage of sunny days in Vokram. [4]
▶️Answer/Explanation
(a) finding T3 OR use of tree diagram T3 = 
the probability of sunny in three days’ time is 0.65
(b) attempt to find eigenvalues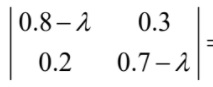 
\(= (0.8 \lambda )(0.7-\lambda )-0.06 = 0\) (\lambda ^{2}- 1.5 \lambda + 0.5= 0 \lambda =1, \lambda = 0.5)\)
attempt to find either eigenvector \(0.8+0.3y= x ⇒ -0.2x+ 0.3y= 0\) so an eigenvector is \((_{2}^{3})\)0.8x+ 0.3y = 0.5x ⇒ 0.3x+0.3y = 0\) so an eigenvector is \( _{1}^{-1}\)
(c) (i) P=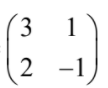 
OR P =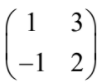 
(ii) D =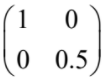 
OR D =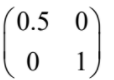 
(d) \(0.5n → 0\)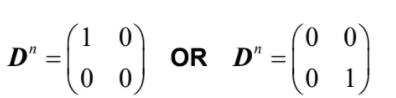 
PDnP-1 60 %
Question
A geneticist uses a Markov chain model to investigate changes in a specific gene in a cell
as it divides. Every time the cell divides, the gene may mutate between its normal state and
other states.
The model is of the form
\(\binom{X_{n+1}}{Z_{n+1}}=M\binom{X_{n}}{Z_{n}}\)
where Xn is the probability of the gene being in its normal state after dividing for the nth time,
and Zn is the probability of it being in another state after dividing for the nth time, where n∈ℕ.
Matrix M is found to be \(\begin{pmatrix}0.94 & b \\ 0.06 & 0.98\end{pmatrix}\)
(a) (i) Write down the value of b.
(ii) What does b represent in this context? [2]
(b) Find the eigenvalues of M. [3]
(c) Find the eigenvectors of M. [3]
(d) The gene is in its normal state when n = 0. Calculate the probability of it being in its
normal state
(i) when n = 5;
(ii) in the long term. [4]
▶️Answer/Explanation
Ans
5. (a) (i) 0.02 A1
(ii) the probability of mutating from ‘not normal state’ to ‘normal state’ A1
Note: The A1 can only be awarded if it is clear that transformation is from the mutated state.
[2 marks]
(b) \(det\begin{pmatrix}0.94-\lambda &0.02 \\ 0.06 & 0.98-\lambda \end{pmatrix}=0\) (M1)
Note: Award M1 for an attempt to find eigenvalues. Any indication that
det ( M − λI ) = 0 has been used is sufficient for the (M1).
(0.94− λ )(0.98 − λ) − 0.0012 = 0 OR λ2 −1.92 λ + 0.92 =0 (A1)
λ =1, 0.92 \(\left ( \frac{23}{25} \right )\) A1
[3 marks]
(c) \(\begin{pmatrix}0.94 &0.02 \\0.06 &0.98 \end{pmatrix}\binom{x}{y}=\binom{x}{y}\ OR \ \begin{pmatrix}0.94 &0.02 \\ 0.06 &0.98 \end{pmatrix}\binom{x}{y}=0.92\binom{x}{y}\) (M1)
Note: This M1 can be awarded for attempting to find either eigenvector.
0.02 y − 0.06 x = 0 OR 0.02 y + 0.02 x = 0
\(\binom{1}{3}and\binom{1}{-1}\) A1A1
Note: Accept any multiple of the given eigenvectors.
[3 marks]
(d) (i) \(\begin{pmatrix}0.94 &0.02 \\0.06 &0.98 \end{pmatrix}^{5}\binom{1}{0}\ OR \ \begin{pmatrix}0.744 &0.0852 \\ 0.256 &0.915 \end{pmatrix} \binom{1}{0}\) (M1)
Note: Condone omission of the initial state vector for the M1.
0.744 (0.744311…) A1
(ii) \(\begin{pmatrix}0.25\\0.75 \end{pmatrix}\) (A1)
Note: Award A1 for \(\begin{pmatrix}0.25\\0.75 \end{pmatrix}\) OR \(\begin{pmatrix}0.25 &0.25 \\ 0.75 & 0.75\end{pmatrix}\) seen
0.25 A1
[4 marks]
Total [12 marks]
Question
An automatic machine is used to fill bottles of water. The amount delivered, \(Y\) ml , may be assumed to be normally distributed with mean \(\mu \) ml and standard deviation \(8\) ml . Initially, the machine is adjusted so that the value of \(\mu \) is \(500\). In order to check that the value of \(\mu \) remains equal to \(500\), a random sample of 10 bottles is selected at regular intervals, and the mean amount of water, \(\overline y \) , in these bottles is calculated. The following hypotheses are set up.
\({{\rm{H}}_0}:\mu = 500\) ; \({{\rm{H}}_1}:\mu \ne 500\)
The critical region is defined to be \(\left( {\overline y < 495} \right) \cup \left( {\overline y > 505} \right)\) .
(i) Find the significance level of this procedure.
(ii) Some time later, the actual value of \(\mu \) is \(503\). Find the probability of a Type II error.
▶️Answer/Explanation
Markscheme
(i) Under \({{\rm{H}}_0}\) , the distribution of \({\overline y }\) is N(500, 6.4) . (A1)
Significance level \( = {\rm{P}}\overline y < 495\) or \( > 505|{{\rm{H}}_0}\) M2
\( = 2 \times 0.02405\) (A1)
\( = 0.0481\) A1 N5
Note: Using tables, answer is \(0.0478\).
(ii) The distribution of \(\overline y \) is now N(\(503\), \(6.4\)) . (A1)
P(Type ΙΙ error) \( = {\rm{P}}(495 < \overline y < 505)\) (M1)
\( = 0.785\) A1 N3
Note: Using tables, answer is \(0.784\).
[8 marks]
Question
A machine fills containers with grass seed. Each container is supposed to weigh \(28\) kg. However the weights vary with a standard deviation of \(0.54\) kg. A random sample of \(24\) bags is taken to check that the mean weight is \(28\) kg.
A.a.Assuming the series for \({{\rm{e}}^x}\) , find the first five terms of the Maclaurin series for\[\frac{1}{{\sqrt {2\pi } }}{{\rm{e}}^{\frac{{ – {x^2}}}{2}}} {\rm{ .}}\][3]
A.b.(i) Use your answer to (a) to find an approximate expression for the cumulative distributive function of \({\rm{N}}(0,1)\) .
(ii) Hence find an approximate value for \({\rm{P}}( – 0.5 \le Z \le 0.5)\) , where \(Z \sim {\rm{N}}(0,1)\) .[6]
B.a.State and justify an appropriate test procedure giving the null and alternate hypotheses.[5]
B.b.What is the critical region for the sample mean if the probability of a Type I error is to be \(3.5\%\)?[7]
B.c.If the mean weight of the bags is actually \(28\).1 kg, what would be the probability of a Type II error?[2]
▶️Answer/Explanation
Markscheme
\({{\rm{e}}^x} = 1 + x + \frac{{{x^2}}}{{2!}} + \frac{{{x^3}}}{{3!}} + \frac{{{x^4}}}{{4!}} + \ldots \)
\({{\rm{e}}^{\frac{{ – {x^2}}}{2}}} = 1 + \left( { – \frac{{{x^2}}}{2}} \right) + \frac{{{{\left( { – \frac{{{x^2}}}{2}} \right)}^2}}}{{2!}} + \frac{{{{\left( { – \frac{{{x^2}}}{2}} \right)}^3}}}{{3!}} + \frac{{{{\left( { – \frac{{{x^2}}}{2}} \right)}^4}}}{{4!}} + \ldots \) M1A1
\(\frac{1}{{\sqrt {2\pi } }}{{\rm{e}}^{\frac{{ – {x^2}}}{2}}} = \frac{1}{{\sqrt {2\pi } }}\left( {1 – \frac{{{x^2}}}{2} + \frac{{{x^4}}}{8} – \frac{{{x^6}}}{{48}} + \frac{{{x^8}}}{{384}}} \right)\) A1
[3 marks]
(i) \(\frac{1}{{\sqrt {2\pi } }}\int_0^x {1 – \frac{{{t^2}}}{2}} + \frac{{{t^4}}}{8} – \frac{{{t^6}}}{{48}} + \frac{{{t^8}}}{{384}}{\rm{d}}t\) M1
\( = \frac{1}{{\sqrt {2\pi } }}\left( {x – \frac{{{x^3}}}{6} + \frac{{{x^5}}}{{40}} – \frac{{{x^7}}}{{336}} + \frac{{{x^9}}}{{3456}}} \right)\) A1
\({\rm{P}}(Z \le x) = 0.5 + \frac{1}{{\sqrt {2\pi } }}\left( {x – \frac{{{x^3}}}{6} + \frac{{{x^5}}}{{40}} – \frac{{{x^7}}}{{336}} + \frac{{{x^9}}}{{3456}} – \ldots } \right)\) R1A1
(ii) \({\rm{P}}( – 0.5 \le Z \le 0.5) = \frac{2}{{\sqrt {2\pi } }}\left( {0.5 – \frac{{{{0.5}^3}}}{6} + \frac{{{{0.5}^5}}}{{40}} – \frac{{{{0.5}^7}}}{{336}} + \frac{{{{0.5}^9}}}{{3456}} – \ldots } \right)\) M1
\( = 0.38292 = 0.383\) A1
[6 marks]
this is a two tailed test of the sample mean \(\overline x \)
we use the central limit theorem to justify assuming that R1
\(\overline X \sim {\rm{N}}\left( {28,\frac{{{{0.54}^2}}}{{24}}} \right)\) R1A1
\({{\rm{H}}_0}:\mu = 28\) A1
\({{\rm{H}}_1}:\mu \ne 28\) A1
[5 marks]
since \({\text{P(Type I error)}} = 0.035\) , critical value \(2.108\) (M1)A1
and (\(\overline x \le 28 – 2.108\sqrt {\frac{{{{0.54}^2}}}{{24}}} \) or \(\overline x \ge 28 + 2.108\sqrt {\frac{{{{0.54}^2}}}{{24}}} \) ) (M1)(A1)(A1)
\(\overline x \le 27.7676\) or \(\overline x \ge 28.2324\)
so \(\overline x \le 27.8\) or \(\overline x \ge 28.2\) A1A1
[7 marks]
if \(\mu = 28.1\)
\(\overline X \sim {\rm{N}}\left( {28.1,\frac{{{{0.54}^2}}}{{24}}} \right)\) R1
\({\text{P(Type II error)}} = {\rm{P}}(27.7676 < \overline x < 28.2324)\)
\( = 0.884\) A1
Note: Depending on the degree of accuracy used for the critical region the answer for part (c) can be anywhere from \(0.8146\) to \(0.879\).
[2 marks]