Question 7. [Maximum mark: 17]
Consider the following system of coupled differential equations.
\(\frac{dx}{dt}\)= −4x
\(\frac{dx}{dt}\)= 3x − 2y
a. Find the eigenvalues and corresponding eigenvectors of the matrix 
[6]
b. Hence, write down the general solution of the system. [2]
c. Determine, with justification, whether the equilibrium point (0, 0) is stable or unstable. [2]
d. Find the value of \(\frac{dy}{dx}\)
(i) at (4 , 0).
(ii) at (−4, 0). [3]
e. Sketch a phase portrait for the general solution to the system of coupled differential equations for −6 ≤ x ≤ 6, −6 ≤ y ≤ 6. [4]
▶️Answer/Explanation
(a)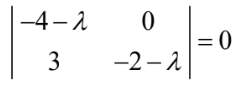 
\( (-4-\lambda )(-2-\lambda )=0\)
\(\lambda =-4\) OR \(\lambda =-2 \)
\(\lambda =-4\)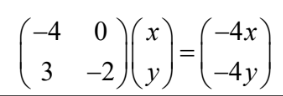 
\(3x-2y=-4y\)
\(3x=-2y\)
possible eigenvector is \((_{3}^{-2})(or any real multiple) \lambda =-2\)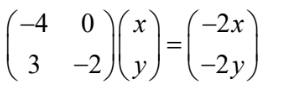 
\(x = 0, y = 1\) possible eigenvector is \((_{1}^{0}) (or any real multiple)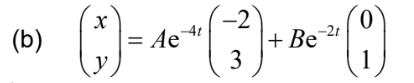 
(c) two (distinct) real negative eigenvalues (or equivalent (eg both \(e^{-4t}\rightarrow 0,e^{-2t}\rightarrow 0 as t\rightarrow \)∞ ⇒ stable equilibrium point
(d)\(\frac{dy}{dx}=\frac{3x-2y}{-4x}(i)(4,0)\Rightarrow \frac{dy}{dx}=-\frac{3}{4}(ii)(-4,0)\Rightarrow \frac{dy}{dx}=-\frac{3}{4}\)
(e)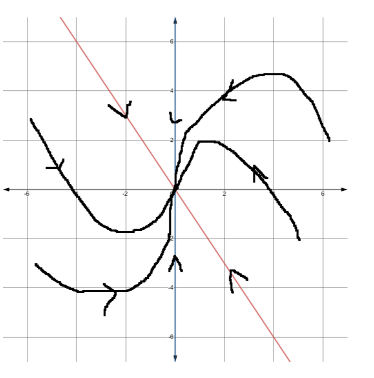 
Question 5. [Maximum mark: 14]
Hank sets up a bird table in his garden to provide the local birds with some food. Hank notices that a specific bird, a large magpie, visits several times per month and he names him Bill. Hank models the number of times per month that Bill visits his garden as a Poisson distribution with mean 3.1.
a. Using Hank’s model, find the probability that Bill visits the garden on exactly four occasions during one particular month. [1]
b. Over the course of 3 consecutive months, find the probability that Bill visits the garden:
(i)on exactly 12 occasions.
(ii)during the first and third month only. [5]
c. Find the probability that over a 12-month period, there will be exactly 3 months when Bill does not visit the garden. [4]
After the first year, a number of baby magpies start to visit Hank’s garden. It may be assumed that each of these baby magpies visits the garden randomly and independently, and that the number of times each baby magpie visits the garden per month is modelled by a Poisson distribution with mean 2.1.
d. Determine the least number of magpies required, including Bill, in order that the probability of Hank’s garden having at least 30 magpie visits per month is greater than 0.2. [4]
▶️Answer/Explanation
(a) X1 ~ Po (3.1) P (X1 =4) = 0.173 (0.173349…)
(b) (i) X2 ~ Po (3 3.1) Po (9.3) P (X2 =12) = 0.0799 (0.0798950…) (ii) (P(X1 > 0)2 ×P (X1 = 0) 0.954952 × 0.04505 = 0.0411 (0.0410817…)
(c) P (X1 = 0) = 0.04505 X1 ~ B ( 12, 0.04505) = 0.0133 (0.013283….)
(d) METHOD ONE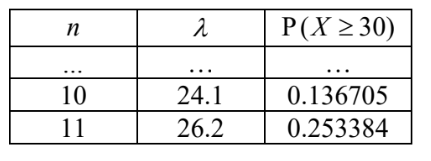 
so require 12 magpies (including Bill) METHOD TWO evidence of a cumulative Poisson with λ = 3.1 +2.1 l n sketch of curve and y = 0.2 (intersect at) 10.5810… rounding up gives n =11 so require 12 magpies (including Bill)
Question 7. [Maximum mark: 17]
A biologist introduces 100 rabbits to an island and records the size of their population (x) over a period of time. The population growth of the rabbits can be approximately modelled by the following differential equation, where t is time measured in years.
\(\frac{dx}{dt} = 2x\)
a. Find the population of rabbits 1 year after they were introduced. [5]
A population of 100 foxes is introduced to the island when the population of rabbits has reached 1000. The subsequent population growth of rabbits and foxes, where y is the population of foxes at time t , can be approximately modelled by the coupled equations:
\(\frac{dx}{dt}\) =x(2 – 0.01y)
\(\frac{dy}{dt}\) = y(0.0002x – 0.8)
b.Use Euler’s method with a step size of 0.25, to find
(i) the population of rabbits 1 year after the foxes were introduced.
(ii)the population of foxes 1 year after the foxes were introduced. [6]
c. The graph of the population sizes, according to this model, for the first 4 years after the foxes were introduced is shown below.
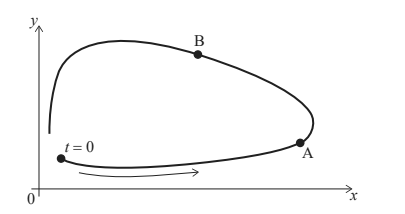
Describe the changes in the populations of rabbits and foxes for these 4 years at
(i)point A.
(ii)point B. [3]
d. find the non-zero equilibrium point for the populations of rabbits and foxes. [3]
▶️Answer/Explanation
(a) \(\int \frac{1}{x}dx=\int 2dt ln x =2t+c x= Ae^{2t}x(0)= 100 \Rightarrow A= 100 x = 100 e^{2t} x(1)739\)
(b) \(t_{n+1}=t _{n}+0.25 x_{n+1}\) = \(y _{n }+0.25y _{n }(2-0.01y_{n})x_{n+1}\) = \(y _{n }+0.25y _{n }(2-0.01y_{n}-0.8)\)
(i) 2840 (2836 OR 2837) (ii) 58 OR 59
(c) (i) both populations are increasing (ii) rabbits are decreasing and foxes are increasing
(d) setting at least one DE to zero x = 4000, y = 200
Question
A cafe makes x litres of coffee each morning. The cafe’s profit each morning, C, measured
in dollars, is modelled by the following equation
\(C=\frac{x}{10}\left ( k^{2}-\frac{3}{100}x^{2} \right )\)
where k is a positive constant.
(a) Find an expression for \(\frac{dC}{dx}\) in terms of k and x . [3]
(b) Hence find the maximum value of C in terms of k . Give your answer in the form pk3,
where p is a constant. [4]
The cafe’s manager knows that the cafe makes a profit of $426 when 20 litres of coffee are
made in a morning.
(c) (i) Find the value of k .
(ii) Use the model to find how much coffee the cafe should make each morning to
maximize its profit. [3]
(d) Sketch the graph of C against x , labelling the maximum point and the x-intercepts
with their coordinates. [3]
The manager of the cafe wishes to serve as many customers as possible.
(e) Determine the maximum amount of coffee the cafe can make that will not result in a
loss of money for the morning. [2]
▶️Answer/Explanation
Ans
2. (a) attempt to expand given expression OR attempt at product rule (M1)
\(C=\frac{xk^{2}}{10}-\frac{3x^{3}}{1000})
\(\frac{dC}{dx}=\frac{k^{2}}{10}-\frac{9x^{2}}{1000}\)
Note: Award M1 for power rule correctly applied to at least one term
and A1 for correct answer.
[3 marks]
(b) equating their \(\frac{dC}{dx}\) to zero (M1)
\(\frac{k^{2}}{10}-\frac{9x^{2}}{1000}=0\)
\(x^{2}=\frac{100k^{2}}{9}\)
\(x=\frac{10k}{3}\) (A1)
substituting their x back into given expression (M1)
\(C_{max}=\frac{10k}{30}\left ( k^{2}-\frac{300k^{2}}{900} \right )\)
\(C_{max}=\frac{2k}{9}\left ( 0.222…k^{3} \right )\) A1
[4 marks]
(c) (i) substituting 20 into given expression and equating to 426 M1
\(426=\frac{20}{10}\left ( k^{2}-\frac{3}{100}(20)^{2} \right )\)
k =15 A1
(ii) 50 A1
[3 marks]
continued
(d)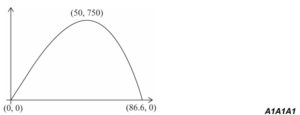 
Note: Award A1 for graph indicating an increasing and then decreasing function (drawn in first
quadrant), A1 for maximum labelled and A1 for graph drawn for positive x, passing
through the origin and 86.6 which is marked on the x-axis or its coordinates are given.
[3 marks]
(e) setting their expression for C to zero OR choosing correct x-intercept on
their graph of C (M1)
xmax = 86.6 (86.6025 ) … litres A1
[2 marks]
Total [15 marks]
Question
A cafe makes x litres of coffee each morning. The cafe’s profit each morning, C, measured
in dollars, is modelled by the following equation
\(C=\frac{x}{10}\left ( k^{2}-\frac{3}{100}x^{2} \right )\)
where k is a positive constant.
(a) Find an expression for \(\frac{dC}{dx}\) in terms of k and x . [3]
(b) Hence find the maximum value of C in terms of k . Give your answer in the form pk3,
where p is a constant. [4]
The cafe’s manager knows that the cafe makes a profit of $426 when 20 litres of coffee are
made in a morning.
(c) (i) Find the value of k .
(ii) Use the model to find how much coffee the cafe should make each morning to
maximize its profit. [3]
(d) Sketch the graph of C against x , labelling the maximum point and the x-intercepts
with their coordinates. [3]
The manager of the cafe wishes to serve as many customers as possible.
(e) Determine the maximum amount of coffee the cafe can make that will not result in a
loss of money for the morning. [2]
▶️Answer/Explanation
Ans
2. (a) attempt to expand given expression OR attempt at product rule (M1)
\(C=\frac{xk^{2}}{10}-\frac{3x^{3}}{1000})
\(\frac{dC}{dx}=\frac{k^{2}}{10}-\frac{9x^{2}}{1000}\)
Note: Award M1 for power rule correctly applied to at least one term
and A1 for correct answer.
[3 marks]
(b) equating their \(\frac{dC}{dx}\) to zero (M1)
\(\frac{k^{2}}{10}-\frac{9x^{2}}{1000}=0\)
\(x^{2}=\frac{100k^{2}}{9}\)
\(x=\frac{10k}{3}\) (A1)
substituting their x back into given expression (M1)
\(C_{max}=\frac{10k}{30}\left ( k^{2}-\frac{300k^{2}}{900} \right )\)
\(C_{max}=\frac{2k}{9}\left ( 0.222…k^{3} \right )\) A1
[4 marks]
(c) (i) substituting 20 into given expression and equating to 426 M1
\(426=\frac{20}{10}\left ( k^{2}-\frac{3}{100}(20)^{2} \right )\)
k =15 A1
(ii) 50 A1
[3 marks]
continued
(d)
Note: Award A1 for graph indicating an increasing and then decreasing function (drawn in first
quadrant), A1 for maximum labelled and A1 for graph drawn for positive x, passing
through the origin and 86.6 which is marked on the x-axis or its coordinates are given.
[3 marks]
(e) setting their expression for C to zero OR choosing correct x-intercept on
their graph of C (M1)
xmax = 86.6 (86.6025 ) … litres A1
[2 marks]
Total [15 marks]