Question 3. [Maximum mark: 16]
A new concert hall was built with 14 seats in the first row. Each subsequent row of the hall has two more seats than the previous row. The hall has a total of 20 rows.
a. Find:
(i) the number of seats in the last row.
(ii) the total number of seats in the concert hall. [5]
The concert hall opened in 2019. The average number of visitors per concert during that year was 584. In 2020, the average number of visitors per concert increased by 1.2 %.
b. Find the average number of visitors per concert in 2020. [2]
The concert organizers use this data to model future numbers of visitors. It is assumed that the average number of visitors per concert will continue to increase each year by 1.2 %.
c. Determine the first year in which this model predicts the average number of visitors per concert will exceed the total seating capacity of the concert hall. [5]
It is assumed that the concert hall will host 50 concerts each year.
d. Use the average number of visitors per concert per year to predict the total number of people expected to attend the concert hall from when it opens until the end of 2025. [4]
Answer/Explanation
(a) (i) recognition of arithmetic sequence with common difference 2
use of arithmetic sequence formula \(14 + 2(20 – 1) 52\)
(ii) use of arithmetic series formula \(\frac{14+52}{2}\times 20 600\)
(b) 584+ (584 × 0.012)OR 584 × (1.012)1591(591.008)
(c) METHOD 1
EITHER 660=584 (1.012)x-1 (x-1=)10.3(10.2559..)x= 11.3(11.2559..)2030
OR 660= 584(1.012)x x= 10.3 (10.2559..)2030
METHOD 2 11th term 658 (657.987…) 12th term 666 (665.883…) 2030
(d) 7 seen EITHER 584\((\frac{1.012^{7}-1}{1.012-1})\) multiplying their sum by 50 OR
sum of the number of visitors for their r and their seven years multiplying their sum by 50
OR 29200 \(\frac{(1.012^{7}-1)}{(1.012-1)}\)THEN
212000 (211907.3… ) Note: Follow though from their r from part (b).
Question
A large underground tank is constructed at Mills Airport to store fuel.
The tank is in the shape of an isosceles trapezoidal prism, ABCDEFGH .
AB = 70 m , AF = 200 m , AD = 40 m , BC = 40 m and CD = 110 m . Angle ADC = 60° and angle BCD = 60° . The tank is illustrated below.
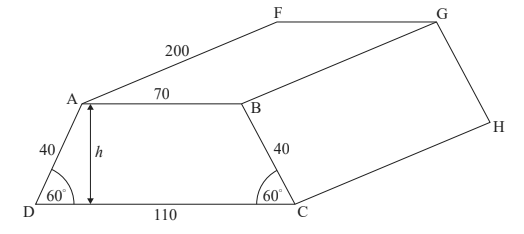
Find h , the height of the tank. [2]
Show that the volume of the tank is 624 000 m3, correct to three significant figures. [3]
Once construction was complete, a fuel pump was used to pump fuel into the empty tank. The amount of fuel pumped into the tank by this pump each hour decreases as an arithmetic sequence with terms u1 , u2 , u3 , … , un .
Part of this sequence is shown in the table.
Hour (n)
1st
2nd
3rd
…
Amount of fuel pumped into the tank in each hour, in m3 (un )
45 000
43 200
41 400
…
Write down the common difference, d . [1]
Find the amount of fuel pumped into the tank in the 13th hour. [2]
(i) Find the value of n such that un = 0 .
(ii) Write down the number of hours that the pump was pumping fuel into the tank. [3]
At the end of the 2nd hour, the total volume of fuel in the tank was 88 200 m3.
Find the total amount of fuel pumped into the tank in the first 8 hours. [2]
Show that the tank will never be completely filled using this pump. [3]
Answer/Explanation
Ans:
(a)
sin 60° = \(\frac{h}{40}\)
OR tan60 = \(\frac{h}{20} \)
\(OR 20^{2}+ h^{2}= 40 ^{2}(\sqrt{40^{2}-20^{2}})\)
(h=)34.6(m)\((\sqrt{1200,})20\sqrt{3}\),34.6410…
(b)
\(\frac{1}{2}(70+110)\)(34.6410…)\(\times 200\)
OR
\((2 \times \frac{1}{2}\times 20\times 34.6410…+70 \times 34.6410….)\)\(\times 200\)
OR
\(70\times 34.6410…\times 200+2\times \frac{1}{2}\times 34.6410…\times 20\times 200\)
623538…
624000 (cm3)
(c)
(d=)-1800
(d)
\((u_{13}=) 45000+ (13-1(-1800))\)
\(23400(m^{3})\)
(e)
(i)
0= 45000+ ((n-1)-1800))
(n=26)
(ii)25
(f)
\((S_{8})\frac{8}{2}(2\times 45000+(8-1)\times (-1800))\)
\(310000(m^{3})(3096000)\)
(g)
\((S_{25}=)\frac{25}{2}(2\times 45000+(25-)\times (-1800)),\)
\((S_{25=})\frac{25}{2}(45000+1800)\)
\((S_{25})= 585000 (m^{3})\)<624000 m3
OR
\(S_{n}= \frac{n}{2}(2\times 45000+(n-1)\times (-1800))\)
Maximum of this function 585225 (m3 )
585225(m3 ) < 624000(m3 ) hence it will never be filled
OR
sketch with concave down curve and labelled 624000 horizontal line
curve explicitly labelled as
\(s_{n}= \frac{n}{2}(2\times 450000+ (n-1)\times (-1800))\)or equivalent
the line and the curve do not intersect hence it will never be filled
OR
624000=\(\frac{n}{2}(2\times 45000+(n-1)\times (-1800))\)
Demonstrates there is no solution
There is no (real) solution (to this equation) hence it will never be filled
Question
The natural numbers: 1, 2, 3, 4, 5… form an arithmetic sequence.
A geometric progression \(G_1\) has 1 as its first term and 3 as its common ratio.
State the values of u1 and d for this sequence.[2]
Use an appropriate formula to show that the sum of the natural numbers from 1 to n is given by \(\frac{1}{2}n (n +1)\).[2]
Calculate the sum of the natural numbers from 1 to 200.[2]
The sum of the first n terms of G1 is 29 524. Find n.[3]
A second geometric progression G2 has the form \(1,\frac{1}{3},\frac{1}{9},\frac{1}{{27}}…\)[1]
Calculate the sum of the first 10 terms of G2.[2]
Explain why the sum of the first 1000 terms of G2 will give the same answer as the sum of the first 10 terms, when corrected to three significant figures.[1]
Using your results from parts (a) to (c), or otherwise, calculate the sum of the first 10 terms of the sequence \(2,3\frac{1}{3},9\frac{1}{9},27\frac{1}{{27}}…\)
Give your answer correct to one decimal place.[3]
Answer/Explanation
Markscheme
\(u_1 = d = 1\). (A1)(A1)[2 marks]
Sum is \(\frac{1}{2}n(2{u_1} + d(n – 1))\) or \(\frac{1}{2}n({u_1} + {u_n})\) (M1)
Award (M1) for either sum formula seen, even without substitution.
So sum is \(\frac{1}{2}n(2 + (n – 1)) = \frac{1}{2}n(n + 1)\) (A1)(AG)
Award (A1) for substitution of \({u_1} = 1 = d\) or \({u_1} = 1\) and \({u_n} = n\) with simplification where appropriate. \(\frac{1}{2}n(n + 1)\) must be seen to award this (A1).[2 marks]
\(\frac{1}{2}(200)(201) = 20 100\) (M1)(A1)(G2)
(M1) is for correct formula with correct numerical input. Original sum formula with u, d and n can be used.[2 marks]
\(\frac{{1 – {3^n}}}{{1 – 3}} = 29524\) (M1)(A1)
(M1) for correctly substituted formula on one side, (A1) for = 29524 on the other side.
n = 10. (A1)(G2)
Trial and error is a valid method. Award (M1) for at least \(\frac{{1 – {3^{10}}}}{{1 – 3}}\) seen and then (A1) for = 29524, (A1) for \(n = 10\). For only unproductive trials with \(n \ne 10\), award (M1) and then (A1) if the evaluation is correct.[3 marks]
Common ratio is \(\frac{1}{3}\), (0.333 (3sf) or 0.3) (A1)
Accept ‘divide by 3’.[1 mark]
\(\frac{{1 – {{\left( {\frac{1}{3}} \right)}^{10}}}}{{1 – \frac{1}{3}}}\) (M1)
= 1.50 (3sf) (A1)(ft)(G1)
1.5 and \(\frac{3}{2}\) receive (A0)(AP) if AP not yet used Incorrect formula seen in (a) or incorrect value in (b) can follow through to (c). Can award (M1) for \(1 + \left( {\frac{1}{3}} \right) + \left( {\frac{1}{9}} \right) + ……\)[2 marks]
Both \({\left( {\frac{1}{3}} \right)^{10}}\) and \({\left( {\frac{1}{3}} \right)^{1000}}\) (or those numbers divided by 2/3) are 0 when corrected to 3sf, so they make no difference to the final answer. (R1)
Accept any valid explanation but please note: statements which only convey the idea of convergence are not enough for (R1). The reason must show recognition that the convergence is adequately fast (though this might be expressed in a much less technical manner).[1 mark]
The sequence given is \(G_1 + G_2\) (M1)
The sum is 29 524 + 1.50 (A1)(ft)
= 29 525.5 (A1)(ft)(G2)
The (M1) is implied if the sum of the two numbers is seen. Award (G1) for 29 500 with no working. (M1) can be awarded for
\(2 + 3\frac{1}{3} + …\) Award final (A1) only for answer given correct to 1dp.[3 marks]
Question
Give all answers in this question correct to the nearest dollar.
Clara wants to buy some land. She can choose between two different payment options. Both options require her to pay for the land in 20 monthly installments.
Option 1: The first installment is \(\$ 2500\). Each installment is \(\$ 200\) more than the one before.
Option 2: The first installment is \(\$ 2000\). Each installment is \(8\% \) more than the one before.
If Clara chooses option 1,
(i) write down the values of the second and third installments;
(ii) calculate the value of the final installment;
(iii) show that the total amount that Clara would pay for the land is \(\$ 88000\).[7]
If Clara chooses option 2,
(i) find the value of the second installment;
(ii) show that the value of the fifth installment is \(\$ 2721\).[4]
The price of the land is \(\$ 80000\). In option 1 her total repayments are \(\$ 88000\) over the 20 months. Find the annual rate of simple interest which gives this total.[4]
Clara knows that the total amount she would pay for the land is not the same for both options. She wants to spend the least amount of money. Find how much she will save by choosing the cheaper option.[4]
Answer/Explanation
Markscheme
(i) Second installment \( = \$ 2700\) (A1)
Third installment \( = \$ 2900\) (A1)
(ii) Final installment \( = 2500 + 200 \times 19\) (M1)(A1)
Note: (M1) for substituting in correct formula or listing, (A1) for correct substitutions.
\( = \$ 6300\) (A1)(G2)
(iii) Total amount \( = \frac{{20}}{2}(2500 + 6300)\)
OR
\( \frac{{20}}{2}(5000 + 19 \times 200)\) (M1)(A1)
Note: (M1) for substituting in correct formula or listing, (A1) for correct substitution.
\( = \$ 88000\) (AG)
Note: Final line must be seen or previous (A1) mark is lost.[7 marks]
(i) Second installment \(2000 \times 1.08 = \$ 2160\) (M1)(A1)(G2)
Note: (M1) for multiplying by \(1.08\) or equivalent, (A1) for correct answer.
(ii) Fifth installment \( = 2000 \times {1.08^4} = 2720.98 = \$ 2721\) (M1)(A1)(AG)
Notes: (M1) for correct formula used with numbers from the problem. (A1) for correct substitution. The \(2720.9 \ldots \) must be seen for the (A1) mark to be awarded. Accept list of 5 correct values. If values are rounded prematurely award (M1)(A0)(AG).[4 marks]
Interest is \( = \$ 8000\) (A1)
\(80000 \times \frac{r}{{100}} \times \frac{{20}}{{12}} = 8000\) (M1)(A1)
Note: (M1) for attempting to substitute in simple interest formula, (A1) for correct substitution.
Simple Interest Rate \( = 6\% \) (A1)(G3)
Note: Award (G3) for answer of \(6\% \) with no working present if interest is also seen award (A1) for interest and (G2) for correct answer.[4 marks]
Financial accuracy penalty (FP) is applicable where indicated in the left hand column.
(FP) Total amount for option 2 \( = 2000\frac{{(1 – {{1.08}^{20}})}}{{(1 – 1.08)}}\) (M1)(A1)
Note: (M1) for substituting in correct formula, (A1) for correct substitution.
\( = \$ 91523.93\) (\( = \$ 91524\)) (A1)
\(91523.93 – 88000 = \$ 3523.93 = \$ 3524\) to the nearest dollar (A1)(ft)(G3)
Note: Award (G3) for an answer of \(\$ 3524\) with no working. The difference follows through from the sum, if reasonable. Award a maximum of (M1)(A0)(A0)(A1)(ft) if candidate has treated option 2 as an arithmetic sequence and has followed through into their common difference. Award a maximum of (M1)(A1)(A0)(ft)(A0) if candidate has consistently used \(0.08\) in (b) and (d).[4 marks]
Question
Throughout this question all the numerical answers must be given correct to the nearest whole number.
Park School started in January 2000 with \(100\) students. Every full year, there is an increase of \(6\% \) in the number of students.
Find the number of students attending Park School in
(i) January 2001;
(ii) January 2003.[4]
Park School started in January 2000 with \(100\) students. Every full year, there is an increase of \(6\% \) in the number of students.
Show that the number of students attending Park School in January 2007 is \(150\).[2]
Grove School had \(110\) students in January 2000. Every full year, the number of students is \(10\) more than in the previous year.
Find the number of students attending Grove School in January 2003.[2]
Grove School had \(110\) students in January 2000. Every full year, the number of students is \(10\) more than in the previous year.
Find the year in which the number of students attending Grove School will be first \(60\% \) more than in January 2000.[4]
Each January, one of these two schools, the one that has more students, is given extra money to spend on sports equipment.
(i) Decide which school gets the money in 2007. Justify your answer.
(ii) Find the first year in which Park School will be given this extra money.[5]
Answer/Explanation
Markscheme
(i) \(100 \times 1.06 = 106\) (M1)(A1)(G2)
Note: (M1) for multiplying by \(1.06\) or equivalent. (A1) for correct answer.
(ii) \(100 \times {1.06^3} = 119\) (M1)(A1)(G2)
Note: (M1) for multiplying by \({1.06^3}\) or equivalent or for list of values. (A1) for correct answer.[4 marks]
\(100 \times {1.06^7} = 150.36 \ldots = 150\) correct to the nearest whole (M1)(A1)(AG)
Note: (M1) for correct formula or for list of values. (A1) for correct substitution or for \(150\) in the correct position in the list. Unrounded answer must be seen for the (A1).[2 marks]
\(110 + 3 \times 10 = 140\) (M1)(A1)(G2)
Note: (M1) for adding \(30\) or for list of values. (A1) for correct answer.[2 marks]
In (d) and (e) follow through from (c) if consistent wrong use of correct AP formula.
\(110 + (n – 1) \times 10 > 176\) (A1)(M1)
\(n = 8\therefore {\text{year 2007}}\) (A1)(A1)(ft)(G2)
Note: (A1) for \(176\) or \(66\) seen. (M1) for showing list of values and comparing them to \(176\) or for equating formula to \(176\) or for writing the inequality. If \(n = 8\) not seen can still get (A2) for 2007. Answer \(n = 8\) with no working gets (G1).
OR
\(110 + n \times 10 > 176\) (A1)(M1)
\(n = 7\therefore {\text{year 2007}}\) (A1)(A1)(ft)(G2)[4 marks]
In (d) and (e) follow through from (c) if consistent wrong use of correct AP formula.
(i) \(180\) (A1)(ft)
Grove School gets the money. (A1)(ft)
Note: (A1) for \(180\) seen. (A1) for correct answer.
(ii) \({\text{100}} \times {\text{1}}{\text{.0}}{{\text{6}}^{n – 1}} > 110 + (n – 1) \times 10\) (M1)
\(n = 20\therefore {\text{year 2019}}\) (A1)(A1)(ft)(G2)
Note: (M1) for showing lists of values for each school and comparing them or for equating both formulae or writing the correct inequality. If \(n = 20\) not seen can still get (A2) for 2019. Follow through with ratio used in (b) and/or formula used in (d).
OR
\(100 \times {1.06^n} > 110 + n \times 10\) (M1)
\(n = 19\therefore {\text{year 2019}}\) (A1)(A1)(ft)(G2)
OR
graphically
Note: (M1) for sketch of both functions on the same graph, (A1) for the intersection point, (A1) for correct answer.[5 marks]
