Home / IB Mathematics SL 1.6 Approximation decimal places, significant figures AI SL Paper 2 – Exam Style Questions

IB Mathematics SL 1.6 Approximation decimal places, significant figures AI SL Paper 2 - Exam Style Questions - New Syllabus

IB DP Maths AI SL Paper 2 - All Topics

Question

Ishan recorded the number of daylight hours on the first day of each month in a northern-hemisphere city. This data was plotted onto a scatter diagram. The points were then joined by a smooth curve, with minimum point \((0,8)\) and maximum point \((6,16)\) as shown in the following diagram.

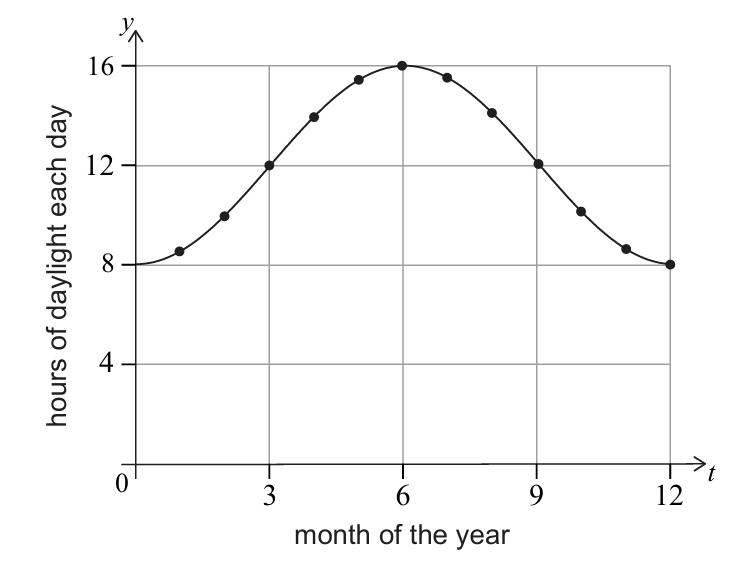
Let the curve in the diagram be \( y=f(t) \), where \( t \) is the time, measured in months, since Ishan first recorded these values. Ishan thinks that \( f(t) \) might be modelled by a quadratic function.

(a) Write down one reason why a quadratic function would not be a good model for the number of hours of daylight per day, across a number of years. [1]

Mira thinks that a better model is \( f(t)=a\cos(bt)+d,\ t\ge0 \), for specific values of \(a\), \(b\), and \(d\).

(b) For Mira’s model, use the diagram to write down:

(i) the amplitude.

(ii) the period.

(iii) the equation of the principal axis. [4]

(c) Hence or otherwise find the equation of this model in the form: [3]

\( f(t)=a\cos(bt)+d \)

(d) For the first year of the model, find the length of time when there are more than 10 hours and 30 minutes of daylight per day. [4]

The true maximum number of daylight hours was 16 hours and 14 minutes.

(e) Calculate the percentage error in the maximum number of daylight hours Ishan recorded in the diagram. [3]

▶️ Answer / Explanation
Solution

(a) Reason against quadratic model

A quadratic does not model a repeating annual cycle; over many years it would grow without bound or decrease indefinitely and cannot capture perpetual oscillations. (Any one valid reason earns the mark.) [1]

(b) Read from diagram

Minimum \(=8\), maximum \(=16\) at \(t=6\).
(i) Amplitude \(=\dfrac{16-8}{2}= \boxed{4}\).
(ii) Period \(=\boxed{12\text{ months}}\).
(iii) Principal axis \(y=\dfrac{16+8}{2}= \boxed{12}\). [4]

(c) Model parameters

Using cosine with a minimum at \(t=0\): \(f(t)=12-4\cos(30t^{\circ})\) (since \(360^{\circ}/\text{period}=360^{\circ}/12=30^{\circ}\) per month).
\(\boxed{f(t)=-4\cos(30t^{\circ})+12}\). [3]

(d) Time with > \(10.5\) hours

\( -4\cos(30t^{\circ})+12>10.5 \ \Rightarrow\ \cos(30t^{\circ})<0.375.\)
Let \(\theta=30t^{\circ}\). Then \(\theta\in\big(\arccos 0.375,\ 360^{\circ}-\arccos 0.375\big)\) within one year.
\(\arccos(0.375)\approx 67.98^{\circ}\). Duration (in degrees) \(=360^{\circ}-2\times 67.98^{\circ}=224.04^{\circ}\).
Convert to months: \(\Delta t=\dfrac{224.04^{\circ}}{30^{\circ}\!/\text{month}} \approx \boxed{7.47\ \text{months}}\) (to 3 s.f.). [4]

(e) Percentage error in maximum

Recorded maximum \(=16\) h; true maximum \(=16+\dfrac{14}{60}=16.233\overline{3}\) h.
\[
\text{Percentage error}
= \left|\frac{16-\left(16+\tfrac{14}{60}\right)}{16+\tfrac{14}{60}}\right|\times 100\%
\approx \boxed{1.44\%}.
\]
[3]
Total Marks: 15
More DP Math AI SL Paper 2 Questions..
Scroll to Top