Question
Cedric wants to buy an €8000 car. The car salesman offers him a loan repayment option of a 25 % deposit followed by 12 equal monthly payments of €600 .
Write down the amount of the deposit.[1]
Calculate the total cost of the loan under this repayment scheme.[2]
Cedric’s mother decides to help him by giving him an interest free loan of €8000 to buy the car. She arranges for him to repay the loan by paying her €x in the first month and €y in every following month until the €8000 is repaid.
The total amount that Cedric’s mother receives after 12 months is €3500. This can be written using the equation x +11y = 3500. The total amount that Cedric’s mother receives after 24 months is €7100.
Write down a second equation involving x and y.[1]
Cedric’s mother decides to help him by giving him an interest free loan of €8000 to buy the car. She arranges for him to repay the loan by paying her €x in the first month and €y in every following month until the €8000 is repaid.
The total amount that Cedric’s mother receives after 12 months is €3500. This can be written using the equation x +11y = 3500. The total amount that Cedric’s mother receives after 24 months is €7100.
Write down the value of x and the value of y.[2]
Cedric’s mother decides to help him by giving him an interest free loan of €8000 to buy the car. She arranges for him to repay the loan by paying her €x in the first month and €y in every following month until the €8000 is repaid.
The total amount that Cedric’s mother receives after 12 months is €3500. This can be written using the equation x +11y = 3500. The total amount that Cedric’s mother receives after 24 months is €7100.
Calculate the number of months it will take Cedric’s mother to receive the €8000.[3]
Cedric decides to buy a cheaper car for €6000 and invests the remaining €2000 at his bank. The bank offers two investment options over three years.
Option A: Compound interest at an annual rate of 8 %.
Option B: Compound interest at a nominal annual rate of 7.5 % , compounded monthly.
Express each answer in part (f) to the nearest euro.
Calculate the value of his investment at the end of three years if he chooses
(i) Option A;
(ii) Option B.[5]
Answer/Explanation
Markscheme
2000 (euros) (A1)[1 mark]
\(2000 + 12 \times 600\) (M1)
Note: Award (M1) for addition of two correct terms.
9200 (euros) (A1)(ft)(G2)
Note: Follow through from their part (a).[2 marks]
x + 23y = 7100 (A1)[1 mark]
x = 200, y = 300 (A1)(ft)(A1)(ft)(G2)[2 marks]
\(200 + n \times 300 = 8000\) (M1)
Note: Award (M1) for setting up the equation. Follow through from their x and y found in part (d).
n = 26 (A1)(ft)
26 + 1 = 27 (months) (A1)(ft)(G3)
Notes: Middle line n = 26 may be implied if correct answer given. The final (A1)(ft) is for adding 1 to their value of n (even if it is incorrect). Follow through from their part (d). If the final answer is not a positive integer award at most (M1)(A1)(ft)(A0). Award (G2) for final answer of 26.
OR
\(\frac{{8000 – 7100}}{{300}} + 24\) (M1)(A1)
Note: Award (M1) for division of difference by their value of y, (A1) for 24 seen.
27 (months) (A1)(ft)(G3)
Note: Follow through from their value of y.[3 marks]
(i) \(2000{\left( {1 + \frac{8}{{100}}} \right)^3}\) (M1)
Note: Award (M1) for correct substitution in compound interest formula.
2519 (euros) (A1)(G2)
Note: If the answer is not given to the nearest euro award at most (M1)(A0).(ii) \(2000{\left( {1 + \frac{7.5}{{100 \times 12}}} \right)^{3\times12}}\) (M1)(A1)
Note: Award (M1) for substitution in compound interest formula, (A1) for correct substitutions.
2503 (euros) (A1)(G2)
Note: If the answer is not given to the nearest euro, award at most (M1)(A1)(A0), provided this has not been penalized in part (f)(i).[5 marks]
Question
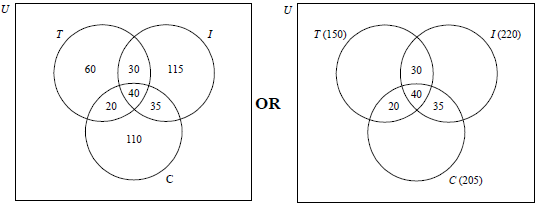
In a college 450 students were surveyed with the following results
150 have a television
205 have a computer
220 have an iPhone
75 have an iPhone and a computer
60 have a television and a computer
70 have a television and an iPhone
40 have all three.
Draw a Venn diagram to show this information. Use T to represent the set of students who have a television, C the set of students who have a computer and I the set of students who have an iPhone.[4]
Write down the number of students that
(i) have a computer only;
(ii) have an iPhone and a computer but no television.[2]
Write down \(n[T \cap (C \cup I)’]\).[1]
Calculate the number of students who have none of the three.[2]
Two students are chosen at random from the 450 students. Calculate the probability that
(i) neither student has an iPhone;
(ii) only one of the students has an iPhone.[6]
The students are asked to collect money for charity. In the first month, the students collect x dollars and the students collect y dollars in each subsequent month. In the first 6 months, they collect 7650 dollars. This can be represented by the equation x + 5y = 7650.
In the first 10 months they collect 13 050 dollars.
(i) Write down a second equation in x and y to represent this information.
(ii) Write down the value of x and of y .[3]
The students are asked to collect money for charity. In the first month, the students collect x dollars and the students collect y dollars in each subsequent month. In the first 6 months, they collect 7650 dollars. This can be represented by the equation x + 5y = 7650.
In the first 10 months they collect 13 050 dollars.
Calculate the number of months that it will take the students to collect 49 500 dollars.[3]
Answer/Explanation
Markscheme
 (A1)(A1)(A1)(A1)
(A1)(A1)(A1)(A1)
Notes: Award (A1) for labelled sets T, C, and I included inside an enclosed universal set. (Label U is not essential.) Award (A1) for central entry 40. (A1) for 20, 30 and 35 in the other intersecting regions. (A1) for 60, 110 and 115 or T(150), C(205), I(220).[4 marks]
In parts (b), (c) and (d) follow through from their diagram.
(i) 110 (A1)(ft)
(ii) 35 (A1)(ft)[2 marks]
In parts (b), (c) and (d) follow through from their diagram.
60 (A1)(ft)[2 marks]
In parts (b), (c) and (d) follow through from their diagram.
450 − (60 + 20 + 40 + 30 + 115 + 35 + 110) (M1)
Note: Award (M1) for subtracting all their values from 450.
= 40 (A1)(ft)(G2)[2 marks]
(i) \(\frac{{230}}{{450}} \times \frac{{229}}{{449}}\) (A1)(M1)
Note: Award (A1) for correct fractions, (M1) for multiplying their fractions.
\(\frac{{52670}}{{202050}}\left( {\frac{{5267}}{{20205}},{\text{ 0}}{\text{.261, 26}}{\text{.1% }}} \right)(0.26067…)\) (A1)(G2)
Note: Follow through from their Venn diagram in part (a).
(ii) \(\frac{{220}}{{450}} \times \frac{{230}}{{449}} + \frac{{230}}{{450}} \times \frac{{220}}{{449}}\) (A1)(A1)
Note: Award (A1) for addition of their products, (A1) for two correct products.
OR
\(\frac{{230}}{{450}} \times \frac{{220}}{{449}} \times 2\) (A1)(A1)
Notes: Award (A1) for their product of two fractions multiplied by 2, (A1) for correct product of two fractions multiplied by 2. Award (A0)(A0) if correct product is seen not multiplied by 2.
\(\frac{{2024}}{{4041}}(0.501,{\text{ 50}}{\text{.1% )(0}}{\text{.50086}}…{\text{)}}\) (A1)(G2)
Note: Follow through from their Venn diagram in part (a) and/or their 230 used in part (e)(i).
Note: For consistent use of replacement in parts (i) and (ii) award at most (A0)(M1)(A0) in part (i) and (A1)(ft)(A1)(A1)(ft) in part (ii).[6 marks]
(i) x + 9y = 13050 (A1)
(ii) x = 900 (A1)(ft)
y = 1350 (A1)(ft)
Notes: Follow through from their equation in (f)(i). Do not award (A1)(ft) if answer is negative. Award (M1)(A0) for an attempt at solving simultaneous equations algebraically but incorrect answer obtained.[3 marks]
49500 = 900 + 1350n (A1)(ft)
Notes: Award (A1)(ft) for setting up correct equation. Follow through from candidate’s part (f).
n = 36 (A1)(ft)
The total number of months is 37. (A1)(ft)(G2)
Note: Award (G1) for 36 seen as final answer with no working. The value of n must be a positive integer for the last two (A1)(ft) to be awarded.
OR
49500 = 900 + 1350(n − 1) (A2)(ft)
Notes: Award (A2)(ft) for setting up correct equation. Follow through from candidate’s part (f).
n = 37 (A1)(ft)(G2)
Note: The value of n must be a positive integer for the last (A1)(ft) to be awarded.[3 marks]
Question
A surveyor has to calculate the area of a triangular piece of land, DCE.
The lengths of CE and DE cannot be directly measured because they go through a swamp.
AB, DE, BD and AE are straight paths. Paths AE and DB intersect at point C.
The length of AB is 15 km, BC is 10 km, AC is 12 km, and DC is 9 km.
The following diagram shows the surveyor’s information.
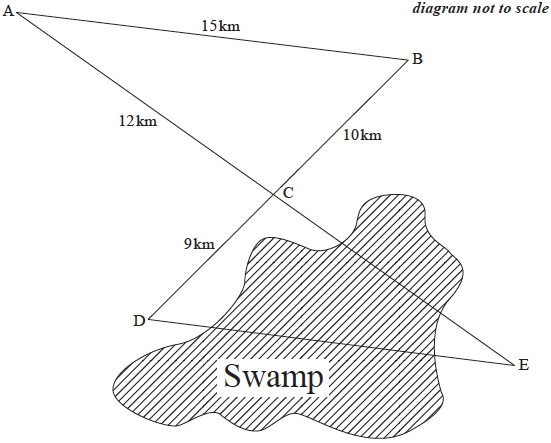
(i) Find the size of angle \({\rm{ACB}}\).
(ii) Show that the size of angle \({\rm{DCE}}\) is \(85.5^\circ\), correct to one decimal place.[4]
The surveyor measures the size of angle \({\text{CDE}}\) to be twice that of angle \({\text{DEC}}\).
(i) Using angle \({\text{DCE}} = 85.5^\circ \), find the size of angle \({\text{DEC}}\).
(ii) Find the length of \({\text{DE}}\).[5]
Calculate the area of triangle \({\text{DEC}}\).[4]
Answer/Explanation
Markscheme
(i) \(\cos {\rm{A\hat CB}} = \frac{{{{10}^2} + {{12}^2} – {{15}^2}}}{{2 \times 10 \times 12}}\) (M1)(A1)
Note: Award (M1) for substituted cosine rule,
(A1) for correct substitution.
\({\rm{A\hat CB}} = 85.5^\circ \;\;\;({\text{85.4593}} \ldots {\text{)}}\) (A1)(G2)
(ii) \({\rm{D\hat CE}} = {\rm{A\hat CB}}\;\;\;{\text{and}}\;\;\;{\rm{A\hat CB}} = 85.5^\circ \;\;\;({\text{85.4593}} \ldots ^\circ {\text{)}}\) (A1)
OR
\({\rm{B\hat CE}} = 180^\circ – 85.5^\circ = 94.5^\circ \;\;\;{\text{and}}\;\;\;{\rm{D\hat CE}} = 180^\circ – 94.5^\circ = 85.5^\circ \) (A1)
Notes: Both reasons must be seen for the (A1) to be awarded.
\({\rm{D\hat CE}} = 85.5^\circ \) (AG)
(i) \({\rm{D\hat EC}} = \frac{{180^\circ – 85.5^\circ }}{3}\) (M1)
\({\rm{D\hat EC}} = 31.5^\circ \) (A1)(G2)
(ii) \(\frac{{\sin (31.5^\circ )}}{9} = \frac{{\sin (85.5^\circ )}}{{{\text{DE}}}}\) (M1)(A1)(ft)
Note: Award (M1) for substituted sine rule, (A1) for correct substitution.
\({\text{DE}} = 17.2{\text{ (km)}}(17.1718 \ldots )\). (A1)(ft)(G2)
\(0.5 \times 17.1718 \ldots \times 9 \times \sin (63^\circ )\) (A1)(ft)(M1)(A1)(ft)
Note: Award (A1)(ft) for \(63\) seen, (M1) for substituted triangle area formula, (A1)(ft) for \(0.5 \times 17.1718 \ldots \times 9 \times \sin ({\text{their angle CDE}})\).
OR
\({\text{(triangle height}} = ){\text{ }}9 \times \sin (63^\circ )\) (A1)(ft)(A1)(ft)
\({\text{0.5}} \times {\text{17.1718}} \ldots \times {\text{9}} \times {\text{sin(their angle CDE)}}\) (M1)
Note: Award (A1)(ft) for \(63\) seen, (A1)(ft) for correct triangle height with their angle \({\text{CDE}}\), (M1) for \({\text{0.5}} \times {\text{17.1718}} \ldots \times {\text{9}} \times {\text{sin(their angle CDE)}}\).
\( = 68.9{\text{ k}}{{\text{m}}^2}\;\;\;(68.8509 \ldots )\) (A1)(ft)(G3)
Notes: Units are required for the last (A1)(ft) mark to be awarded.
Follow through from parts (b)(i) and (b)(ii).
Follow through from their angle \({\text{CDE}}\) within this part of the question.
Question
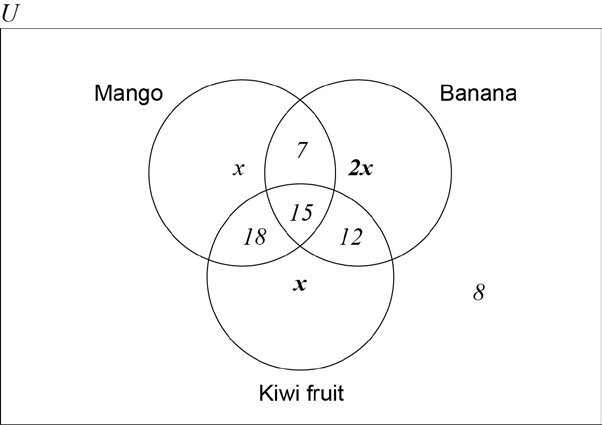
A group of 100 customers in a restaurant are asked which fruits they like from a choice of mangoes, bananas and kiwi fruits. The results are as follows.
15 like all three fruits
22 like mangoes and bananas
33 like mangoes and kiwi fruits
27 like bananas and kiwi fruits
8 like none of these three fruits
\(x\) like only mangoes
Copy the following Venn diagram and correctly insert all values from the above information.
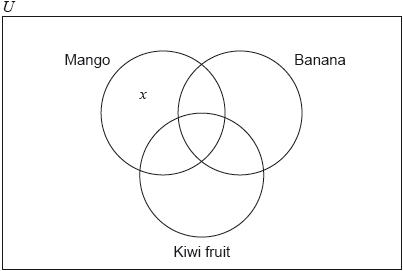 [3]
[3]
The number of customers that like only mangoes is equal to the number of customers that like only kiwi fruits. This number is half of the number of customers that like only bananas.
Complete your Venn diagram from part (a) with this additional information in terms of \(x\).[2]
The number of customers that like only mangoes is equal to the number of customers that like only kiwi fruits. This number is half of the number of customers that like only bananas.
Find the value of \(x\).[2]
The number of customers that like only mangoes is equal to the number of customers that like only kiwi fruits. This number is half of the number of customers that like only bananas.
Write down the number of customers who like
(i) mangoes;
(ii) mangoes or bananas.[2]
The number of customers that like only mangoes is equal to the number of customers that like only kiwi fruits. This number is half of the number of customers that like only bananas.
A customer is chosen at random from the 100 customers. Find the probability that this customer
(i) likes none of the three fruits;
(ii) likes only two of the fruits;
(iii) likes all three fruits given that the customer likes mangoes and bananas.[4]
The number of customers that like only mangoes is equal to the number of customers that like only kiwi fruits. This number is half of the number of customers that like only bananas.
Two customers are chosen at random from the 100 customers. Find the probability that the two customers like none of the three fruits.[3]
Answer/Explanation
Markscheme
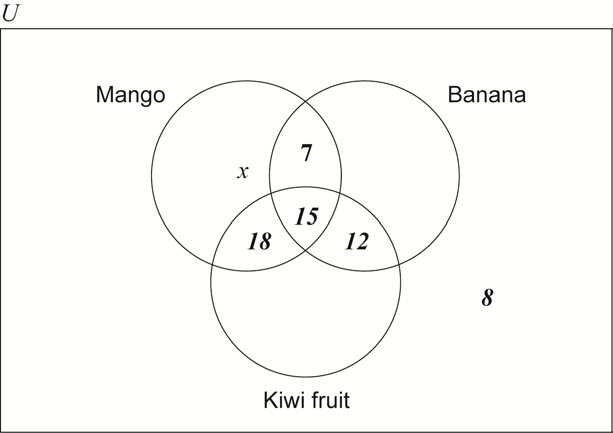 (A1)(A1)(A1)
(A1)(A1)(A1)
Notes: Award (A1) for 15 in the correct place.
Award (A1) for 7, 18 and 12 seen in the correct places.
Award (A1) for 8 in the correct place.
Award at most (A0)(A1)(A1) if diagram is missing the rectangle.
 (A1)(A1)
(A1)(A1)
Notes: Award (A1) for \(x\) seen in the correct places.
Award (A1) for \(2x\) seen in the correct place.
Award (A0)(A1)(ft) if \(x\) and \(2x\) are replaced by 10 and 20 respectively.
\(2x + x + x + 15 + 8 + 7 + 18 + 12 = 100\;\;\;(4x + 60 = 100{\text{ or equivalent)}}\) (M1)
Note: Award (M1) for equating the sum of the elements of their Venn diagram to \(100\). Equating to \(100\) may be implied.
\((x = ){\text{ }}10\) (A1)(ft)(G2)
Note: Follow through from their Venn diagram. The answer must be a positive integer.
(i) \(50\) (A1)(ft)
(ii) \(82\) (A1)(ft)
Note: Follow through from their answer to part (c) and their Venn diagram.
Award (A0)(ft)(A1)(ft) if answer is \(\frac{{50}}{{100}}\) and \(\frac{{82}}{{100}}\).
(i) \(\frac{8}{{100}}\;\;\;\left( {\frac{2}{{25}};{\text{ }}0.08;{\text{ }}8\% } \right)\) (A1)
Note: Correct answer only. There is no follow through.
(ii) \(\frac{{37}}{{100}}\;\;\;(0.37,{\text{ }}37\% )\) (A1)(ft)
Note: Follow through from their Venn diagram.
(iii) \(\frac{{15}}{{22}}\;\;\;(0.681;{\text{ }}0.682;{\text{ }}68.2\% )\;\;\;(0.681818 \ldots )\) (A1)(A1)(ft)(G2)
Notes: Award (A1) for numerator, (A1)(ft) for denominator, follow through from their Venn diagram. Award (A0)(A0) if answer is given as incorrect reduced fraction without working.
\(\frac{8}{{100}} \times \frac{7}{{99}}\) (A1)(ft)(M1)
Note: Award (A1)(ft) for correct fractions, follow through from their answer to part (e)(i), (M1) for multiplying their fractions.
\( = \frac{{56}}{{9900}}\;\;\;\left( {\frac{{14}}{{2477}},{\text{ }}0.00565656 \ldots ,{\text{ }}0.00566,{\text{ }}0.0056,{\text{ }}0.566\% } \right)\) (A1)(ft)(G2)
Question
The following table shows the number of bicycles, \(x\), produced daily by a factory and their total production cost, \(y\), in US dollars (USD). The table shows data recorded over seven days.
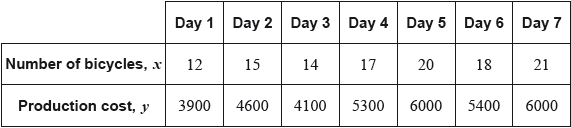
(i) Write down the Pearson’s product–moment correlation coefficient, \(r\), for these data.
(ii) Hence comment on the result.[4]
Write down the equation of the regression line \(y\) on \(x\) for these data, in the form \(y = ax + b\).[2]
Estimate the total cost, to the nearest USD, of producing \(13\) bicycles on a particular day.[3]
All the bicycles that are produced are sold. The bicycles are sold for 304 USD each.
Explain why the factory does not make a profit when producing \(13\) bicycles on a particular day.[2]
All the bicycles that are produced are sold. The bicycles are sold for 304 USD each.
(i) Write down an expression for the total selling price of \(x\) bicycles.
(ii) Write down an expression for the profit the factory makes when producing \(x\) bicycles on a particular day.
(iii) Find the least number of bicycles that the factory should produce, on a particular day, in order to make a profit.[5]
Answer/Explanation
Markscheme
(i) \(r = 0.985\;\;\;(0.984905 \ldots )\) (G2)
Notes: If unrounded answer is not seen, award (G1)(G0) for \(0.99\) or \(0.984\). Award (G2) for \(0.98\).
(ii) strong, positive (A1)(A1)
\(y = 259.909 \ldots x + 698.648 \ldots \;\;\;(y = 260x + 699)\) (G1)(G1)
Notes: Award (G1) for \(260x\) and (G1) for \(699\). If the answer is not an equation award a maximum of (G1)(G0).
\(y = 259.909 \ldots \times 13 + 698.648 \ldots \) (M1)
Note: Award (M1) for substitution of \(13\) into their regression line equation from part (b).
\(y = 4077.47 \ldots \) (A1)(ft)(G2)
\(y = 4077{\text{ (USD)}}\) (A1)(ft)
Notes: Follow through from their answer to part (b). If rounded values from part (b) used, answer is \(4079\). Award the final (A1)(ft) for a correct rounding to the nearest USD of their answer. The unrounded answer may not be seen.
If answer is \(4077\) and no working is seen, award (G2).
\(13 \times 304 – (4077.47) = – 125.477 \ldots \;\;\;( – 125)\;\;\;\)OR
\(4077.47 – (13 \times 304) = 125.477 \ldots \;\;\;(125)\) (M1)
Notes: Award (M1) for calculating the difference between \(13 \times 304\) and their answer to part (c).
If rounded values are used in equation, answer is \( – 127\).
profit is negative\(\;\;\;\)OR\(\;\;\;{\text{cost}} > {\text{sales}}\) (A1)
OR
\(13 \times 304 = 3952\) (M1)
Note: Award (M1) for calculating the price of \(13\) bikes.
\(3952 < 4077.47\) (A1)(ft)
Note: Award (A1) for showing \(3952\) is less than their part (c). This may be communicated in words. Follow through from part (c), but only if value is greater than \(3952\).
OR
\(\frac{{4077}}{{13}} = 313.62\) (M1)
Note: Award (M1) for calculating the cost of \(1\) bicycle.
\(313.62 > 304\) (A1)(ft)
Note: Award (A1) for showing \(313.62\) is greater than \(304\). This may be communicated in words. Follow through from part (c), but only if value is greater than \(304\).
OR
\(\frac{{4077}}{{304}} = 13.41\) (M1)
Note: Award (M1) for calculating the number of bicycles that should have been be sold to cover total cost.
\(13.41 > 13\) (A1)(ft)
Note: Award (A1) for showing \(13.41\) is greater than \(13\). This may be communicated in words. Follow through from part (c), but only if value is greater than \(13\).
(i) \(304x\) (A1)
(ii) \(304x – (259.909 \ldots x + 698.648 \ldots )\) (A1)(ft)(A1)(ft)
Note: Award (A1)(ft) for difference between their answers to parts (b) and (e)(i), (A1)(ft) for correct expression.
(iii) \(304x – (259.909 \ldots x + 698.648 \ldots ) > 0\) (M1)
Notes: Award (M1) for comparing their expression in part (e)(ii) to \(0\). Accept an equation. Accept \(3040x – y > 0\) or equivalent.
\(x = 16{\text{ bicycles}}\) (A1)(ft)(G2)
Notes: Follow through from their answer to part (b). Answer must be a positive integer greater than \(13\) for the (A1)(ft) to be awarded.
Award (G1) for an answer of \(15.84\).
